4. Функции одной переменной

4.1. Начальные определения. Терминология

Во вводной части нашего пособия было приведено общее определение функции. Далее речь пойдет о функциях, определенных на числовых множествах и принимающих числовые значения. Учитывая это, сформулируем определение такой функции и уточним некоторые детали.

Определение 4.1. Пусть и - два числовых множества, то есть , . Пусть по некоторому правилу каждому числу поставлено в соответствие число . Тогда говорят, что на множестве определена функция , действующая в множество .

Обычно используют обозначения:

, , (1)

или

: . (2)

В этом пособии будем придерживаться, в основном, второго обозначения.

Множество называется областью определения функции, а множество – областью, или множеством значений. Величина называется независимой переменной, или аргументом, а называется значением функции. Часто как синоним слова функция используют термин «отображение», называют прообразом, а , где – его образом.

Можно отметить значительное разнообразие вариантов происхождения и задания функций. В одних случаях функции определяются теми или иными формулами. Например, =; здесь упомянутое правило , по которому прообразу ставится в соответствие образ имеет вид «возвести в квадрат». Или другой пример: есть значение меньшего корня уравнения . В различных технических устройствах используют всевозможные датчики, которые показывают, как те или иные физические величины – температура, скорость, сила тока и т.п. зависят от других.

Определение 4.2. Графиком функции называется множество вида

,

оно представляет собой множество упорядоченных пар чисел, которое обычно интерпретируют как множество точек плоскости в декартовой системе координат.

Изображение графика функции позволяет использовать зрительные возможности для получения представления о функции. Так, врач, рассматривая кардиограмму, способен сделать заключение о характере работы сердца. А кардиограмма – это график функции , где t – время, а y – электромагнитная интенсивность сердечной мышцы.

Над числовыми функциями можно производить различные арифметические операции.

Пусть даны две функции и , определенные на одном и том же множестве . Тогда функция , где - некоторое постоянное число, определяется как функция, в каждой точке принимающая значение ; функция – как функция, в каждой точке принимающая значение ; функция – как функция, в каждой точке принимающая значение ; в каждой точке равна , при условии .

Пусть функция :, а : . Тогда функция , определенная равенством , называется композицией функций и (сложной функцией).

4.2. Предел функции

Определение 4.3. Пусть функция определена на и - предельная точка множестваЧислоназывается пределом функции в точке , если для любогосуществует такое, что для всех , удовлетворяющих условию , выполняется неравенство.

Определение 4.3 обычно называют определением предела на языке “” или по Коши.

Предел функции в точке обозначают так:

.

С использованием логических символов определение можно переписать следующим образом:

()() ().

Определение предела функции в точке можно сформулировать в других терминах.

Определение 4.4. Пусть функция определена на множестве и - предельная точка множества . Число называется пределом функции в точке , если для любой последовательности,, из условий:

и ,

следует, что соответствующая последовательность значений функции сходится к числу , то есть.

Это определение обычно называют определение на языке последовательностей или по Гейне.

Теорема 4.1. Определения по Коши и по Гейне равносильны.

Доказательство. Пусть число является пределом функции в точке в смысле Коши. Выберем произвольную подходящую последовательность,, т. е. такую, для которойпри любоми. Покажем, чтоявляется пределом в смысле Гейне.

Зададим произвольное число и укажем для него такое, что для всехиз условияследует неравенство. В силу того, что, длянайдется такой номер, что для всехбудет выполняться неравенство. Это, в свою очередь, означает, что для всехбудет выполняться неравенство, т.е..

Докажем теперь обратное утверждение: предположим, что в смысле Гейне, и покажем, что числоявляется пределом функциив точкев смысле Коши. Предположим, что это неверно, т. е.

() () ()

и

().

В качестве рассмотрим, а соответствующие значениябудем обозначать. Тогда при любомвыполняются условияи. Отсюда следует, что последовательность,, является подходящей, но числоне является пределом функциив точке. Получили противоречие.Теорема доказана.

Замечание. Из определения предела функции по Гейне следует, что функция не может иметь в точке двух разных пределов.

Замечание. Понятие предела функции в точке есть локальное понятие: существование и значение предела полностью определяется значениями функции в как угодно малой окрестности этой точки.

Рассмотрим несколько примеров.

Пример 4.1. Пусть

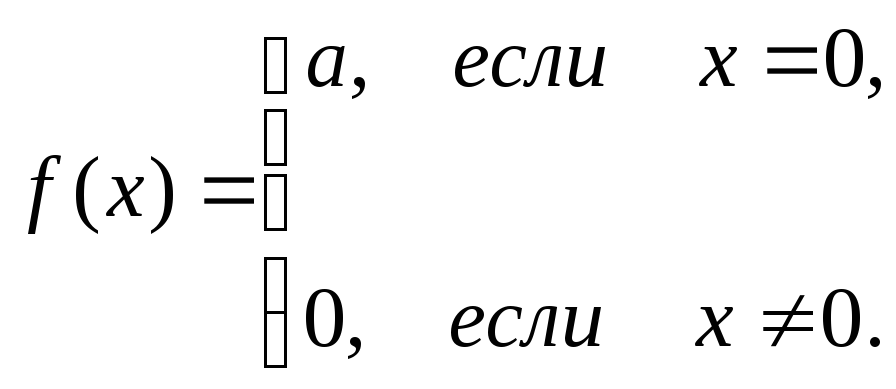
Если мы воспользуемся определением 4.4, то легко убедимся, что

.

Действительно, если ,, - произвольно выбранная бесконечно малая последовательность, для которойпри любом, тои, следовательно,. Как видим, значение предела не зависит отa.

Этот пример убедительно иллюстрирует факт, вытекающий из определений 4.3 и 4.4: существование предела функции в точкеи его значение никак не связаны с самим значением, в точкеможет вообще не иметь никакого значения.

Пример 4.2. Пусть . Тогда

.

Это легко вытекает из определения 4.4 и из свойств последовательностей: если , то.

Пример 4.3. Пусть - функция Дирихле:

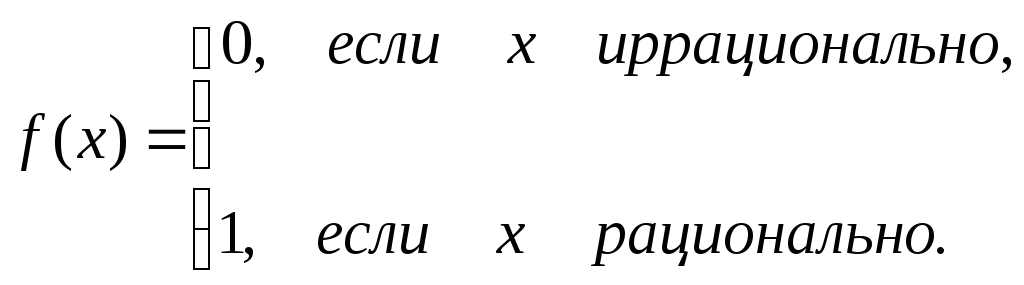
Покажем, что не существует, здесь- произвольно выбранное число.

Для доказательства рассмотрим две последовательности и, для которых

1) ,рационально при любоми;

2) ,иррационально при любоми(докажите, что такие последовательности существуют).

Тогда ии, так как 0 и 1 - разные числа, пределв точкене существует.

Задача 4.1.Приведите пример функции, заданной на множествевсех действительных чисел, которая имеет предел только в одной точке.