3.10. Бесконечно большие последовательности

В некоторой степени аналогом сходящихся последовательностей служат так называемые бесконечно большие последовательности.

Определение 3.10. Последовательность ,, называется бесконечно большой (иначе), если для любого положительного числасуществует такой номер, начиная с которого выполняется неравенство, т.е. ее члены по абсолютной величине становятся и остаются больше любого наперед заданного положительного числа.

Или, в формальной записи,

(() () ():.

Следует различать понятие «бесконечно большая последовательность» и «неограниченная последовательность». Именно, любая бесконечно большая последовательность является неограниченной последовательностью (докажите!), но неограниченная последовательность необязательно бесконечно большая.

Задача 3.18. Докажите, что =является неограниченной последовательностью, но не является бесконечно большой.

Рассмотрение бесконечно больших последовательностей расширяет понятие сходимости. Однако термин «сходящаяся последовательность» мы будем относить к понятию последовательности, имеющей конечный предел.

Частными случаями бесконечно больших последовательностей являются последовательности, для которых и. Формально они определяются так:

()() (): ,

()() ():.

Связь между бесконечно большими и бесконечно малыми последовательностями выражается следующей теоремой.

Теорема 3.18. Если последовательность ,, бесконечно большая, то- бесконечно малая последовательность.

Доказательство. Выберем произвольно число . Тогда для числанайдется такой номер, что для всехвыполнено неравенство. Тогда для этих же значенийn .

Справедливо и обратное утверждение: если последовательность - бесконечно малая последовательность, то- бесконечно большая (докажите!).

Дополнительное представление о свойствах бесконечно больших последовательностей помогут получить следующие утверждения, которые предлагается доказать самостоятельно.

Задача 3.19. Докажите, что последовательность является бесконечно большой, причем.

Задача 3.20. Если и, то. Докажите.

Задача 3.21. Если и, то. Докажите.

Задача 3.22. Если , а последовательность,, ограничена, то.

Задача 3.23. Докажите, что любая последовательность может быть представлена в виде суммы двух бесконечно больших последовательностей.

Задача 3.24. Докажите, что если последовательность не ограничена, то она содержит бесконечно большую подпоследовательность.

Задача 3.25. Докажите, что если последовательность ,, не ограничена и монотонно возрастает, то.

Задача 3.26. Докажите, что любая последовательность содержит монотонную подпоследовательность.

3.11. Еще раз о числовых множествах

Использование числовых последовательностей и понятия сходимости позволяют расширить представления о свойствах числовых множеств.

Рассмотрим несколько определений, характеризующих положение точки относительно множества.

Определение 3.11.Пусть- некоторое множество действительных чисел. Точканазывается предельной точкой этого множества, если для любогосуществует точка, для которой.

Теорема 3.19.Точкаявляется предельной точкой множествав том и только в том случае, когда существует последовательность,, обладающая следующими свойствами:

1. для любого ,

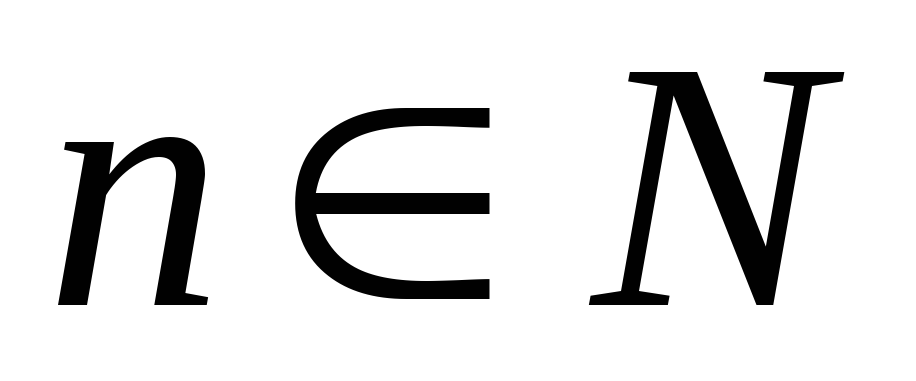
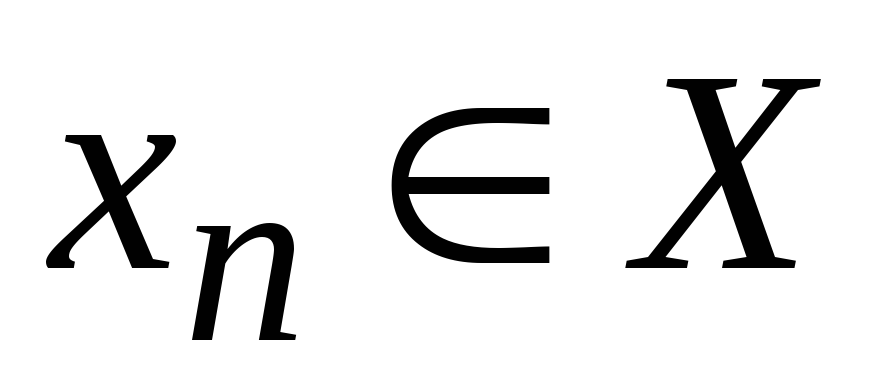2. при любом ,

3. .

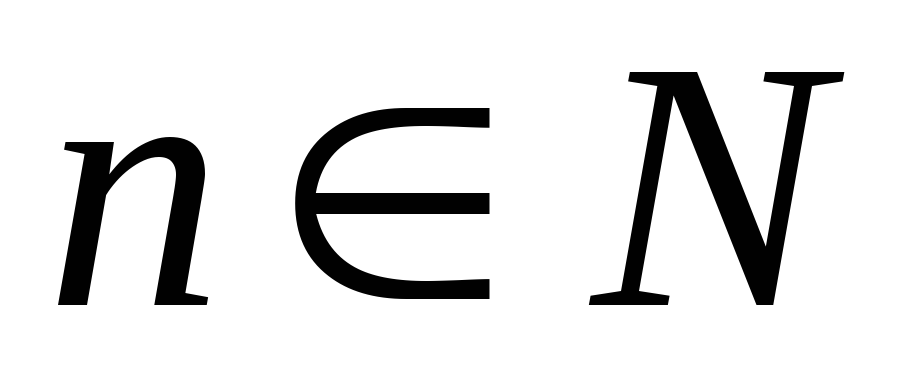
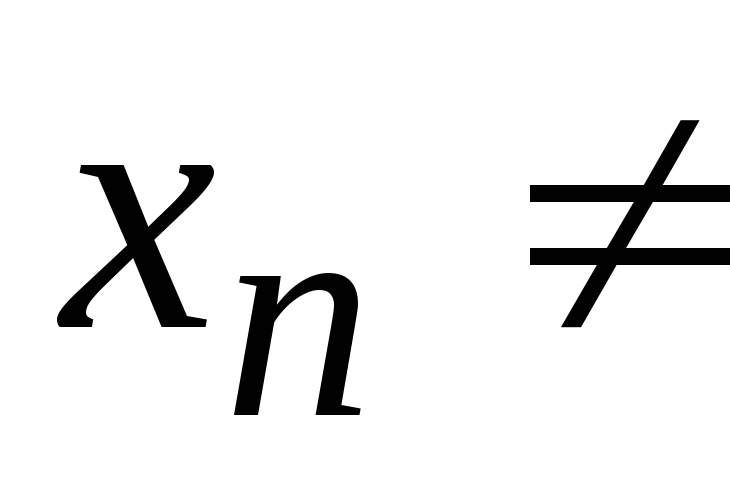
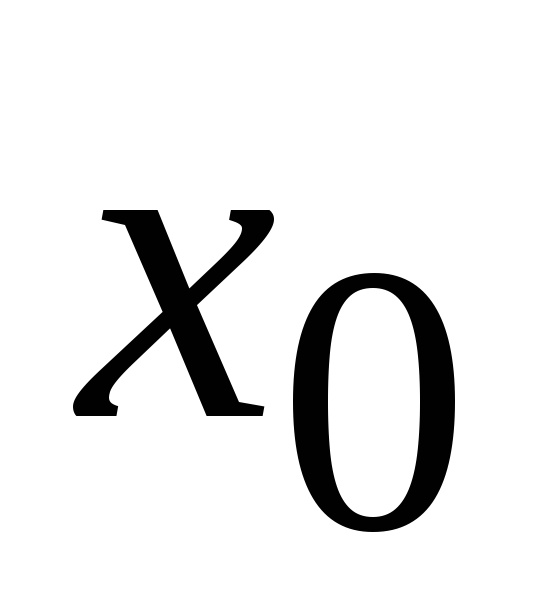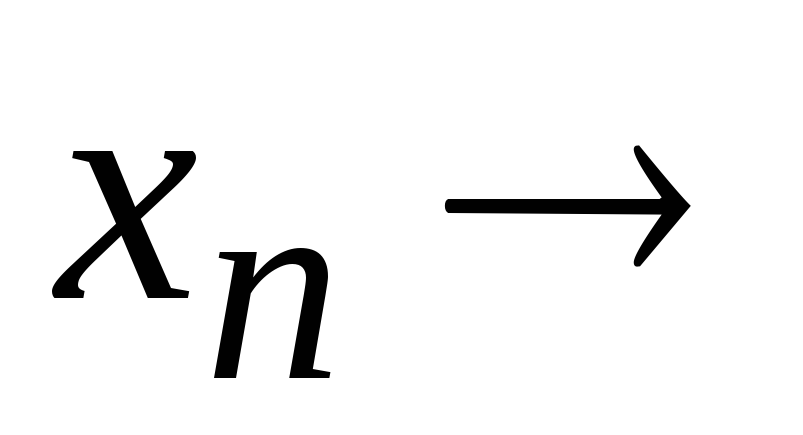
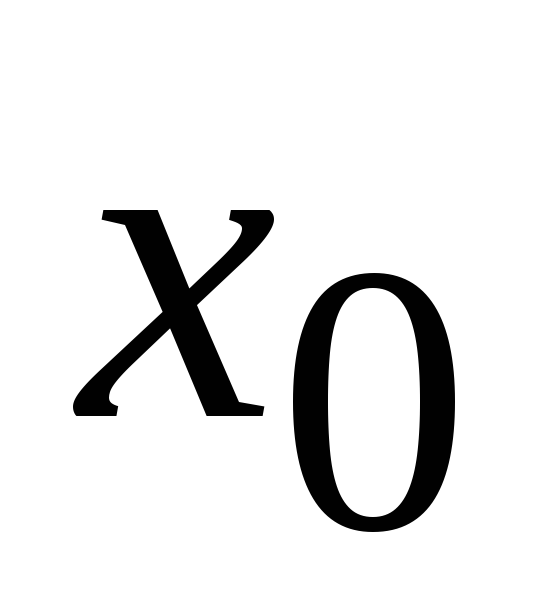В дальнейшем такую последовательность будем называть подходящей.

Доказательство.Пусть- предельная точка множества. Рассмотрим бесконечно малую последовательностьположительных чисел. Для каждогонайдется точка, для которой. Ясно, что обнаруженная таким образом последовательность,, является подходящей.

Обратно, если ,, - подходящая последовательность, то для любогосуществует такое, что для всехвыполнены неравенства. Полагая, убеждаемся, что, т.е. точка- предельная точка множества.Теорема доказана.

Множество всех предельных точек множества часто называют производным множеством и обозначают.

Задача 3.27.Для следующих множеств укажите множество всех предельных точек:

а) =;

б) =;

в) =, т.е. состоит из двух точек;

г) =;

д) - множество всех рациональных точек из отрезка;

Задача 3.28. Приведите пример множества, для которого.

Определение 3.12.Замыканиеммножестваназывается объединениеи:

=.

Определение 3.13. Множество называется замкнутым, если=.

Иначе, замкнутое множество – это множество, содержащее все свои предельные точки.

Задача 3.29.Докажите, что множества=и=- замкнутые множества, а множества=,=,- множество всех рациональных точек из отрезка- незамкнутые.

Задача 3.30.Докажите, что объединение двух замкнутых множеств есть множество замкнутое.

Задача 3.31.Приведите пример такой совокупности замкнутых множеств, объединение которых незамкнуто.

Определение 3.14. Пусть- некоторое множество действительных чисел. Точканазывается внутренней точкой множества, если существует такое число, что интервалсодержится в.

Множество всех внутренних точек множества называется его внутренностью и обозначается .

Ясно, что для любого множества.

Определение 3.15. Множество называется открытым, если выполняется равенство=. Иначе, открытое множество - это множество, все точки которого внутренние.

Задача 3.32.Докажите, что любой интервал – открытое множество.

Задача 3.33. Докажите, что любое открытое множество есть объединение попарно непересекающихся интервалов.

Задача 3.34. Докажите, что множествооткрыто тогда и только тогда, когда дополнение- замкнуто.

Задача 3.35. Докажите, что объединение любой совокупности открытых множеств открыто.

Задача 3.36.Приведите пример такой совокупности открытых множеств, пересечение которых не является открытым.

Доказательство многих утверждений математического анализа может быть основано на следующей важной лемме.

Лемма Гейне - Бореля. Пусть- замкнутое ограниченное множество, а,, некоторая совокупность открытых множеств. Пусть. Тогда найдется такое конечное подмножествомножества, для которого. Другими словами, всякое покрытие замкнутого ограниченного множества открытыми множествами содержит конечное подпокрытие.

Задача 3.37. Докажите частный случай леммы Гейне- Бореля, когда– отрезок, а,, - интервалы.

Задача 3.38. Докажите лемму Гейне- Бореля в общем виде.

Определение 3.16. Множествоназывается нигде не плотным, если для любого интервала, где, найдется непустой интервал, содержащийся в, и непересекающийся с множеством.

Определение 3.17. Множествоназывается первой по Бэру категории, если его можно представить в виде объединения, где каждое из множествнигде не плотно. Часто такое множество называют тощим. Остальные множества называются множествами второй категории.

Задача 3.39.. Докажите, что- не тощее множество.