3.6. Бесконечно малые последовательности

Последовательности, стремящиеся к нулю, обычно выделяют в отдельный класс последовательностей.

Определение 3.4. Последовательность ,, называется бесконечно малой, если().

Это определение может быть сформулировано следующим образом:

, , - бесконечно малая последовательность(), (), ():.

Теорема 3.7. Для того чтобы последовательность ,, сходилась кнеобходимо и достаточно, чтобы разностьбыла бесконечно малой.

Доказательство этого утверждения очевидно.

Отметим несколько свойств бесконечно малых последовательностей.

Теорема 3.8. Алгебраическая сумма двух бесконечно малых последовательностей является бесконечно малой последовательностью.

Доказательство. Пусть ,, - бесконечно малые последовательности. Покажем, что- бесконечно малая последовательность. Выберем произвольно число. По определению, найдется такой номер, что для всехбудут выполнено неравенство:

.

Аналогично, найдется такой номер , начиная с которого выполняется неравенство:

.

Обозначим: . Тогда при всех

,

что означает: .Теорема доказана.

Следствие. Алгебраическая сумма конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью. (Докажите индукцией).

Теорема 3.9. Произведение бесконечно малой последовательности на ограниченную последовательность является бесконечно малой последовательностью.

Доказательство. Пусть ,, - бесконечно малая последовательность, а,, - ограниченная последовательность. Покажем, что- бесконечно малая последовательность.

По определению ограниченной последовательности найдется такое число , что для всехвыполняется неравенство. Выберем произвольно число. По определению бесконечно малой последовательности найдется такой номер, что для всехвыполняется неравенство:. Поэтому для всехимеем,то есть- бесконечно малая последовательность. Теорема доказана.

Следствие. Произведение бесконечно малой последовательности на сходящуюся последовательность является бесконечно малой последовательностью.

Следствие. Произведение конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.

3.7. Сходимость и арифметические операции

Следующие теоремы позволяют существенно облегчить вычисление пределов.

Теорема 3.10. Пусть последовательности и,, сходятся к числамисоответственно, тогда их сумма (разность) - сходящаяся последовательность, причем().

Доказательство. Докажем теорему для суммы двух последовательностей. По теореме 3.7 =,=- бесконечно малые последовательности. Тогда

()

является бесконечно малой (теорема 3.8), из этого следует, что .Теорема доказана.

Теорема 3.11. Пусть последовательности и,, сходятся к числамисоответственно, тогда их произведение - сходящаяся последовательность, причем.

Доказательство. Исходя из равенств =,=, где- бесконечно малые последовательности, получим: . Выражение справа согласно теоремам о бесконечно малых определяет бесконечно малую последовательность.Теорема доказана.

Теорема 3.12. Если последовательности и, где,, сходятся к числамисоответственно, причемотлично от нуля, то их отношение также сходящаяся последовательность и

.

Доказательство. Согласно результату задачи 3.8 раздела 3.4 существует такой номер , что для всех номероввыполняется неравенство, поэтому для тех же номеров выполняется неравенство

<.

Далее,

=.

В силу свойств бесконечно малых последовательностей числитель дроби есть бесконечно малая. Из условия

= <

при следует, что- ограниченная последовательность. Итак, разностьесть бесконечно малая последовательность и.Теорема доказана.

Пример 3.16. Для любого ,. Пусть сначала . Обозначим через. Заметим, что. Выразимпо формуле бинома Ньютона:. Поскольку все слагаемые справа положительны, то. Следовательно,. Приполучим. Если, то положим. По доказанному. Отсюда .

Задача 3.13. Показать как результат примера 3.16 следует из результата примера 3.14.

Теоремы об арифметических операциях над пределами и теорема о монотонной и ограниченной последовательности позволяют обосновать алгоритм для нахождения приближенного извлечения квадратного корня.

Пример 3.17. Доказать, что если , то последовательность, определенная соотношением

, ,

имеет предел, и он равен .

Так как и, тодля всех. Из неравенства о среднем арифметическом и среднем геометрическом двух чисел следует, что

.

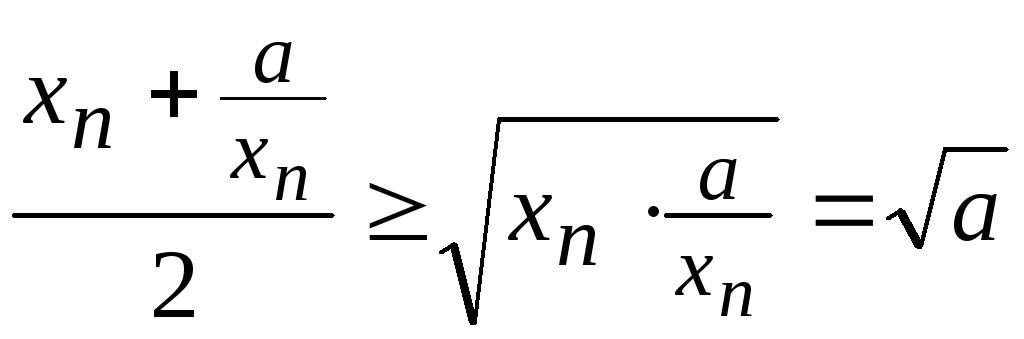Поэтому при каждом натуральном справедливо неравенствоили. Таким образом,

и последовательность является убывающей. Последовательность ограничена снизу, например, числом. По теореме Вейерштрасса она имеет предел, обозначим его через. Из неравенстваследует, что.

Перейдем к пределу в исходном соотношении

.

Учитывая, что (объясните, почему?), получим

,

то есть . Поскольку, то=.

Алгоритм вычисления в этом случае дает:

.