
int_kurs-podg_-ege_kasatkina-i_l_2012
.pdf
Физика для старшеклассников и абитуриентов
р4 = р2 + рп = 2ратм + рс + ратм = 3ратм + рс, |
(9) |
согласно (2) и (4).
Новый объем воздуха под нижним поршнем станет равен:
V3 = xS . |
(10) |
Подставим правые части равенств (8), (3), (9) и (10) в формулу (7):
3ратмhS = (3ратм + рс)хS, 3ратмh = (3pатм + рс)х. (11) Теперь нам предстоит решить систему уравнений (6) и (11)
относительно искомого расстояния х, исключив из них неизвестные давления. Давайте в этих уравнениях сначала раскроем скобки и сделаем приведение подобных членов, — может, мы их при этом немного упростим. Начнем с уравнения (6):
2ратмh = 2pатмh + pch – 2pатмх – рсх, 2ратмх = рс(h – x). (12)
Теперь проделаем то же самое с уравнением (11):
3ратмh = 3pатмх + рсх, 3ратм(h – x) = рсх. |
(13) |
Если теперь разделить левые и правые части уравнений (12)
и(13) друг на друга, то все неизвестные давления сократятся
имы сумеем найти расстояние х:
|
|
2ðàòìõ |
= |
|
pc (h−x) |
, |
|
2x |
|
= |
h−x , |
|||
|
|
|
3(h−x) |
|||||||||||
|
3ðàòì (h−x) |
|
|
pcx |
|
|
|
x |
||||||
2x2 = 3(h−x)2 , |
|
откуда |
õ 2 = (h−x) 3 . |
|||||||||||
Отсюда |
x = |
|
h 3 |
|
|
≈ 0,55 h . |
|
|
||||||
2+ |
3 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: х | 0,55h.
С7. Агрегат мощностью 50 кВт охлаждается проточной водой, текущей со скоростью 4 м/с по охватывающей агрегат трубке радиусом 5 мм. Начальная температура воды 10 0С. До какой температуры нагревается вода, если половина тепловой мощности агрегата идет на ее нагревание? Удельная теплоемкость воды 4200 Дж/(кг · К).
Обозначим N мощность агрегата, v — скорость течения воды, R — радиус трубки, t1 — начальную температуру воды, K — КПД нагревателя, c — удельную теплоемкость воды, U— плотность воды, t2 — температуру, до которой нагревается
290

Раздел II. Молекулярная физика и термодинамика
вода, Qпол — количество теплоты, пошедшее на нагревание воды, Qзатр — количество теплоты, затраченное агрегатом, m — массу воды, V — ее объем, l — длину водяного столбика, S — площадь сечения трубки, t — время нагревания.
Дано: |
Решение |
|
|
|
N = 50 кВт |
Мы записали в условии КПД рав- |
|||
v = 4 м/с |
ным 50%, потому что только полови- |
|||
R = 5 мм |
на, т.е. 50% выделяемого агрегатом |
|||
t1 = 10 0C |
тепла, идет на нагревание воды. |
|
||
K = 50% |
Запишем формулу КПД этого агре- |
|||
c = 4200 Дж/(кг · К) |
гата следующим образом: |
|
||
U = 1000 кг/м3 |
|
Q |
|
|
|
η = |
ïîë |
100% . |
(1) |
|
|
|||
|
|
Q |
|
|
|
|
|
||
|
|
çàòð |
|
|
Здесь Qпол — количество теплоты, пошедшее на нагревание воды:
Qпол = cm (t2 – t1). |
(2) |
Чтобы ввести в эту формулу известную нам скорость воды, выразим массу протекающей по трубке воды через ее плотность U и объем V, а объем, в свою очередь, — через некоторую длину столбика воды l = vt, где t — время, за которое некоторое сечение этого столбика воды пробегает длину l:
m = UV, где V = lS = vtS.
Здесь S = SR2 — площадь поперечного сечения трубки с водой. Собрав все эти равенства в формулу массы воды, получим:
m = UvtSR2. |
(3) |
Подставим правую часть равенства (3) вместо массы в формулу (2):
Q |
= UvtSR2 (t |
2 |
– t |
). |
(4) |
пол |
|
1 |
|
|
Теперь выразим затраченное агрегатом количество теплоты через его тепловую мощность:
Qзатр = Nt. |
(5) |
Нам осталось подставить правые части выражений (4) и (5) в формулу (1) и, сократив неизвестное время t, найти искомую температуру t1. Проделаем эти действия:
291
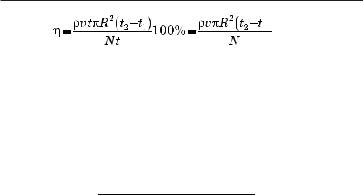
Физика для старшеклассников и абитуриентов





 .
.
Отсюда найдем t2:
t2 = t1 + |
ηN |
|
. |
|
πρvR2100% |
||||
|
||||
Задача в общем виде решена. Выразим величины мощности и радиуса в единицах СИ:
5 кВт = 5 · 103 Вт, 5 см = 5 · 10—2 м. Произведем вычисления:
t2 = 10 |
0Ñ + |
50 5 103 |
0С = 89,6 0С. |
3,14 1000 4 (5 10−2 )2 100 |
Ответ: t2 = 89,6 0С.
С8. Тепловой двигатель совершает круговой цикл, соответствующий графику на рис. 170. Цикл состоит из двух изохор 1–2 и 3–4, и двух адиабат 2–3 и 4–1. Найти КПД этого цикла.
Обозначим р1 давление газа в состоянии 1, р2 — давление газа в состоянии 2, V1 — объем газа в состоянии 1, V2 — объем газа в состоянии 2, K — КПД процесса, Q1 — количество теплоты, полученное газом в изохорном процессе 1–2, Q2 — количество теплоты, отданное газом в изохорном процессе 3–4, Q — количество молей газа, R — молярную газовую постоянную, 'Т1 — изменение температуры газа в процессе 1–2, 'Т2 — изменение температуры газа в процессе 3–4, р3 — давление газа в состоянии 3, р4 — давление газа в состоянии 4.
Дано: |
|
Решение |
|
||
р1 = 10 кПа |
|
В изохорном процессе 1–2 газ получает |
р2 = 50 кПа |
|
извне количество теплоты Q1. Больше ни в |
V1 = 2 л |
|
одном процессе этого графика он теплоты не |
V2 = 6 л |
|
получает. |
|
|
Ведь в адиабатных процессах 2–3 и 4–1 |
K — ? |
|
|
|
передачи тепла не происходит, а при изохор- |
|
|
ном уменьшении давления в процессе 3–4 газ охлаждается, т.е. он отдает тепло внешней среде в количестве Q2. Поэтому КПД этого кругового процесса равен:
η = Q1 −Q2 100%. |
(1) |
Q1 |
|
292

Раздел II. Молекулярная физика и термодинамика
Количество теплоты, полученное газом при изохорном увеличении давления, соответствующем участку 1–2 графика, в соответствии с первым законом термодинамики, когда работа расширения А = 0, равно изменению внутренней энергии газа:
Q1 = 32 νR T1 ,
где в соответствии с уравнением Менделеева—Клапейрона
(ð2 − ð1)V1 = νR T1.
С учетом этого
Q1 = 32(p2 − p1)V1. |
(2) |
При изохорном уменьшении давления, соответствующем участку 3–4 графика, количество теплоты Q2, выделенное в процессе охлаждения газа, найдем по аналогичной формуле:
Q2 = |
3 |
νR T2 |
= |
3 |
(p3 |
− p4 )V2 . |
(3) |
2 |
2 |
Нам осталось подставить правые части равенств (2) и (3) в формулу (1), и задача в общем виде будет решена. Проделаем эти действия:




 .
.
Здесь можно не переводить единицы величин в СИ, ведь все они сокращаются. Произведем вычисления:
(15−5)6
η= 1− ( ) 100%= 25%.50−10 2
Ответ: K = 25%.
С9. В калориметр налита вода массой 0,4 кг при 10 0С. В воду положили 0,6 кг льда при –40 0С. Определить температуру после установления теплового равновесия. Удельная теплоемкость воды 4200 Дж/(кг . К), удельная теплоемкость льда 2100 Дж/(кг . К), удельная теплота плавления льда 3,3 . 105 Дж/кг.
293

Физика для старшеклассников и абитуриентов
Обозначим m1 массу воды в калориметре, t1 — ее начальную температуру, m2 — массу льда, t2 — начальную температуру льда, t — температуру, установившуюся в калориметре после всех тепловых процессов, c1 — удельную теплоемкость воды, c2 — удельную теплоемкость льда, O — удельную теплоту плавления льда, tо = 0 0С — температуру плавления льда и кристаллизации воды, t — температуру, установившуюся
вкалориметре, Q1 — количество теплоты, отданное водой
вкалориметре при охлаждении от температуры t1 до tо, Q2 — количество теплоты, необходимое льду, чтобы нагреться от температуры t2 до tо , Q3 — количество теплоты, которое выделит вода, если, остыв до 0 0С, полностью превратится
влед, Q4 — количество теплоты, необходимое льду, чтобы полностью растаять.
Дано: |
|
Решение |
|
||
m1= 0,4 кг |
|
Глядя на массы воды и льда, |
t1 = 10 оС |
|
а также на их начальные тем- |
m2 = 0,6 кг |
|
пературы, сразу и не скажешь, |
t2 = –40 оС |
|
что произошло: то ли весь лед |
tо = 0 оС |
|
растаял, то ли вся вода замерз- |
c1 = 4200 Дж/(кг . К) |
|
ла. Ведь масса льда и его началь- |
c2 = 2100 Дж/(кг . К) |
|
ная отрицательная температу- |
O = 3,3 . 105 Дж/кг |
|
ра достаточно велики по срав- |
|
|
нению с массой воды в калори- |
t — ? |
|
метре и ее начальной темпера- |
|
|
турой. Чтобы понять, в каком |
агрегатном состоянии окажутся эти вещества, давайте подсчитаем, сколько теплоты Q1 выделит вода массой m1 при охлаждении от t1 = 10 0С до tо = 0 0С, сколько теплоты Q2 потребуется льду, чтобы нагреться от температуры t2 = – 40 0С до tо = 0 0С, и сколько теплоты нужно этому льду, чтобы полностью растаять, — а потом сравним полученные величины.
Вода при охлаждении от 10 0С до 0 0С выделит
Q1 = c1m1(to – t1) = 4200 · 0,4(0 – 10) Дж = –16 800 Дж теплоты.
Льду, чтобы нагреться до 0 0С, требуется
Q2 = c2m2(to – t2) = 2100 · 0,6(0 – (–40)) Дж = = 50 400 Дж теплоты.
294

Раздел II. Молекулярная физика и термодинамика
Значит, теплоты, выделенной водой при охлаждении до 0 0С, недостаточно, чтобы лед нагрелся до температуры плавления, т.е. тоже до 0 0С. Вода остынет до 0 0С и станет кристаллизоваться, т.е. превращаться в лед. Если она полностью превратится в лед, то выделит еще
Q3 = Om1 = 3,3 . 105 . 0,4 Дж = 132 000 Дж теплоты.
Теплоты Q1 + Q3 = (16 800 + 132 000) Дж = 148 800 Дж хватит льду, чтобы нагреться до температуры таяния, т.е. до 0 0С. Но хватит ли ее, чтобы его полностью растопить? Чтобы весь лед растаял при 0 0С, ему надо еще
Q4 = Om2 = 3,3 . 105 . 0,6 Дж = 198 000 Дж теплоты.
Значит, чтобы весь лед нагреть до 0 0С и полностью растопить, ему надо сообщить Q2 + Q4 = 50 400 + 198 000 Дж = 248 400 Дж теплоты.
Следовательно, теплоты, выделенной водой при охлаждении и замерзании, хватит на то, чтобы лед нагрелся до 0 0С, но не хватит на то, чтобы он весь растаял. Значит, окончательная температура будет 0 0С.
Ответ: t = 0 0С.
С10. В калориметр налита вода массой 0,25 кг при температуре 25 0С. В эту воду впустили стоградусный пар массой 10 г. Теплоемкость калориметра 1000 Дж/К, Удельная теплоемкость воды 4200 Дж/(кг . К), удельная теплота парообразования 2,3 . 106 Дж/К. Найти температуру при тепловом равновесии этих тел.
Обозначим m1 массу воды в калориметре, t1 — начальную температуру этой воды, m2 — массу водяного пара, t2 — начальную температуру пара, C — теплоемкость калориметра, t — установившуюся в калориметре температуру после всех тепловых процессов, c — удельную теплоемкость воды, r — удельную теплоту парообразования, Q1 — количество теплоты, полученное холодной водой при нагревании от температуры t1 до t, Q2 — количество теплоты, полученное холодным калориметром при нагревании тоже от температуры t1 до t, Q3 — количество теплоты, отданное паром при конденсации, в процессе которой его температура не менялась, Q4 — количество теплоты, отданное водой, образовавшейся из горячего пара при охлаждении от температуры t2 до t.
295

Физика для старшеклассников и абитуриентов
Дано: |
|
Решение |
|
||
m1 = 0,25 кг |
|
Согласно закону сохранения тепло- |
t1 = 25 оС |
|
вой энергии сумма количеств теплоты, |
m2 = 10 г |
|
полученных и отданных в этих про- |
t2 = 100 оС |
|
цессах, равна нулю: |
C = 1000 Дж/К |
|
Q1 + Q2 + Q3 = 0. |
c = 4200 Дж/(кг . К) |
|
|
|
Здесь |
|
r = 2,3 . 106 Дж/К |
|
|
|
Q1 = cm1(t – t1), Q2 = C(t – t1), |
|
|
|
|
|
|
|
t — ? |
|
Q3 = –rm2, Q4 = cm2(t – t2). |
|
Сложим правые части этих выражений и приравняем их нулю, откуда найдем искомую температуру t:
cm1(t – t1) + C(t – t1) – rm2 + cm2(t – t2) = 0.
Мы записали уравнение теплового баланса. Раскроем скобки, члены, содержащие искомую температуру t, оставим по одну сторону от знака равенства, а не содержащие — перенесем в другую, вынесем t за скобки и определим:
cm1t – cm1t1 + Ct – Ct1 – rm2 + cm2t – cm2t2 = 0,
сm1t + Ct + cm2t = cm1t1 + Ct1 + rm2 ,
t(c(m1 + m2) + C) = t1(cm1 + C) + rm2 ,
t = t1(cm1 + C) + rm2 c(m1 + m2 ) + C
Выразим в единицах СИ массу пара: 10 г = 0,01 кг. Произведем вычисления:
t = |
25(4200 0,25 |
+ 1000) |
+ 2,3 |
106 |
4200(0,25 |
|
|
0С | 37 0С. |
|
|
+ 0,01) + 1000 |
|||
Ответ: t | 37 0С.
С11. 10 молей идеального газа нагрели на 100 К. В процессе нагревания давление газа росло прямо пропорционально его объему. Какое количество теплоты было сообщено газу?
Обозначим Q количество молей, 'Т — изменение температуры газа, р — давление, k — коэффициент пропорциональности между давлением и объемом V, Q — количество теплоты, полученное газом, 'U — изменение его внутренней энергии,
296
Раздел II. Молекулярная физика и термодинамика |
|
|||
А — работу против внешних сил, R — молярную газовую посто- |
||||
янную, p1 V1 и T1 — давление, объем и температуру в начальном |
||||
состоянии газа, p2 V2 и T2 — давление, объем и температуру в |
||||
конечном состоянии газа. |
|
|
|
|
Дано: |
Решение |
|
|
|
Q = 10 моль |
Согласно первому закону термодинамики |
|||
'Т = 100 К |
количество теплоты Q, полученное газом, |
|||
р = kV |
равно сумме изменения его внутренней энер- |
|||
|
гии 'U и работы против внешних сил A: |
|
||
Q — ? |
Q = 'U + A. |
|
|
(1) |
Изменение внутренней энергии найдем, воспользовавшись |
||||
соответствующей формулой: |
|
|
|
|
|
'U = 3QR'T = 1,5 QR'T. |
|
(2) |
|
|
2 |
|
|
|
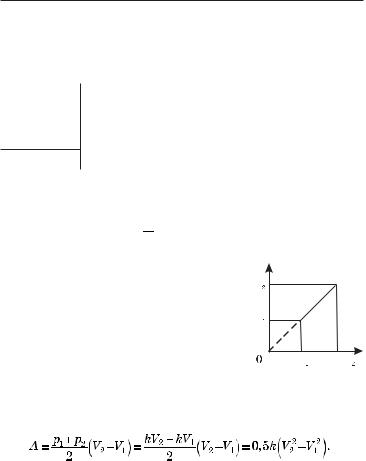
Работу расширения газа здесь найти |
p |
|
|
|
труднее, поскольку процесс не является |
p |
|
c |
|
изобарным, а другой формулы для на- |
|
|
|
|
хождения работы расширения газа мы не |
p |
b |
|
|
знаем. Тогда воспользуемся графическим |
|
|
||
способом. Изобразим на графике в коорди- |
|
a |
d |
|
натах р–V процесс, при котором давление |
|
|||
|
V |
V |
||
газа прямо пропорционально его объему |
|
|||
|
Рис. 182 |
|||
(рис. 182). На таком графике работа А |
|
|||
|
|
|
||
равна площади трапеции abcd, а площадь трапеции равна про- |
||||
изведению полусуммы ее оснований и высоты. Следовательно, |
||||
(3)
Теперь запишем уравнение Менделеева — Клапейрона для начального и конечного состояний газа:
p1V1 = QRT1 |
и р2V2 = QRT2. |
|||
Согласно условию |
p1 = kV1 |
и p2 = k V2. |
||
Подставим правые части этих равенств в два предыдущих |
||||
уравнения: |
|
|
|
|
kV2 = νRT |
и |
kV2 |
= νRT . |
|
1 |
1 |
|
2 |
2 |
А теперь вычтем из последнего уравнения предпоследнее. Так мы придем к правой части равенства (3):
297

Физика для старшеклассников и абитуриентов
kV22 − kV12 = νRT2 − νRT1 ,
k(V22 −V12 )= νR(T2 −T1)= νR T .
Тогда с учетом равенства (3)
А = 0,5QR'T. |
(4) |
Подставив равенства (2) и (4) в формулу (1), мы решим задачу в общем виде:
Q = 1,5QR'T + 0,5QR'T = 2QR'T.
Произведем вычисления:
Q = 2 · 10 · 8,31 · 100 Дж = 16620 Дж = 16,62 кДж.
Ответ: Q = 16,62 кДж.
С12. В идеальном газе происходит процесс, изображенный на рис. 171. Какое количество теплоты подведено к газу в этом процессе, начиная от состояния 1 и кончая состоянием 4?
Обозначим p1 давление газа в состояниях 1 и 2, V1 — объем газа в состоянии 1, р2 — давление газа в состояниях 3 и 4, V2 — объем газа в состояниях 2 и 3, V3 —объем газа в состоянии 4, Q — количество теплоты подведено к газу, начиная от состояния 1 и кончая состоянием 4, Q1 — количество теплоты, полученное газом при изобарном расширении (участок 1–2), Q2 — количество теплоты, полученное газом при изохорном нагревании (участок 2–3), Q3 — количество теплоты, полученное газом при изобарном расширении (участок 3–6), 'U1 — изменения внутренней энергии газа в процессе 1–2, А1 — работа расширения газа в процессе 1–2, Q — количество молей газа, R — молярную газовую постоянную, 'T1 — изменение температуры газа в процессе 1–2, А2 — работа газа в процессе 2–3, 'T2 — изменение температуры газа в процессе 2–3.
Дано:
p1= 100 кПа p2 = 200 кПа V1 = 2 л
V2 = 6 л
V3 = 8 л
Q — ?
Решение
Количество теплоты, полученное газом в этом процессе, равно сумме количеств теплоты, полученных на каждом из трех его участков:
Q = Q1 + Q2 + Q3 . |
(1) |
Согласно первому закону термодинамики количество теплоты Q1, полученное
298

Раздел II. Молекулярная физика и термодинамика
газом при изобарном расширении (участок 1–2), равно сумме изменения внутренней энергии газа 'U1 и работе А1, совершенной газом против внешних сил:
|
|
|
Q1 = 'U1 + A1, |
|
где, |
|
|
|
|
'U1 = |
3 νR T |
, А1 = р1(V2 – V1) и р1(V2 – V1) = QR'T1, |
|
|
|
2 |
1 |
|
|
|
|
|
|
|
поэтому мы вправе записать: |
|
|||
|
Q1 = 32 p1(V2 −V1)+ p1 (V2 −V1)= 2,5p1 (V2 −V1). |
(2) |
||
Количество теплоты Q2, полученное газом при изохорном нагревании (участок 2–3), равно только изменению внутренней энергии газа 'U2, ведь при изохорном процессе работа газа
А2 = 0.
Поэтому, в соответствии с предыдущими рассуждении, мы запишем:
Q2 = |
3 |
νR T2 |
= 1,5(p2 − p1)V2 , |
(3) |
2 |
ведь теперь, согласно уравнению Менделеева — Клапейрона,
(р2 – р1)V2 = QR'T2.
Процесс, соответствующий участку 3–4, снова является изобарным, поэтому по аналогии с предыдущим изобарным процессом мы запишем:
Q3 = 2,5p2 (V3 −V2 ). |
(4) |
Подставив правые части выражений (2), (3) и (4) в равенство (1), мы решим задачу в общем виде:
Q = 2,5p1(V2 −V1)+ 1,5(p2 − p1)V2 + 2,5p 2 (V3 −V2 ).
Задача в общем виде решена. Но правую часть этого выражения можно упростить: раскрыть скобки и сделать приведение подобных членов. Проделаем эти действия и мы:
Q = 2,5p1V2 − 2,5p1V1 + 1,5p2V2 − 1,5p1V2 + 2,5p2V3 − 2,5p2V2 = = p1V2 − 2,5p1V1 − p2V2 + 2,5p2V3 = p1 (V2 −2,5V1)+ p2 (2,5V3 −V2 )
299
