Конечные множества

Большинство задач комбинаторики можно сформулировать как задачи теории конечных множеств. Поэтому целесообразно напомнить некоторые положения «теории конечных множеств».

Всякая совокупность объектов произвольного рода образует множество. При этом сами объекты называют элементами данного множества. Множества обозначают большими латинскими буквами, их элементы – малыми латинскими буквами.

Запись обозначает, что a есть элемент A, или а принадлежит А, а запись – a не является элементом множества A, или а не принадлежит множеству А.

Множество считают определённым, если о любом объекте можно сказать, является он элементом данного множества или нет.

По количеству элементов множества делят на пустые, конечные и бесконечные.

Пустым называют множество, не содержащее ни одного элемента. Обозначают такое множество символом .

Если каждый элемент множества В принадлежит множеству А, то В называют подмножеством множества А.

Обозначают: или.

Читают: множество В входит в множество А или множество содержит множествоВ.

Теорема 1. Если и , то .

 Доказательство проведем методом «от противного». Пусть множества ине совпадают. Тогда без ограничения общности можно считать, что существует элементиз множества, который не принадлежит множествуВ. Следовательно, множество не может быть подмножеством множества. Однако по условию множество А является подмножеством множества В. Получили противоречие. Полученное противоречие доказывает справедливость равенства. Значит, множества иравны.

Теорема доказана.

На основе теоремы 1основан метод доказательства равенства множеств, который называют«методом включения».

Непустое подмножество множестваназываютсобственным подмножеством, если .

Несобственными подмножествами множества являются пустое множество и само множество.

Бесконечным называют множество равномощное некоторому собственному подмножеству.

Конечным называют множество, которое не равномощно ни какому собственному подмножеству.

Количество элементов множества обозначаютn(A).

Операции над множествами

Суммой или объединением множеств иназывают множествоС, содержащее все те и только те элементы, которые принадлежат либо множеству А, либо множеству .

Обозначают: C=A B.

Если A, A…A – некоторые множества, то A A … A является множеством, состоящим из всех тех и только тех элементов, которые входят хотя бы в одно из множеств A, A … A.

Операцию нахождения объединения называют сложением множеств.

Сложение множеств обладает свойствами коммутативности и ассоциативности. То есть, для произвольных множеств ,исправедливы равенства:

A B = B A,

A (BC) = (AB)C.

Первое из этих равенств вытекает из определения суммы. Второе есть следствие того, что A (B C) и (A B) C есть совокупность элементов, входящих хотя бы в одно из множеств , либо, либо.

Множество , которому принадлежат те и только те элементы, которые являются как элементами множества, так и элементами множества, называютпересечением множеств и.

Обозначают: C=A B.

Если A, A…A – некоторые множества, то A A … A является множеством, состоящим из всех тех и только тех элементов, которые входят в каждое из множеств A, A … A (являются общими для этих множеств).

Операцию нахождения пересечения называют пересечением множеств.

Пересечение множеств коммутативно и ассоциативно. То есть, для произвольных множеств ,исправедливы равенства:

A B = BA,

A (BC) = (AB)C.

Напомним, что операции объединения и пересечения множеств обладают также свойством дистрибутивности. То есть, для произвольных множеств ,ивыполняются равенства:

A (B C) = (А В) (А С),

A ( В С) =( A В) (А С).

Наглядно операции над множествами можно иллюстрировать, изображая множества в виде кругов (их называют «кругами Эйлера» или «диаграммами Эйлера-Венна») или других фигур на плоскости.

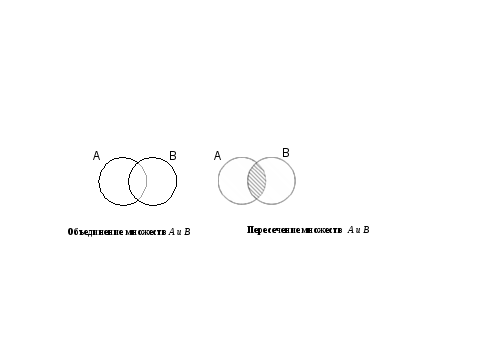Рис.3

Разностью множеств иназывают множество, содержащее те и только те элементы, которые принадлежат множествуи не принадлежат множеству.

Обозначают \.

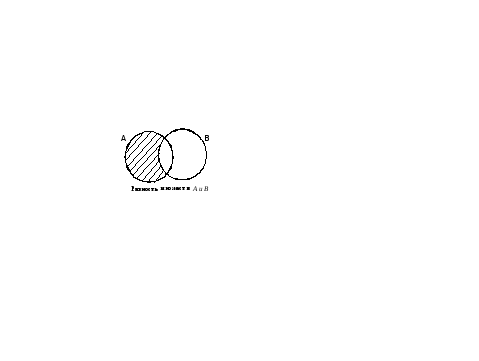Рис.4

Операцию нахождения разности множеств называют вычитанием множеств. Вычитание множеств не коммутативно и не ассоциативно, то есть, существуют множества ,итакие, что

\ В \ и \ (\С)(\) \С.

Сформулируем и докажем некоторые утверждения теории множеств, необходимые для изложения дальнейшего материала.

Лемма 1. Для любых множеств А и В справедливо равенство:

B=(A B) (B \ ). (1)

 Докажем данное утверждение методом включения, то есть покажем что B(A B) (B \ A) и (A B) (B \ A)В. Пусть – произвольный элемент множества(A B) (B \ A). Тогда, по определению объединения, либо x (A B), либо x (B \ A). Далее, по определению пересечения и разности, получим, что и , или и . Отсюда, по дистрибутивному закону конъюнкции относительно дизъюнкции, получаем, что и . Поскольку по законам логики высказываний выражение в скобках является тождественно истинным высказыванием, то элемент принадлежит множествуи первое включение доказано. Используя обратную цепочку рассуждений легко показать, что второе включение также имеет место.

Таким образом, лемма 1 доказана.

Лемма 2. Для произвольных множеств А и В справедливо равенство: (A B) (B \ A)=. (2)

 Доказательство проведем методом «от противного». Предположим, что равенство (2) не выполняется.

Тогда, существует хотя бы один элемент, который принадлежит множеству (A B)(B \ А)

Пусть x(A B) (B \ А), тогда по определению пересечения x(AB) и \А. Далее, применяя определения пересечения и разности получим, что () и . Отсюда и . Поскольку выражение в скобках является тождественно ложным, то предположение неверно. Полученное противоречие доказывает справедливость равенства (2).

Лемма 2 доказана.

Теорема 2. Число элементов в объединении двух непересекающихся множеств равно сумме чисел элементов в каждом из них, то есть, если п(A)=a, n (B)=b и A B=, то n (A B)=a+b.

Замечание. Данное утверждение справедливо для любого конечного числа попарно непересекающихся конечных множеств.

n(A)=a(i=), AA=, ij (i,j=) n( A) =a.

Лемма 3. Для любых множеств А и В справедливо равенство:

n (B \ A) = n (B) – n (A B). (3)

 Согласно лемме 1 B=(AB)(B \ A). Следовательно, n(B)=n((A B)(B \ A)). По лемме 2 (A B)(B \ A)=. Следовательно, по теореме 1, имеем n(B)=n(A B)+n(B \ A).

Отсюда, n(B \ A)=n(B)–n(A B). Лемма 3 доказана.

Теорема 3. Число элементов в объединении двух произвольных конечных множеств равно сумме чисел элементов в каждом из них, уменьшенной на число элементов в пересечении данных множеств, то есть n (A B) = n (A) + n (B) – n (A B).

 Докажем сначала, что для произвольных множеств A и B выполняется равенство A B=A (B \ A) (*).

Пусть x произвольный элемент множества A (B \ A). Тогда, по определению объединения, xA или x(B \ A). Применяя определение разности множеств, получим x A (xB xA). Отсюда, по дистрибутивности дизъюнкции относительно конъюнкции, имеем ( xA xB ) ( xA xA ). Так как последнее выражение в скобках является тождественно истинным, то xAxB. Откуда по определению объединения получаем xA B. Таким образом, A (B \ A)A B.

Аналогично доказывается включение A B A (B \ A) и по теореме 1 равенство (*) доказано.

Докажем теперь, что для любых множеств A и B выполняется равенство A (B \ A) =  (**). Доказательство проведем методом «от противного».

Предположим, что существуют множества A и B такие, что A(B \ A) ≠ . Тогда найдется хотя бы один элемент x принадлежащий множеству A (B \ A). По определению пересечения множеств x A и x (B \ A). Далее, по определению разности множеств, x A (x B x A). Отсюда x A x A x B. Так как высказывание x A x A является тождественно ложным, то мы получили противоречие, которое доказывает справедливость равенства (**).

Таким образом, учитывая равенства (*), (**) и теорему 2, получаем

n(A B)=n(A(B \ A))=n(A)+n(B \ A)=n(A)+n(B)–n(BA).

Теорема. 3 доказана.

Рассмотрим задачу, при решении которой используются приведенные теоретические положения.

Задача 1. В классе «Грифендор» учатся 40 студентов. У них есть возможность посещать предметы по выбору. 23 студента занимаются наукой прорицания, 11 занимаются предметом защиты от темных сил и 8 студентов, используя часы для возвращения в прошлое, занимаются и наукой прорицания, и предметом защиты от темных сил. Есть ли в группе студенты, которые не занимаются ни наукой прорицания, ни предметом защиты от темных сил?

Решение. Анализ условия показывает, что в задаче речь идёт о множестве А – студентов группы (n(A)=40), множестве В – студентов, которые занимаются наукой прорицания (n(B)=23), множестве С – студентов, посещающих уроки по защите от темных сил (n(C)=11).

И

3

1

з условия также следует, чтоB A, C A и B C , причём n(B C) = 8. И

2

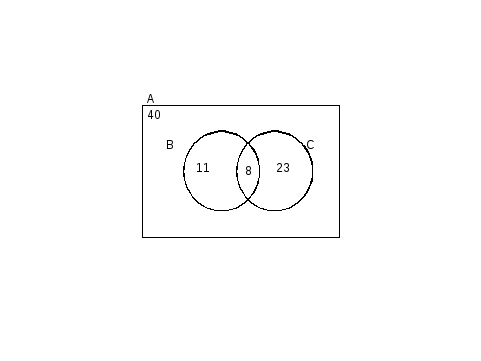зобразим описанную ситуацию с помощью кругов Эйлера (Рис.5).

Рис.5

Чтобы найти число студентов, которые не занимаются ни наукой прорицания, ни предметом защиты от темных сил необходимо из числа всех студентов группы вычесть число студентов, занимающихся или наукой прорицания, или предметом защиты от темных сил, то есть число n(B C).

п(B C)= n(B) + n(C) – n(B C) = 26 (студентов)

Так как всего в группе 40 студентов, то не занимаются ни наукой прорицания, ни предметом защиты от темных сил: 40–6=14 (студентов).

Ответ: 14 студентов, которые не занимаются ни наукой прорицания, ни предметом защиты от темных сил.

Теорема 3.1. Справедлива следующая формула для нахождения числа элементов в объединении трех произвольных конечных множеств:

n(ABС)=n(A)+n(B)+n(С)–n(AB)–n(AС)–n(ВС)+n(ABС).

 Данное утверждение является следствием теоремы 3.

В самом деле, так как сложение множеств обладает свойством ассоциативности, то A B С = (A B) С. Тогда, по теореме 3

n (A BС) = n(A B) +n(С) – n((A B)С). (*)

Применяя далее свойства дистрибутивности пересечения множеств относительно сложения, ассоциативности и идемпотентности пересечения множеств, а также теорему 3, получим:

n((A B) С) = n(( A С) (B С)) = n(A С)+n(В С)–

−n((A С)(B С)) = n(A С)+n(В С)–n(A B С). (**)

и n(A B) = n(A) +n(B) – n(AB).(***)

Таким образом, подставляя равенства (**) и (***) в (*), получаем: n(A B С)=

=n(A)+n(B)–n(A B)+n(С)–(n(A С)+n(В С)–n(A BС))=

=n(A)+n(B)+n(С)–n(A B)–n(AС)–n(В С)+n(A BС).

Теорема. 3.1 доказана.

Задача 2. Из 28 студентов группы 14 человек занимаются плаванием, 18 человек – баскетболом, 12 студентов – легкой атлетикой, 8 – плаванием и баскетболом, 7 – легкой атлетикой и баскетболом, 6 – плаванием и легкой атлетикой, 3 студентов занимаются и плаванием, и баскетболом, и легкой атлетикой. Сколько в группе студентов, которые не занимаются ни одним из данных видов спорта?

Решение. Анализ условия показывает, что в задаче речь идёт о нескольких множествах. Пусть К – множество студентов группы (n(K)=28), В – множество студентов, занимающихся плаванием (n(B)=14), С – множество студентов, занимающихся баскетболом (n(C)=18), А – множество студентов, занимающихся легкой атлетикой (n(А)=12), М – множество студентов, занимающихся плаванием и легкой атлетикой (n(М)=6), Р – множество студентов, занимающихся баскетболом и легкой атлетикой (n(Р)=7), У – множество студентов, занимающихся плаванием и баскетболом (n(У)=8), L – множество студентов, занимающихся и плаванием, и баскетболом, и легкой атлетикой (п(L)=3).

Изобразим описанную ситуацию с помощью кругов Эйлера (Рис.6). Пусть 1 – множество студентов, которые занимаются и плаванием, и баскетболом, и легкой атлетикой; 2

4

– множество студентов, которые занимаются плаванием и баскетболом, но не занимаются легкой атлетикой; 3 – множество студентов, которые занимаются баскетболом и легкой атлетикой, но не занимаются плаванием; 4 – множество студентов, которые занимаются плаванием и легкой атлетикой, но не занимаются баскетболом.

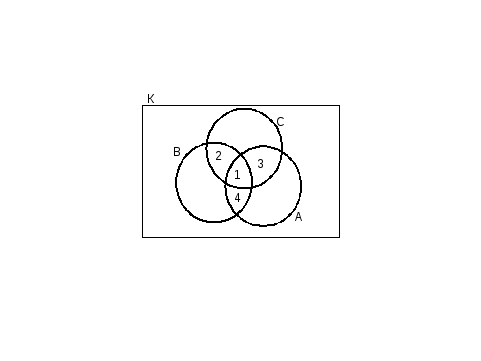Рис.6

Чтобы найти число студентов, которые не занимаются ни плаванием, ни баскетболом, ни легкой атлетикой, необходимо из числа всех студентов группы вычесть число студентов, занимающихся хотя бы одним видом спорта, то есть n(А B C).

По теореме 3.1 имеем

n(А B C)=n(А)+n(B)+n(C)–n(A B)–n(A С)–п(В С)+

+n(A B С)=14+18+12–6–7–8+3=26(студентов).

Так как всего в группе 28 студентов, то не занимаются ни плаванием, ни баскетболом, ни легкой атлетикой: 28–26=2 (студента).

Ответ: 2 студента.