
18
.pdf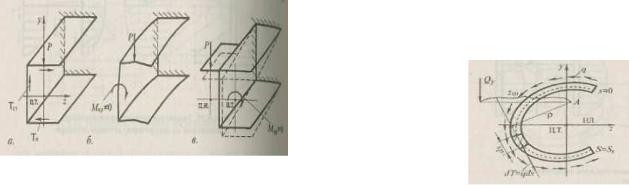
напряжений, а по (8.11) – полный вектор касательных напряжений.
В случае тонкостенного стержня открытого профиля произвольного очертания (см. рис.
8.22) τ определяются по-прежнему по формуле (8.11). Статический момент Sz* (y) отсеченной части сечения будет определяться по формуле
s
S z* (y)= ò ydF * ,
0
где s – координат вдоль контура сечения от свободного края.
§ 8.6. Центр изгиба
Точка плоскости сечения, через которую должна проходить плоскость действия поперечной нагрузки, чтобы изгиб балки не сопровождался кручением, называется центром изгиба или центром жесткости. Геометрическое место центров изгиба поперечных сечений балки называется осью центров изгиба или осью жесткости.
В общем случае точка прохождения равнодействующей касательных усилий (ц.и.) не совпадает с центром тяжести (ц.т.) сечения (см. рис. 8.25в).
Координата ц.и. для открытого контура определяется из условия равенства суммарного момента касательных усилий
dT=qds относительно произвольной точки А
и момента от поперечной силы, например Qу (см. рис. 8.26).
òs |
dTp = Qy zц.и, |
|
|
|
||||
0 |
|
|
|
|
|
|
|
(8.12) |
s |
|
|
|
|
|
|
|
|
òqpds = Qy zц.п |
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
|
1 |
s |
|
|
|
Qy S z* (y) |
|
|
zц.и. = |
|
ò |
qpds, q = |
|
|
|
||
Qy |
J z |
|
||||||
|
|
0 |
|
|
|
|
|
|
|
или |
|
|
|
|
|
||
|
|
|
|
1 |
s |
|
|
|
|
zц.п = |
òSz* (y)pds |
|
|||||
|
J z |
(8.13) |
||||||
|
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
Из формулы (8.13) видно, что положение центра изгиба определяется только геометрической характеристиками поперечного сечения стержня
§8.7. Дифференциальное уравнение изогнутой оси балки
Как было показано в §8.3, мерой деформации стержня при чистом изгибе является кривизна нейтрального слоя, определяемая по формуле (8.6) Как показывает практика, с достаточной для инженерных расчетов точностью этой формулой можно пользоваться и в случае поперечного изгиба стержня. Однако для практических целей кроме кривизны необходимо знать вертикальные перемещения (прогибы) v(х) центров тяжести отдельных сечений и углы поворота этих сечений θ(х) (см. рис. 8.30);
PDF created with pdfFactory Pro trial version www.pdffactory.com

θ(х)—+ при повороте против часовой стрелки, v(х) —+ при перемещении точек балки вверх.
Вследствие гипотезы плоских сечений и относительной малости перемещений v(х) угол поворота сечений θ(х) оказывается равным углу наклона касательной к изогнутой оси балки.
θ (x)= ϕ(x)
При малых углах sin ϕ ≈ ϕ; cosϕ = 1
θ =ν ′ = ddxν = tgϕ ≈ ϕ
Определим форму упругой линии v(х), зная закон изменения ее кривизны. Влияние перерезывающих сил Q на прогибы незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит от величины изгибающего момента (см. формулу 8.6):
k = |
1 |
= |
M z |
(8.18) |
p |
ΕJ z |
С другой стороны, а неподвижной прямоугольной системе координат из дифференциальной геометрии известно, что кривизна плоской кривой будет
|
|
|
|
|
|
|
k = |
ν ′′ |
|
||
|
|
|
|
|
|
|
[1+ (ν ′)2 ]32 |
|
(8.19) |
||
Приравнивая правые части выражений (8.I8) и (8.19), имеем |
|
||||||||||
|
|
ν ′′ |
+ |
|
M z |
|
|||||
|
[1+ (ν ′)2 ]32 |
|
=− |
|
|
|
(8.20) |
||||
|
|
EJ z |
|||||||||
При |
|
малых |
деформациях членом (ν ′)2 можно пренебречь; тогда |
дифференциальное |
|||||||
уравнение (8.20) окончательно примет вид: |
|
||||||||||
ν ′′ =+ |
|
M z (x) |
|
|
|
|
|
|
|
(8.21) |
|
|
− |
|
EJ z |
|
|
|
|
|
|
||
Выражения (8.21) является основой дифференциальным уравнением упругой линии балки при изгибе.
Углы поворота сечений балки θ и перемещения ее точек находят путем последовательного интегрирования соотношения (8.21):
θ =ν ′ = ò |
M (x) |
|
||||||
z |
dx + C, |
|
||||||
EJ z (x) |
(8.22) |
|||||||
|
ò |
|
|
|
M z (x) |
|
|
|
ν = |
dx |
|
|
|
dx + Cx |
+ D |
||
|
|
|
||||||
|
|
ò EJ z (x) |
|
|||||
PDF created with pdfFactory Pro trial version www.pdffactory.com
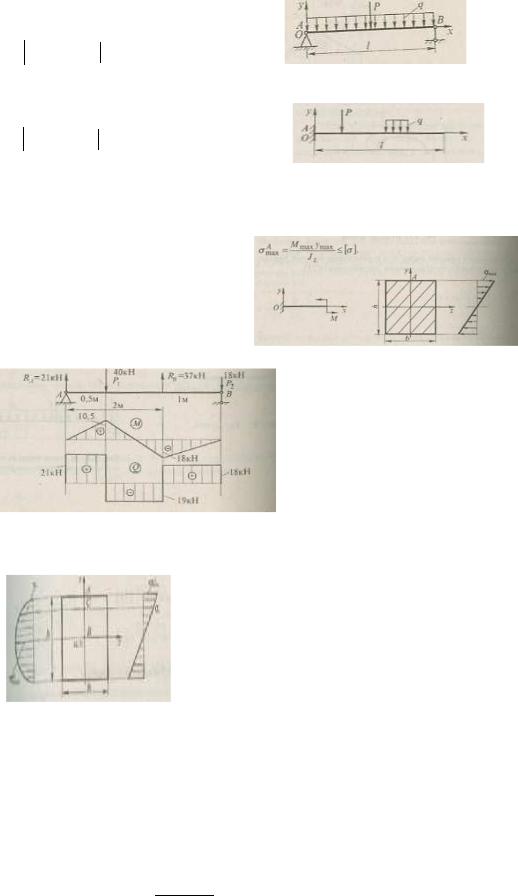
Постоянные С и D определяют из условий закрепления балки (граничных условий).
Граничные условия:
а) балка шарнирно-опертая
ν A x=0 = 0;ν B x=1 = 0
б) балка защемлена
ν A x=0 = 0;θ A x=0 = 0
§8.8 Расчет на прочность при изгибе.
А. Чистый изгиб.
σ maxA = |
M max ymax |
≤ [σ ] |
|
||
|
J z |
|
Б. Поперечный изгиб.
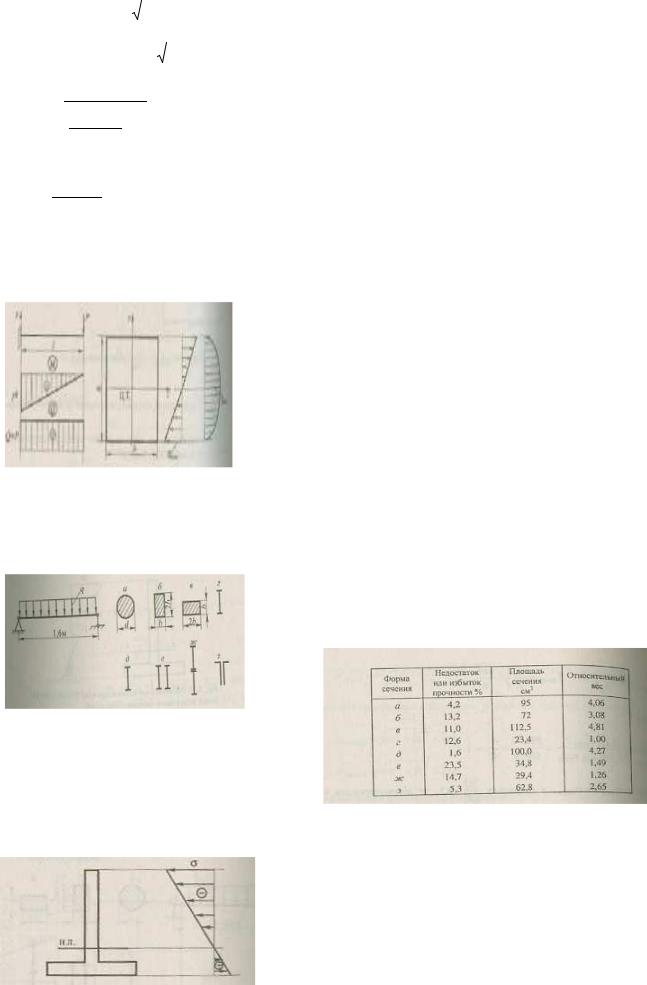
Рассмотрим напряженные состояния в точках А, В и С поперечного сечения(см.рис.. 8.36). Для этого проанализируем эпюры распределения нормальных σ и касательных τ напряжений по высоте балки h (см. рис 8.36).
ТочкаAÞσBmaxA ,τ AB |
=0 |
} |
Одноосные напряженные |
ТочкаBÞτmax ,σ |
=0 |
|
состояния |
Расчет на прочность
σ maxA = |
M max ymax |
£ [σ ],τ maxB |
= |
Qmax Smax* |
£ [τ ] |
|
J z b |
||||
|
J x |
|
|
||
В точке С будет плоское напряженное состояние (действуют напряжения σ c и τ c ).
Главные напряжения, по которым ведется расчет конструкции на прочность рассчитываются по формуле:
σ1,2 = 12 éêëσ ± 
 σ 2 + 4τ 2 ùúû
σ 2 + 4τ 2 ùúû
PDF created with pdfFactory Pro trial version www.pdffactory.com
Критерии прочности для плоского напряженного состояния приобретают вид:
|
|
|
|
1 |
é |
|
|
|
|
|
|
ù |
£ [σ ], |
||
|
|
|
|
|
|
2 |
|
|
2 |
||||||
σ эквI |
= σ 1 |
= |
|
|
êσ + σ |
|
+ 4τ |
ú |
|||||||
2 |
|
||||||||||||||
|
|
|
|
ë |
|
|
|
|
|
û |
|
|
|||
|
|
1− μ |
|
1+ μ |
|
|
|
≤ [σ ], |
|||||||
σ эквII |
= |
σ + |
|
|
σ 2 + 4τ 2 |
||||||||||
|
2 |
|
|||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
μ = 1 для пластичных материалов, μ = 0,8 для хрупких материалов, σ эквIII = 
 σ 2 + 4τ 2 ≤ [σ ],
σ 2 + 4τ 2 ≤ [σ ],
σэквIV = 
 σ 2 + 3τ 2 ≤ [σ ].
σ 2 + 3τ 2 ≤ [σ ].
Сечение балки подбирается по формуле
W ³ M[max] z σ
§8.9. Рациональные формы сечений балочных
конструкций
Оценим порядок и на примере консольной балки, показанной на рис. 8.37.
M max = Pl, Qmax = P; |
|
|
|
|
|
|
|
|
||||||
σ max = |
M |
max |
y |
max |
; ymax = |
|
h |
, J z = |
bh3 |
|
|
|
|
|
|
J z |
|
2 |
12 |
|
[τ ] |
|
|
||||||
|
|
|
|
|
|
|
||||||||
Отсюда |
τ max << σ max , |
а поскольку |
≈ 0,5 то |
|||||||||||
[σ ] |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
доминирующим в этом, случае будет расчет по нормальным напряжениям и условие прочности будет
выглядеть так:
σ max = |
M z max |
≤ [σ ] |
|
||
|
Wz |
|
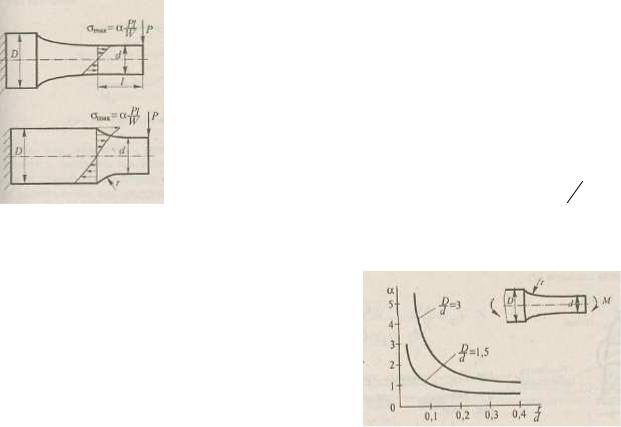
Для примера ниже приведены данные по рациональному выбору форме сечения балки исходя из расчета ее на прочность (см. рис. 8.38).
Исходные данные: нагрузка ql=100кН, материал ст.3,[σ]=160Мпа.
Результаты расчетов сведены в таблицу.
А
нализ
данных
таблиц ы показывает что с позиций массовой характеристики при таком виде нагружения наиболее рациональной является двухтавровая форма сечения балки, нагруженной со стороны полки. Этот вывод
справедлив для любой балка, работающей на плоский изгиб и изготовленной из пластичного материала.
Для балок из хрупких материалов, так как [σ ] + <[σ ] − , симметричные сечения не являются
рациональными.
Рациональной здесь является несимметричная форма сечения балки (см рис 8.39).
PDF created with pdfFactory Pro trial version www.pdffactory.com
§8.11. Концентрации напряжений при изгибе
При изгибе, как и при растяжения или кручении, в местах резкого изменения формы или размеров поперечных сечений наблюдается концентрация напряжений (см.
рис. 8.45).
Для конструкций. выполненных из пластичного материала. при статическом нагружения благодаря перераспределению напряжений концентрация напряжений не опасна. Что нельзя сказать о конструкциях. выполненных из хрупкого материала:
σ ном = |
M |
;σ max = ασ ном |
|
0,1d 3 |
|||
|
|
На рис. 8.46 для примера показано изменение коэффициента концентрации напряжений α в зависимости от
отношения радиуса галтели r к диаметру образца d ( r d ) для
различных соотношений D/d.
Как видим, чем плавне меняется форма или размеры поперечного сечения, тем меньше коэффициент концентрации.
PDF created with pdfFactory Pro trial version www.pdffactory.com

Устойчивость сжатых стержней в упругой области
§13.1. Понятие об устойчивости
На рис. 13.1 показаны четыре формы равновесия механической системы.
Равновесное состояния деформируемой системы, например. стержня также может быть устойчивым рис. 13.2а. безразличным (критическим рис. 13.2б и неустойчивым (рис. 13.2в).
Строгое определение устойчивости по теореме Пуанкаре звучит так. Пусть идеально прямой стержень нагружен строго центрально продольной силой Р< Р кр (рис. 13.3). При таких
предложениях прямолинейная форма стержня всегда будет являться возможной формой равновесия. Об устойчивости этой формы равновесия стержня можно судить по реакции ее
на поперечную нагрузку Р1 , которая вызовет прогиб стержня. При отсутствии силы Р малая P1 вызовет малый прогиб стержня. При небольшой силе Р положение стержня не
изменится, а равновесие его сохранится устойчивым.
Равновесие стержня устойчиво, если задавшись любой величиной прогиба ƒ>0,
всегда можно указать такую конечную величину возмущения ε>0, что при |
|
P1 |
|
< ε |
|
|
величина прогиба ни в одной точке системы не достигнет величины ƒ, т.е. будет ν < f
В механике деформируемого твердого тела для оценки устойчивости используется обычно анализ поведения конструкции при статическом нагружении.
Под устойчивостью понимается свойство системы при любом малом отклонении от состояния равновесия стремиться к своему первоначальному равновесному состоянию и возвращаться к нему после снятия внешнего воздействия.
Если система не возвращается после снятия возмущения к своему исходному состояния равновесия, то она называется н е у сто й ч и в о й.
Нагрузка, при которой начальная (исходная) форма равновесия системы перестает быть устойчивой, называется к р и т и ч е с к о й. Приложение к стержню силы
P = Pкр или P > Pкр вызывает его продольный и з г и б; это потеря устойчивости первого
рода.
§13.2. Критическая нагрузка для сжатого стержня, шарнирно опертого по концам. Формула Эйлера.
Определим критическую нагрузку для шарнирного оперного стержня с прямой осью и постоянным по длине l поперечным сечением площадью F (см рис. 13.4)
Дифференциальное уравнение изогнутой оси стержня будет
ΕJ |
d 2ν |
= M (x) |
|
dx2 |
|||
|
(13.1) |
PDF created with pdfFactory Pro trial version www.pdffactory.com

Изгибающий момент в произвольном сечении стержня равен
M (x)= -Pν (x) (13.2)
С учетом (13.2) выражение (13.1) примет форму
EJ d 2ν (x) = -Pν (x) dx2
или
d 2ν (x) + k 2ν (x) = 0 dx2
где k 2 = EJP
Общее решение дифференциального уравнения (13.3) можно Записать в виде
(13.3)
(13.4)
ν = c1 sin kx + c2 cos kx |
|
(13.5) |
||||
где c1 и c2 — произвольные постоянные. |
|
|
||||
Решение (13.5) должно удовлетворять граничным условиям |
|
|
||||
ν |
|
x=0 = 0;ν |
|
x=l = 0 |
|
(13.6) |
|
|
|
||||
|
|
|||||
При х=0 прогиб ν (0) = 0 ; из (13.5) получаем c2 = 0 значит ν (х)=с1 sin kx . |
|
|||||
При х=l прогиб ν ( l )=0. поэтому c1 sin kl = 0 . Здесь c1 ¹ 0 , |
так как при |
c1 = 0 прогиб |
||||
вообще отсутствует, т. е. стержень не теряет устойчивость. |
Следовательно, при c1 ¹ 0 |
|||||
sin kl = 0 . Корни этого трансцендентного уравнения будут kl Þ 0,π ,2π ,..., nπ |
; отсюда |
|||||
kl = nπ;n = 0,1,2,3... |
|
(13.7) |
||||
|
|
|||||
Отбрасывая решение kl = 0 , как отвечающее прямолинейному состояния стержня, а не изогнутому, из (13.7) находим
|
|
|
|
k = |
nπ |
|
|
|
(13.8) |
||
|
|
|
|
|
|
l |
|
|
|
|
|
Используя равенства (13.4) и (13.8) |
можно записать. |
||||||||||
k |
2 |
= |
n2π 2 |
= |
P |
; n = 1,2,3... |
|
||||
|
|
l 2 |
EJ |
|
|||||||
|
|
|
|
|
|
|
|
|
|||
Из (13.9) имеем |
|
||||||||||
Pкр = |
|
n2π 2 EJ min |
(13.10) |
||||||||
|
|
l2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
Из анализа (13.10) вытекает, что имеется бесчисленное множество Pкр , при которых
могут существовать изогнутые формы равновесия стержня (см. рис. 13.5). Наименьшее значение сжимающей критической силы (реализуемой) соответствует n = 1
Функция прогиба ν (х) |
будет ν (х)= c sin kx = c sin |
nπ |
x , |
|
|
||||
|
1 |
1 |
l |
|
|
|
|
|
|
где c1 = f - амплитуда |
прогиба (или |
стрела). При |
||
PDF created with pdfFactory Pro trial version www.pdffactory.com

n = 1 имеем
ν (x) = f sin |
πx |
|
|
(13.11) |
|
l |
|
||||
|
|
|
|||
Pкр = |
π 2EJ min |
Þ формула Эйлера |
(13.12) |
||
l 2 |
|
|
|||
|
|
|
|
|
|
Таким образом, прямолинейная форма равновесия стержня оказывает устойчивой при Р < Р и неустойчивой при P > Pкр
Отметим. что уравнение (13.3) составлено для стержня в деформированном состоянии. Это уже в принципе отказ от линейной постановки задачи, при которой деформированное и недеформированное состояния при составлении уравнений равновесия не должны различаться (принимая начальных размеров). Таким образом, модель (13.3) является приближенной. Она позволяет найти критическую силу (13.12) и прогиб (13.11) при не дает возможности описать состояние системы. Для этого надо привлечь точное
уравнение изгиба
|
|
|
d 2ν |
|
|
|
|
Pν |
|
||
|
|
|
dx2 |
|
|
|
|
= - |
(13.13) |
||
é |
æ dν ö2 |
ù |
3 |
2 |
EJ |
||||||
|
|
|
|
||||||||
ê1 |
+ ç |
|
|
÷ |
ú |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ê |
è |
|
dx ø |
ú |
|
|
|
|
|
||
ë |
|
|
|
|
|
û |
|
|
|
|
|
и уточненные граничные условия при х= l, так как вследствие изгиба стержня происходит
смещение опоры на величину |
(см. рис. 13.4б). |
|||||||||||||||||||||||||
|
l |
|
|
|
|
l |
é |
|
|
|
|
|
|
|
|
|
|
|
ù |
|
|
l |
|
|
|
|
|
(ds - dx)= |
|
|
æ dν ö |
2 |
|
1 |
æ dv ö |
2 |
|||||||||||||||||
|
ò |
ò |
êdx 1+ |
|
- dxú |
|
|
|
||||||||||||||||||
D = |
ç |
|
|
÷ |
|
= |
|
|
ç |
|
÷ dx |
|||||||||||||||
|
|
|
2 |
|
|
|||||||||||||||||||||
|
|
|
|
ê |
|
|
|
|
|
è |
dx ø |
|
ú |
|
òè dx ø |
|
||||||||||
|
0 |
|
|
|
0 |
ë |
|
|
|
|
|
|
|
|
|
|
|
û |
|
|
0 |
|
|
|
|
|
Точное решение уравнения (13.13) с учетом граничного условия ν (l - D) = 0 дает |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
f |
|
|
2 |
|
|
|
1- |
|
Pкр |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
= |
2 |
|
|
|
|
|
|
|
|
(13.14) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|||||||
|
|
|
l |
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где f =ν max —стрела прогиба. Так, например, если P =1,05Pкр , т.е. всего на 5 %; . f = 0,21,
составит 1/5 длины стержня.
§13.3. Влияние условий закрепления концов стержня на величину критической силы
Рассмотрим влияние граничных условий на величину критической силы на примере консольного стержня (см. рис. 13.6).
Сила Р сохраняет вертикальное положение при деформации стержня (см. рис.13.6)
Дифференцируя уравнение (13.3) дважды по х,
представляем его в виде |
|
||||
|
d 4ν |
+ k 2 |
d 2 v |
= 0 |
(13.15) |
|
dx4 |
dx2 |
|||
|
|
|
|
||
Интеграл уравнения (13.15) будет |
|
|
|
(13.16) |
|
ν = A sin kx + B cos kx + Cx + D |
|
|
|
||
где A, B, C, D — константы, которые находятся путем использования граничных условий. Выпишем граничные условия:
PDF created with pdfFactory Pro trial version www.pdffactory.com

ν |
x=0 |
= 0, |
dv |
|
|
x=0 = 0 |
||||||
|
||||||||||||
dx |
||||||||||||
|
|
|
|
|
|
d 2ν |
(13.17) |
|||||
|
|
|
|
|
|
|
||||||
M |
x=l = −ΕJ |
= 0;Q |
x=l = P |
dv |
|
|||||||
2 |
dx |
|||||||||||
|
|
|
|
|
|
|
dx |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Определяя константы А, В, С, D и рассуждая также, как и в предыдущем параграфе, находим
Pкр = |
π 2 EJ min |
(13.18) |
|
4l 2 |
|||
|
|
Сравнивая формулы (13.12) и (13.18). видим, что для консольного стержня той же длины, оказалось в четыре раза меньше. Очевидно, критическая сила для защемленного одним концом стержня длины l будет равна критической силе шарнирно закрепленного стержня, имеющего длину
длину 2l (см. рис. 13.7).
Используя особенности упругой линии, можно довольно легко распространить полученное решение на другие случаи закрепления стержней. Обобщая полученные результаты, запишем обобщенную формулу Эйлера
Pкр |
= |
π 2 |
ΕJ min |
(13.19) |
|
(μl)2 |
|||||
|
|
|
|||
где µ — коэффициент приведения длины. показывающий. насколько надо изменить длину шарнирно опертого стержня, чтобы Р,, для него равнялось
стержня длиной l при заданных граничных условиях (или условиях закрепления).
На рис. 13.8 показаны различные случаи закрепления стержня и указаны соответствующие значения коэффициента µ
§ 13.4. Критические напряжения
Используя формулу (13.19), найдем критические напряжения
|
|
|
|
|
|
|
|
σ кр = |
Pкр |
= |
π 2ΕJ min |
|
|
|
|
|
F |
(μl)2 F |
|||||
|
|
|
|
|
|
|
|
|
|
||
где imin |
= |
|
|
J min |
|
- радиус инерции сечения стержня. |
|||||
|
|
|
|||||||||
|
|
|
|
|
|
F |
|
|
|
||
С учетом (13.21) получаем |
|
|
|
||||||||
σ кр = |
π 2Ε |
|
|
|
|
|
|
|
|||
|
λ2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
где λ = |
μl |
|
- гибкость стержня. |
|
|
|
|||||
imin |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
(13.20)
(13.21)
(13.22)
PDF created with pdfFactory Pro trial version www.pdffactory.com
§ 13.5.Пределы применимости формулы Эйлера
Формула Эйлера (13.22) справедлива при условии, что деформация сжатия подчиняется закону Гука; иными словами σкр не должно превышать σпц для данного материала
σ кр £ σ пц |
(13.23) |
С учетом (13.22) условие (13.23) примет вид
πλ22E £ σ пц
Отсюда
λпр = π |
Ε |
(13.24) |
σ пц |
где λпр — предельное значение гибкости стержня, являющееся константой материала
стержня.
Условие применимости формулы Эйлера σ кр £ σ пц
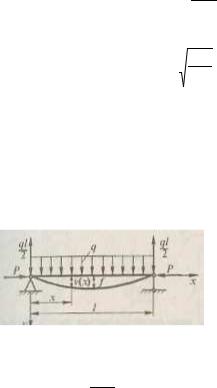
§13.7. Продольно-поперечный изгиб стержня
Для этого случая нагружения стержня (см. рис. 13.11) дифференциальное уравнение изогнутой его оси будет иметь вид
EJ |
d 2ν |
= -Pν - ql x + qx2 |
||
dx2 |
||||
|
2 |
2 |
||
Дифференцируя дважды уравнение (13.40), получаем
EJ d 4ν + P d 2ν = q dx4 dx2
Аппроксимационную функцию ν (x) выберем в виде
(13.40)
(13.41)
ν = f sin |
πx |
|
|
|
|
|
|
|
|
|
(13.42) |
l |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
Составим уравнение Бубнова – Галеркина |
|
||||||||||
l |
æ |
|
4 |
|
d |
2 |
ö |
|
|
|
|
|
ç |
|
d ν |
+ P |
|
ν |
÷ |
πx |
dx = 0 |
(13.43) |
|
òçEJ |
dx |
dx |
2 |
- q÷ sin |
l |
||||||
0 |
è |
|
|
|
ø |
|
|
||||
Подставляя в уравнение (13.43) выражение (13.42) и интегрируя его, имеем
|
|
4 |
|
|
|
ql 4 |
|
|
|
|
|||||
f = |
|
π 5 |
|
EJ |
|
|
|
|
|
(13.44) |
|||||
|
|
|
Pl 2 |
|
|
|
|
||||||||
|
|
1- |
|
|
|
|
|
|
|||||||
|
|
π 2EJ |
4 |
|
ql 4 |
|
|||||||||
|
|
|
|
|
|
|
|
||||||||
Обозначим через fп = |
|
Þ приближенное значение стрелы прогиба при действии |
|||||||||||||
π 5 |
|
EJ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
одной поперечной нагрузки. Тогда формулу (13.44) перепишем в виде |
|||||||||||||||
f = |
|
f п |
|
|
|
|
|
|
|
(13.45) |
|||||
|
|
|
|
P |
|
|
|
|
|
|
|
|
|||
1- |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
P |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
кр |
|
|
|
|
|
|
|
|
||
PDF created with pdfFactory Pro trial version www.pdffactory.com
