Teoriya_veroyatnostey_Nosovskaya

31

П р и м е р 32. В урне содержатся белые и черные шары в отношении 4:1. После извлечения шара регистрируется его цвет, и шар возвращается в урну. Чему равно наименьшее число извлечений n, при котором с вероятностью 0,95 можно ожидать, что абсолютная величина отклонения относительной частоты появления белого шара от его вероятности будет не более чем

0,01?

Р е ш е н и е.

Необходимо найти n. По формуле (22) получим

По таблице (приложение 1) находим 0, 475 = F (1, 96) . Тогда

0, 025 × n = 1, 96;

n = 78, 4;

n » 6147.

Таким образом, искомое число извлечений n ≈ 6147 .♦

П р и м е р 33. Вероятность появления случайного события в каждом из 900 независимых экспериментов равна 0,75. Каким должно быть значение ε > 0 , чтобы с вероятностью 0,99 можно ожидать, что абсолютная величина отклонения относительной частоты появления случайного события от его вероятности будет не более чем ε ?

Р е ш е н и е. По условию задачи:

найти ε . По формуле (22):

32

Φ (69,3ε ) = 0, 495 .

По таблице (приложение 1) находим 0, 495 = Φ (2, 74) . Тогда

69, 3ε = 2, 74;

ε ≈ 0, 04.

Таким образом, условию задачи удовлетворяет значение

ε ≈ 0, 04 .♦

НАИВЕРОЯТНЕЙШЕЕ ЧИСЛО ПОЯВЛЕНИЙ СОБЫТИЯ В НЕЗАВИСИМЫХ ИСПЫТАНИЯХ

Число k0 (наступления события в независимых испытаниях, в каждом из которых вероятность появления события равна p) называется наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях k0 раз, превышает (или, по крайней мере, не меньше) вероятности остальных возможных исходов испытаний.

Наивероятнейшее число k0 определяют из неравенства:

0и k0+1;

3)если число np - целое, то наивероятнейшее число k0 = np .

Пр и м е р 34. Вероятность того, что посеянное зерно ячменя прорастет в лабораторных условиях, в среднем равна 0,9. Было посеяно 700 зерен ячменя в лабораторных условиях. Найти наивероятнейшее число зерен, которые прорастут, и найти вероятность этого числа.

Р е ш е н и е.

По условию задачи n = 700; p = 0, 9; q = 0,1. Наивероятнейшее число проросших зеренопределимизнеравенства (23):

700 ×0,9 - 0,1 £ k0 < 900 ×0,9 + 0,9; 729,9 ≤ k0 < 630,9;

k0 = 630.

33

Найдем вероятность, что из посеянных 700 зерен прорастут ровно 630. Для этого воспользуемся локальной теоремой Лапласа:

= 630 - 700 ×0, 09 =

Определим x 0 .

700 × 0, 9 × 0,1

По таблице (приложение 2) найдем ϕ (0) = 0, 3989 , тогда

П р и м е р 35. Вероятность появления события в каждом из независимых испытаний равна 0,3. Найти число испытаний n, при котором наивероятнейшее число появлений события в этих испытаниях будет равно 30.

Р е ш е н и е.

По условию k0 = 30; p = 0,3; q = 0, 7. Необходимо найти n. Воспользуемся неравенством (23):

n ×0,3 - 0, 7 £ 30 < n × 0,3 + 0,3;

0,3n - 0, 7 £ 30 < 0,3n + 0,3.

Получим систему неравенств для определения неизвестного числа n:

Итак, искомое число испытаний должно удовлетворять двойному неравенству: 100 ≤ n ≤ 102 .♦

П р и м е р 36. Чему равна вероятность p наступления события в каждом из 39 независимых испытаний, если наивероятнейшее число наступлений события в этих

Воспользуемся неравенством (23) и тем, что q = 1 − p :

35

n(∞)

∑ pi = 1.

i=1

Пр и м е р 37. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.

Р е ш е н и е.

Дискретная случайная величина Х (число отказавших элементов

водном опыте) имеет следующие возможные значения: х1=0 (ни один из элементов устройства не отказал), х2=1 (отказал один элемент), х3=2 (отказали два элемента) и х4=3 (отказали три элемента). Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что по условию n=3; p=0,1 (следовательно, q=1–0,1=0,9), получим:

P3 (0) = q3 = 0, 93 = 0, 729 ;

P3 (1) = C31 pq2 = 3× 0,1× 0, 92 = 0, 243 ; P3 (2) = C32 p2 q = 3 ×0,12 × 0, 9 = 0, 027 ; P3 (3) = p3 = 0,13 = 0, 001 .

К о н т р о л ь: 0,729 + 0,243 + 0,027 + 0,001 = 1.

Напишем искомый закон распределения дискретной случайной величины Х:

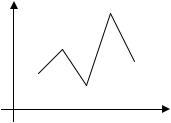
Графически закон распределения дискретной случайной величины можно представить в виде

многоугольника распределения – ломаной,

соединяющей точки плоскости с координатами

(xi, pi).

Рисунок 2

36

Для дискретной случайной величины значение функции распределения F(x) в каждой точке представляет собой сумму вероятностей тех ее возможных значений, которые меньше аргумента функции.

П р и м е р 38. Дан ряд распределения дискретной случайной величины Х

Найти и изобразить графически ее функцию распределения.

Ре ш е н и е.

1)Если x ≤ 1 , то F(x)=0 (в том числе и при x=1 F(1)=P(X<1)=0).

2)Пусть 1 < x ≤ 4 ; F(x)=P (X = 1)=0,4.

3)Пусть 4 < x ≤ 5 ; F(x)=P(X<x)=P(X=1) + P(X=4)=0,4 + 0,1=0,5.

4)Пусть 5 < x ≤ 7 ; F(x)=P(X<x)=P(X=1) +P(X=4) + P(X=5)=0,4+

+0,1 + 0,3=0,8.

5)Пусть x > 7 ; F(x)=P(X=1) + P(X=4) + P(X=5) + P(X=7)=0,4 +

+0,1 +0,3 + 0,2=1.

Итак,

1, при x > 7.

График функции F(x) изображен на рис. 3.

1 F(x)

0,9

0,8

0,7

0,6

0,5

0,4

Рисунок 3

37

♦

Для задания закона распределения непрерывной случайной величины используется плотность распределения вероятностей (дифференциальная функция распределения).

Функция f(x), называемая плотностью распределения вероятностей непрерывной случайной величины, определяется по формуле:

то есть является производной функции распределения.

П р и м е р 39. Дана функция распределения непрерывной случайной величины Х:

Найти функцию плотности распределения f(x). Р е ш е н и е.

По определению

Если известна плотность распределения вероятностей f(x), то можно найти функцию распределения F(x) по формуле:

−∞

Поэтому функция распределения непрерывной случайной величины также называется интегральной функцией распределения.

ОСНОВНЫЕ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

40

Сумма вероятностей всех возможных значений дискретной

3

случайной величины равна единице: ∑ pi = 1 или 0, 2 + 0, 3 + p3 = 1 .

Для отыскания x2 необходимо составить уравнение. Запишем выражения для М(Х) и D(X):

M ( X ) = 1×0,3 + x2 × 0, 2 + 3× 0, 5 = 0, 2x2 +1,8 ; D ( X ) = 12 ×0, 3 + x22 ×0, 2 + 32 × 0, 5 - (0, 2x2 +1,8)2 =

= 4,8 + 0, 2x22 - 0, 04x22 - 0, 72x2 - 3, 24 = 0,16x22 - 0, 72x2 +1,56.

По условию D(X)=0,76. Подставив это значение, получим и решим уравнение:

0,16x22 - 0, 72x2 +1, 56 = 0, 76; 0,16x22 - 0, 72x2 + 0,8 = 0 ¸ 0, 08; 2x22 - 9x2 +10 = 0;

x2(1) = 2, x2(2) = 5 .

2

По условию х1<х2<х3 и случайная величина принимает целые значения, поэтому задаче удовлетворяет лишь x2(1) = 2 .

Таким образом, искомый закон распределения

Математическое ожидание будет равно:

M ( X ) = 0, 2x2 +1,8 = 0, 2 × 2 +1,8 = 2, 2 .♦

Средним квадратическим отклонением σ случайной величины Х называется квадратный корень из дисперсии: