
Teoriya_veroyatnostey_Nosovskaya
.pdf
21
5)ABC + ABC + ABC + ABC –« произошли события А и В или произошли события А и С или произошли события В и С или произошли события А и В и С»;
6)ABC + ABC + ABC –« произошло событие А и не произошли события В и С или произошло событие В и не произошли события А и С или произошло событие С и не произошли события А и В»;
7)ABC + ABC + ABC –« произошли события А и В и не произошло событие С или произошли события А и В и не произошло событие С или произошли события В и С и не произошло событие А»;
8)ABC –« не произошло событие А и не произошло событие В и не произошло событие С» - совместное непоявление событий
A , B и C .
П р и м е р 22. Устройство состоит из трех элементов, работающих независимо. Вероятности безотказной работы (за время t) первого, второго и третьего элементов соответственно равны 0,6; 0,7; 0,8. Найти вероятности того, что за время t безотказно будут работать: а) все три элемента; б) только два элемента; в) только один элемент.
Р е ш е н и е.
а) Пусть событие А={за время t безотказно будут работать все три элемента}. Введем обозначения событий:
В1={за время t безотказно будет работать первый элемент}; В2={за время t безотказно будет работать второй элемент}; В3={за время t безотказно будет работать третий элемент}. Вероятности событий В1, В2 и В3 равны:
P ( B1 ) = 0, 6; P ( B2 ) = 0, 7; P ( B3 ) = 0,8.
Событие А состоит в совместном появлении событий В1, В2 и В3, т.е.
A = B1 B2 B3 .
По условию задачи события В1, В2 и В3 независимы, поэтому
P ( A) = P (B1 B2 B3 ) = P ( B1 ) P ( B2 ) P ( B3 ) = 0, 6 ×0, 7 ×0,8 = 0, 336.
б) Пусть событие С={за время t безотказно будут работать только два элемента}. Введем обозначения событий,

22
противоположных к событиям В1, В2 и В3: B1 ={за время t откажет первый элемент}; B2 ={за время t откажет второй элемент}; B3 ={за время t откажет третий элемент}.
При этом
P (B1 ) = 1- P ( B1 ) = 1- 0, 6 = 0, 4; P (B2 ) = 1- P ( B2 ) = 1 - 0, 7 = 0,3;
P (B3 ) = 1- P ( B3 ) = 1 - 0,8 = 0, 2.
Событие С состоит в том что будут работать или только первый и второй элементы и не будет работать третий, или только первый и третий элементы и не будет работать второй, или только второй и третий элементы и не будет работать первый. Таким образом,
C = B1 B2 B3 + B1 B2 B3 + B1B2 B3
События B1 B2 B3 , B1 B2 B3 и B1 B2 B3 несовместны, значит
P (C ) = P (B1 B2 B3 + B1 B2 B3 + B1 B2 B3 ) = P (B1 B2 B3 ) + P (B1 B2 B3 ) + P (B1 B2 B3 ); P (C ) = P ( B1 ) P ( B2 ) P (B3 ) + P ( B1 ) P (B2 )P ( B3 ) + P (B1 )P ( B2 ) P ( B3 );
P (C ) = 0, 6 ×0, 7 ×0, 2 + 0, 6 × 0, 3× 0,8 + 0, 4 ×0, 7 × 0,8 = 0, 084 + 0,144 + 0, 224 = 0, 452.
в) Пусть событие D={за время t безотказно будет работать только один элемент}. Событие D состоит в том, что или будет работать первый элемент и не будут работать второй и третий элементы, или будет работать второй элемент и не будут работать первый и третий элементы, или будет работать третий элемент и не будут работать первый и второй элементы. Таким образом,
D = B1 B2 B3 + B1 B2 B3 + B1 B2 B3
События B1 B2 B3 , B1B2 B3 и B1 B2 B3 несовместны, значит
P ( D) = P (B1 B2 B3 + B1 B2 B3 + B1 B2 B3 ) = P (B1 B2 B3 ) + P (B1B2 B3 )+ P (B1 B2 B3 ); P ( D) = P ( B1 ) P (B2 )P (B3 ) + P (B1 )P ( B2 ) P (B3 ) + P (B1 )P (B2 )P ( B3 );
P ( D) = 0, 6 × 0, 3× 0, 2 + 0, 4 ×0, 7 × 0, 2 + 0, 4 ×0,3× 0,8 = 0, 036 + 0, 056 + 0, 096 = 0,188.
♦

23
ВЕРОЯТНОСТЬ ПОЯВЛЕНИЯ ХОТЯ БЫ ОДНОГО СОБЫТИЯ
Пусть A1 , A2 ,..., Ak - независимые события, причем известны вероятности этих событий P ( A1 ) , P ( A2 ) ,..., P ( Ak ).
Тогда вероятность события А, состоящего в появлении хотя бы одного из событий A1 , A2 ,..., Ak , равна разности между единицей
и произведением вероятностей противоположных |
событий |
||||||||||||
|
|
, |
|
,..., |
|
: |
|
|
|
|
|
|
|
|
A1 |
A2 |
Ak |
|
|||||||||
|
|
|
|
|
|
P ( A) = 1- P ( |
|
) P ( |
|
) P ( |
|
) |
(13) |
|
|
|
|
|
|
A1 |
A2 |
Ak |
|||||
В частном случае, если вероятности независимых событий равны, т.е. P ( A1 ) = P ( A2 ) = ... = P ( Ak ) = p , то вероятность события
А равна |
|
P ( A) = 1- (1 - p )k |
(14) |
(вэтомслучае P ( A1 )P ( A2 ) P ( Ak ) = (1 - p )(1 - p) (1 - p ) = (1 - p)k ).
k раз
П р и м е р 23. Два охотника стреляют в волка, причем каждый из них делает один выстрел. Для первого охотника вероятность попадания равна 0,7, для второго – 0,8. Найти вероятность попадания в волка хотя бы одним охотником.
Р е ш е н и е.
Пусть событие А={попадание в волка хотя бы одним
охотником}. |
Обозначим |
события: A1 ={попадание |
в |
волка |
||
первым охотником}, |
A2 ={попадание |
в |
волка |
вторым |
||
охотником}. |
P ( A1 ) = 0, 7 , P ( A2 ) = 0,8 . |
По |
формуле |
(13) |
||
вероятность попадания в волка хотя бы одним охотником будет равна:
P ( A) = 1- P (A1 )P ( A2 ) = 1- (1 - 0, 7)(1 - 0,8) = 1 - 0, 3 ×0, 2 = 0, 94. ♦
П р и м е р 24. Среди билетов денежно-вещевой лотереи половина выигрышных. Сколько лотерейных билетов нужно купить, чтобы с вероятностью, не меньшей 0,999, быть уверенным в выигрыше хотя бы по одному билету?

24
Р е ш е н и е.
Пусть событие А={выигрыш хотя бы по одному билету}. Обозначим события Ai ={выигрыш по i-му билету}. Пусть
вероятность события Ai равна P ( Ai ) = p . Тогда вероятность
выигрыша хотя бы по одному из n приобретенных билетов по формуле (14) равна
P ( A) = 1- (1 - p)n .
По условию 1 - (1 - p)n ³ P ,где P = 0, 999 откуда
(1 - p )n £ 1 - P.
Логарифмируя обе части неравенства, имеем n lg (1- p ) £ lg (1- P) .
Учитывая, что lg (1- p ) - величина отрицательная, получим
lg (1 - P) |
(15) |
n ³ lg (1 - p ) . |
По условию p = 0,5, P = 0,999 . По формуле (15)
³ lg 0, 001 »
n 10 , lg 0,5
т.е. необходимо купить не менее 10 лотерейных билетов.♦
ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ ФОРМУЛЫ БАЙЕСА
Если событие А может наступить только при появлении одного из несовместных событий (гипотез) Н1, Н2,…, Нn, образующих полную группу, то вероятность события А вычисляется по формуле полной вероятности:
n |
|
P ( A) = ∑ P ( Hi ) × P ( A / Hi ) , |
(16) |
i =1 |
|
где P(Hi) – вероятность гипотезы; |
P(A/Hi) – условная |
|
n |
вероятность события А при этой гипотезе; |
∑ P(Hi ) = 1. |
|
i =1 |
П р и м е р 25. Путник должен попасть из пункта В в пункт А в соответствии со схемой дорог (рис. 1). Для этого он

25
должен пройти один |
|
|
|
|
|
||
из промежуточных |
|
H1 |
|
A |
|||
пунктов |
H1, H2 или |
|
|
||||
|
|
H2 |
|||||
H3.Выбор |
любой |
В |
|
||||
|
|
|
|
||||
дороги |
в |
любом |
|
|
H3 |
|
|
пункте |
|
|
|
|
|
||
равновозможен. |
|
|
|
|
|
||
Найти |
вероятность |
|
|
|
|
|
|
достижения |
|
|
|
|
|
|
|
путником намеченной цели.
Рисунок 1
Р е ш е н и е.
Пусть событие А={достижение путником намеченной цели}. Для того чтобы попасть в пункт А, путник должен пройти один из промежуточных пунктов H1, H2 или H3. Будем считать
гипотезами |
H1={выбран |
промежуточный |
пункт |
H1}, |
||
H2={выбран промежуточный пункт H2}, H3={выбран |
||||||
промежуточный |
пункт |
H3}. |
Вероятности |
гипотез |
||
P(H1)=P(H2)=P(H3)=1/3. Найдем условную вероятность события А при реализации каждой гипотезы. Например, появление H1 означает, что есть два равновозможных исхода (из пункта H1 выходят две дороги), из которых лишь один благоприятствует событию А, т.е.
P( А/ Н1 ) = 1 . 2
Аналогично определяем, что P( А/ Н2 ) = 1 , P( А/ Н3 ) = 0. 4
Согласно формуле (16) полной вероятности, получаем
P( А) = 1 × 1 + 1 × 1 + 1 × 0 = 1 . ♦ 3 2 3 4 3 4
Пусть известен результат опыта, а именно то, что произошло событие А. Этот факт может изменить априорные (то есть известные до опыта) вероятности гипотез. Для переоценки вероятностей гипотез при известном результате опыта используются формулы Байеса:

26
P(Нi |
/ A) = |
P(Hi )P( A / Hi ) |
. |
(17) |
|
||||
|
|
P( A) |
|
|
П р и м е р 26. После двух выстрелов двух стрелков, вероятности попаданий которых равны 0,6 и 0,7, в мишени оказалась одна пробоина. Найти вероятность того, что попал первый стрелок.
Р е ш е н и е.
Пусть событие А– одно попадание при двух выстрелах, а гипотезы: Н1– первый попал, а второй промахнулся, Н2– первый промахнулся, а второй попал, Н3– оба попали, Н4– оба промахнулись. Вероятности гипотез:
P(Н1)=0,6·0,3=0,18, P(Н2)=0,4·0,7=0,28, P(Н3)=0,6·0,7=0,42,
P(Н4)=0,4·0,3=0,12.
Тогда P(А/Н1)=P(А/Н2)=1, P(А/Н3)=P(А/Н4) = 0.
Следовательно, полная вероятность
P(А)=0,18·1+0,28·1+0,42·0+0,12·0=0,46.
Применяя формулу Байеса, получим:
P(Н1 |
/ А) = |
0,18 ×1 |
= |
9 |
» 0, 391. ♦ |
|
|
||||
|
0, 46 |
|
23 |
||
ФОРМУЛА БЕРНУЛЛИ ЛОКАЛЬНАЯ ТЕОРЕМА МУАВРА-ЛАПЛАСА
ИНТЕГРАЛЬНАЯ ТЕОРЕМА МУАВРА-ЛАПЛАСА ФОРМУЛА ПУАССОНА
Повторение испытания – это последовательное проведение n раз одного и того же опыта или одновременное проведение n одинаковых опытов.
Испытаниями Бернулли называют последовательность испытаний, удовлетворяющую следующим условиям:
1) при каждом испытании различают лишь два исхода – появление некоторого события А либо не появление события А (событие А );
2) испытания являются независимыми, т.е. вероятность успеха в k-м испытании не зависит от исходов всех испытаний до k-го;

27
3) вероятность появления события А во всех испытаниях постоянна и равна P ( A) = p .Вероятность появления события А
в каждом испытании обозначим q, т. е. P( A) = 1 - p = q .
Постановка задачи. Пусть производится n независимых испытаний Бернулли. Необходимо найти вероятность того, что событие А появится ровно k раз.
Вероятность Pn (k ) того, что в n независимых испытаниях
Бернулли событие А появится ровно k раз, определяется
формулой Бернулли
Pn (k) = Cnk × pk × qn−k |
(18) |
П р и м е р 27. Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти вероятность появления 3 стандартных деталей среди 5 отобранных.
Р е ш е н и е.
Вероятность изготовления стандартной детали p=0,8, тогда q=1–0,8=0,2; n=5, k=3. Искомую вероятность находим по формуле (18):
P5 (3) = C53 ×0,83 ×0, 22 = 5 × 4 ×3 × 0,83 ×0, 22 = 0, 2048 .♦ 3!
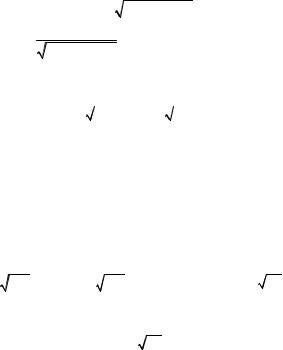
Если в испытаниях Бернулли число испытаний n «велико», причем «велики» также вероятности p и q, то для всех k справедлива локальная теорема Муавра-Лапласа:
|
|
|
|
|
|
|
|
|
|
|
Pn (k) » |
1 |
|
×ϕ ( x) , |
(19) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
npq |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где x = |
k |
- np |
|
|
ϕ ( x) = |
1 |
|
|
×e− |
x2 |
|
|
|
|
|
|
|||||||
|
, |
|
|
2 |
. |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
npq |
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
||||||
Имеются |
|
таблицы, |
в |
|
которых определены значения |
||||||||||||||||||
функции ϕ ( x) |
= |
|
1 |
|
×e− |
x2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
, |
соответствующие |
неотрицательным |
||||||||||||||||||
|
|
|
|||||||||||||||||||||
2π |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
значениям x . Для отрицательных значений x |
используют те же |
||||||||||||||||||||||
28
таблицы, так как функция ϕ ( x) четная, т.е. ϕ (-x) = ϕ ( x) . Если x > 4 , то принято считать, что ϕ ( x) = 0 .
П р и м е р 28. Известно, что в среднем 60% всего числа изготовляемых заводом телефонных аппаратов является продукцией первого сорта. Чему равна вероятность того, что в изготовленной партии окажется 120 аппаратов первого сорта, если партия содержит 200 аппаратов?
Р е ш е н и е.
Вероятность того, что аппарат первого сорта равна p=0,6, тогда q=1–0,6=0,4. Так как n=200 и k=120 достаточно «велики» (npq=200×0,6×0,4=48>9), то применяем локальную теорему Муавра-Лапласа (19):
P200 |
(120) » |
|
|
1 |
|
|
×ϕ ( x) ; |
|
|
|
|
|
|||
|
× 0, 6 |
× 0, 4 |
|||||
|
200 |
|
|
||||
= 120 - 200 × 0, 6 =
Определим x 0 .
200 ×0, 6 ×0, 4
По таблице (приложение 2) найдем ϕ (0) = 0, 3989 , тогда
P200 |
(120) » |
|
1 |
|
×ϕ (0) = |
0, |
3989 |
= 0, 0576 .¨ |
|
|
|
|
|
|
|
||||
|
|
|
|||||||
|
48 |
48 |
|
|
|||||
Если в испытаниях Бернулли число испытаний n «велико», причем «велики» также вероятности p и q, то для вероятности того, что число k появлений события А заключено в пределах от k1 до k2 (включительно), справедлива интегральная теорема Муавра-Лапласа:
|
|
|
|
|
Pn {k1 £ k £ k2 } = F ( x2 ) - F ( x1 ) , |
|
|
(20) |
|||||||||||||||
|
|
- np |
|
|
|
|
|
- np |
|
|
|
|
|
|
x |
|
|
|
|
x |
y2 |
||
где x1 = |
k1 |
|
, |
x2 |
= |
k2 |
, |
F ( x) = ∫ϕ |
( y) dy = |
|
1 |
|
∫ e− |
|
dy - |
||||||||
|
|
|
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
npq |
2π |
||||||||||||||||||
|
|
npq |
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|||||||||
интеграл Лапласа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y2 |
|
|
|
|
|
|
|
|
Для интеграла |
|
F ( x) = |
|
1 |
|
∫ e− |
|
|
имеются |
|
таблицы |
||||||||||||
|
|
|
2 dy |
|
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
2π |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
значений, соответствующие положительным значениям x и для x = 0 . Для x < 0 используют те же таблицы, учитывая, что

29
функция F ( x) нечетная, т. е. F (-x) = -F ( x) . В таблицах
приведены значения интеграла лишь до x = 5 , так как для x > 5 можно принять F ( x) = 0,5 .
П р и м е р 29. Найти вероятность того, что при 600 бросаниях игральной кости выпадет от 90 до 120 «шестерок».
Р е ш е н и е.
Вероятность выпадения «шестерки» при одном бросании игральной кости p=1/6, тогда q=1–1/6=5/6, n=600, k1=90 и k2=120
(npq=600×1/6×5/6»83,3>9).
Воспользуемся интегральной теоремой Лапласа (20). Вычислим
x1 |
и x2 |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
= |
k1 |
- np |
|
= |
90 - 600 × 16 |
|
» -1, 09, x2 |
= |
k2 |
- np |
= |
120 - 600 |
× 16 |
|
» 2,19. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
600 × 1 |
× 5 |
|
|
|
|
× 5 |
|||||||||||||
|
|
|
npq |
|
|
|
|
npq |
600 × 1 |
|
|
|||||||||
|
|
|
|
|
|
6 |
6 |
|
|
|
|
|
6 |
6 |
|
|
||||
Учитывая, что функция Лапласа нечетна, т.е. F (-x) = -F ( x) ,
получим
P600 {90 £ k £ 120} = F (2,19) - F (-1, 09) = F (2,19) + F (1, 09) .
По таблице (приложение 1) найдем
F (2,19) =0,48575, F (1, 09) =0,3621.
Искомая вероятность
P600 {90 £ k £ 120} = 0, 48575 + 0,3621 = 0,84785. ¨
Пусть число испытаний Бернулли n «велико», а вероятность p в одном испытании «мала», причем достаточно
«мало» также произведение λ = np . Тогда Pn (k ) |
определяют по |
||
формуле Пуассона: |
(k) » λ k |
|
|
Pn |
× e−λ |
(21) |
|
|
k ! |
|
|
П р и м е р 30. Завод отправил на базу 10 000 стандартных изделий. Среднее число изделий повреждаемых при транспортировке, составляет 0,02%. Найти вероятность того, что из 10 000 изделий будет повреждено 3.
Р е ш е н и е.

30
Вероятность того, что изделие будет повреждено при транспортировке, равна p=0,0002. Так как p – мала, n=10 000 –
велико и λ = np = 10 000 ×0, 0002 = 2 £ 9 , |
то следует применить |
|||
формулу Пуассона (21): P10 000 |
(3) » |
23 |
×e−2 |
= 0,1804 . |
|
||||
|
3! |
|
|
|
e−2 = 0,13534 (приложение 3).♦
ОТКЛОНЕНИЕ ОТНОСИТЕЛЬНОЙ ЧАСТОТЫ ОТ ПОСТОЯННОЙ ВЕРОЯТНОСТИ В НЕЗАВИСИМЫХ ИСПЫТАНИЯХ
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p, абсолютная величина отклонения относительной частоты появления события от вероятности появления события не превысит положительного числа ε , приближенно равна
удвоенной функции Лапласа при x = ε × 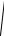
|
|
m |
|
|
|
|
|
|
|
|
|
||||||
P |
|
|
|
- p |
|
£ ε |
= 2F |
ε × |
|
||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
||||||
n : pq
n |
|
|
(22) |
|
|
|
|
|
|||
|
|
|
|
pq |
|
||
П р и м е р 31. Вероятность появления события в каждом из 900 независимых испытаний равна 0,5.Найти вероятность того, что относительная частота появления события отклоняется от вероятности по абсолютной величине не более чем на 0,02.
Р е ш е н и е.
По условию задачи n = 900; |
p = 0, 5; |
q = 0, 5; |
|
ε = 0, 02. |
||||||||||||||||||||||
Необходимо найти P |
|
|
m |
- 0, 5 |
|
£ 0, 02 . |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
По формуле (22) имеем |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
900 |
|
= 2F (1, 2). |
||||||||
P |
|
|
|
|
|
|
|
- 0, 5 |
£ |
0, 02 |
= |
2F 0, 02 |
× |
|
|
|
|
|||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, 5 ×0,5 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
По таблице (приложение 1) находим F (1, 2) = 0, 3849 . Тогда |
||||||||||||||||||||||||||
|
|
m |
- 0, 5 |
|
£ |
|
|
|
|
|
= 2F (1, 2) = 2 ×0,3849 |
= 0, 7698. ♦ |
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
P |
|
|
|
|
0, 02 |
|||||||||||||||||||||
|
||||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
