Решение

По закону Ома для замкнутой цепи (1), где е - электродвижущая сила источника тока,r - его внутреннее сопротивления, R- сопротивление внешней цепи.

Напряжения на резисторе найдем из закона Ома для однородного участка цепи: , т.е (2)

Коэффициент полезного действия – это отношение полезной мощности к затраченной мощности, т. е(3)

Вычислим искомые величины по формулам (1) , (2) , (3):

, , .

Ответ: ; ; .

Пример №5. Плотность электрического тока в медном проводнике . Найти объемную плотность тепловой мощности тока в этом проводнике. Удельное сопротивление меди.

Дано: ω- ?

Решение: Согласно закона Джоуля-Ленца в дифференциальной форме объемная плотность тепловой мощности или(1),

где – удельная электропроводность, с – удельное сопротивление проводника, Е – напряженность электрического поля в проводнике.

Согласно закону Ома в дифференциальной форме плотность тока в проводнике равна:

. (2)

Из формулы (2) найдем и, подставив в формулу (1), получим.

Проверим справедливость формулы по размерности величин:

.

Вычислим искомую величину:

.

Ответ: .

Пример №6. Под каким напряжением нужно передавать электроэнергию на расстояние 10км, чтобы при плотности тока в стальных проводах двухпроводной линии потери в линии составляли 1% передаваемой мощности? Удельное сопротивление стали .

Дано:

U – ?

Решение

Передаваемая мощность к потребителю равна (1), где, (2) сила тока в линии передач, - плотность тока в проводе сечения .

При прохождения тока по проводнику он нагревается. Это определит потери мощности, которые можно найти из закона Джоуля-Ленца.

Потеря мощности равна (3), гдеR - сопротивление двухпроводной линии (4).

В формуле (4): l – расстояние до потребителя электроэнергии.

Потеря мощности определяется по формуле или, используя формулы (1) и (3), получим.

Отсюда напряжение .

Используя формулы (2) и (4) получим .

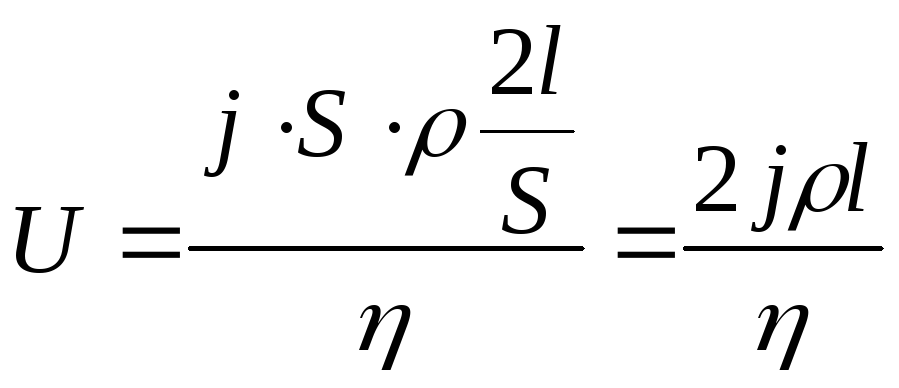Проверим справедливость формулы по размерности величин:

.

Вычислим значение искомого напряжения:

.

Ответ: .

Пример №7. Два параллельных бесконечно длинных провода А и С, по которым текут в одном направлении токи силой I₁ = I₂ = I = 50 А, расположены на расстоянии d = 10 см друг от друга. Определить магнитную индукцию поля, создаваемого проводниками с током в точкеD, отстоящей от оси одного провода на расстоянии r₁ = 5 см, от другого – на r₂= 12 см.

Дано:	Решение:
I1 = I2 = I = = 50 А d = 10 см = = 0,10 м r1 = 5 см = = 0,05 м r2 = 12 см = = 0,12 м	Воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитных индукций иполей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически:. Модуль вектора В может быть найден по теореме косинусов: , гдеα – угол между векторами и.
-?

; .

Тогда

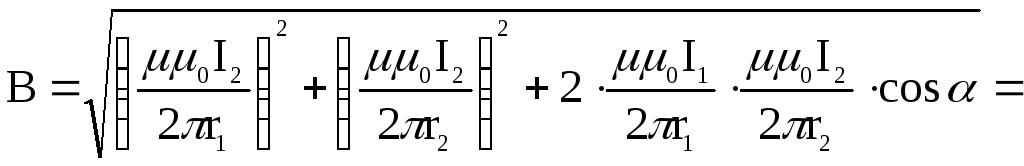
. (1)

Угол α =ADC – как углы при вершинах треугольников с взаимно перпендикулярными сторонами.

Из АDС по теореме косинусов запишем:

, откуда .

Подставим числовые значения и произведем вычисления:

.

Подставив в формулу (1) числовые значения физических величин, получим:

Ответ: В = 357,1 мкТл.

Пример №8. По тонкому стержню длиной l = 50 см равномерно распределен заряд q = 60 нКл. Стержень вращается с частотой ν = 12 с^–1 относительно оси, перпендикулярной стержню и проходящей через стержень на расстоянии а =l от одного из его концов. Определить магнитный момент P_m, обусловленный вращением стержня.

Дано:	Решение:
l =50 см = 0,50 м q = 60 нКл = 6010-9 Кл ν= 12 с–1 а =l	По определению магнитный момент плоского контура с током I равен: , где – единичный вектор нормали к плоскости контураS. Выделим элемент стержня длиной dr с зарядом на нем . При вращении стержня относительно осиО элементарный круговой ток в данном случае определяется выражением
Pm -?

=νdq,

где  - частота вращения стержня. Магнитный момент элементарного кругового тока dP_m = SdI, где S – площадь, ограниченная окружностью, описываемой элементом стержня dr с зарядом dq (S = r², где r – радиус этой окружности).

Т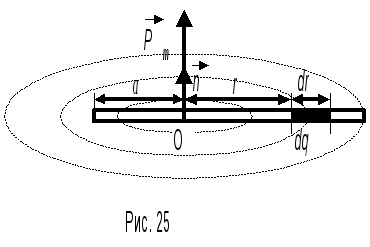огда.

Магнитный момент P_m, обусловленный вращением стержня длиной l вокруг оси О, определяем интегрированием двух частей стержня: ,

где 0, и– пределы интегрирования.

.

.

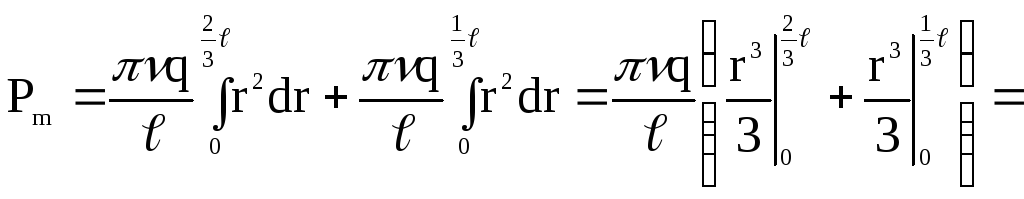
Произведем вычисления:

.

Ответ: P_m = 62,8 нАм².

Пример №9. Электрон движется в однородном магнитном поле (В=10 мТл) по винтовой линии, радиус которой R = 1 см и шаг h = 6 см. Определить период Т обращения электрона и его скорость .

Дано:	Решение:
В = 10 мТл = 1010-3 Тл R = 1 см = 10-2 м h = 6 см = 610-2 м	Электрон будет двигаться по винтовой линии, если он влетает в однородное магнитное поле под некоторым углом () к линиям магнитной индукции. Разложим, как показано на рисунке, скоростьэлектрона на две составляющие:
Т-? -?

.

По модулю , где;.

На электрон действует сила Лоренца

Рисунок33

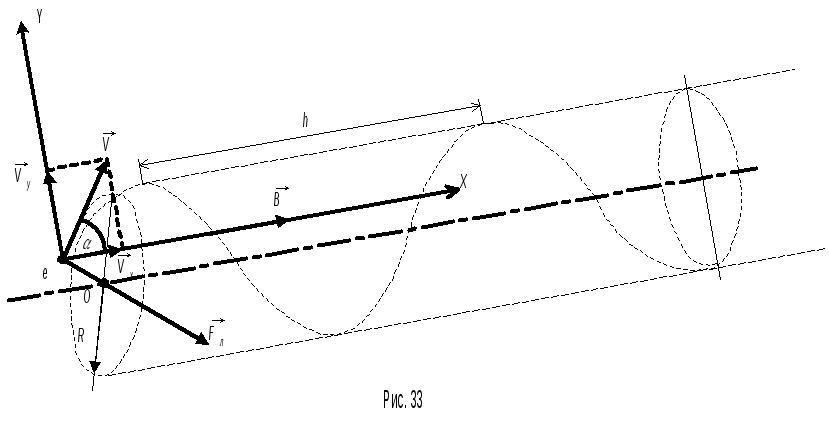
Сила Лоренца сообщает электрону нормальное ускорение . Согласно второму закону Ньютона можно написать, или, откуда. Период обращения электрона связан с составляющей скоростисоотношением:. Тогда получим:.

Произведем вычисления:

.

За время, равное периоду обращения Т, электрон пройдет вдоль силовой линии расстояние, равное шагу винтовой линии, т.е. , откуда

.

Модуль скорости электрона

.

П

Рис. 44

Рисунок 44

одставим числовые значения величин и произведем вычисления:

Ответ: Т = 3,57 нс, = 24,6 Мм/с.

Пример № 10. Катушка, содержащая N = 1000 витков, равномерно вращается с частотой  = 10 с^-1 относительно оси АВ, лежащей в плоскости катушки и перпендикулярной линиям индукции однородного магнитного поля (В = 0,04 Тл). Определить мгновенное значение ЭДС индукции для тех моментов времени, когда плоскость катушки составляет угол α = 60 с линиями поля. Площадь катушки S = 100 см².

Дано:	Решение:
N = 1000  = 10 с-1 В = 0,04 Тл α = 60 S = 100 см2 = 10-2 м2	По закону Фарадея-Ленца: . Потокосцепление , гдеN – число витков катушки, пронизываемых магнитным потоком Ф. Тогда получим: . Магнитный поток, пронизывающий катушку в момент времениt, определяется по закону , где ω – угловая скорость вращения катушки ().
i-?

Мгновенное значение ЭДС индукции:. Если учесть, что угол(рисунок), а, то получим:. Проведем вычисления:

Ответ: ε_i =12,56 В.