
- •Учебное пособие
- •Содержание
- •1. Электричество и магнетизм
- •1.1. Основные формулы по электричеству и магнетизму
- •1.2. Примеры решения задач к разделу «Электричество и магнетизм»
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •1.3. Базовые задачи для самостоятельного решения
- •1.4. Контрольные вопросы
- •2. Оптика
- •2.1. Основные формулы
- •2.2. Примеры решения задач к разделу «Оптика»
- •2.3. Базовые задачи для самостоятельного решения
- •2.4. Контрольные вопросы
- •3. Квантовая физика
- •3.1. Основные понятия и формулы к разделу «Квантовая физика »
- •3.2. Примеры решения задач к разделу «Физика атома и атомного ядра»
- •Решение
- •3.3. Базовые задачи для самостоятельного решения
- •3.4. Контрольные вопросы
- •Библиографический список
- •Приложения
- •1. Основные физические постоянные
- •2. Диэлектрическая проницаемость
- •3. Удельное сопротивление металлов
- •4. Показатель преломления
- •5. Массы некоторых изотопов, а.Е.М.
- •6. Периоды полураспада некоторых радиоактивных элементов
3.2. Примеры решения задач к разделу «Физика атома и атомного ядра»
Пример №1. Найти: а) радиус первой боровськой орбиты для однократно ионизированного гелия; б) скорость электрона на ней.
Решение
Электрон в водородоподобном атоме двигается по круговой орбите, поэтому кулоновская сила взаимодействия электрона и ядра является центростремительной силой, то есть
![]() ,
,
где z – номер
элемента, е – заряд электрона,
![]() Кл, r – радиус орбиты,
– скорость электрона на орбите, 0
– электрическая
постоянная, m – масса электрона,
m=9,110-31
кг.
Кл, r – радиус орбиты,
– скорость электрона на орбите, 0
– электрическая
постоянная, m – масса электрона,
m=9,110-31
кг.
По
второму постулату Бора момент импульса
электрона на любой орбите удовлетворяет
условие:
![]() ,
,
где n – номер орбиты, h – стала Планка, h=6.6310-34 Дж·с, r, – соответственно радиус орбиты и скорость электрона на ней.
Решим систему уравнений:
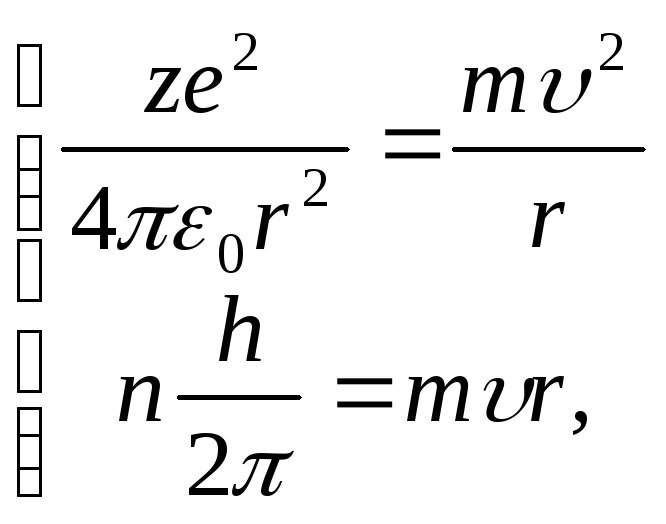
разделим первое уравнение на второе и получим:
![]() или
или
![]() ,
,
по условию задачи z=2, n=1.
Соответственно:
=
![]()
![]() =
=![]() ,
,
рассчитаем:
![]() .
.
По второму постулату Бора определим радиус орбиты:
![]() .
.
Соответственно:
![]() ,
если n=1,
то
,
если n=1,
то
![]() ,
,
рассчитаем:
![]() (м).
(м).
Ответ:![]() ,
,
![]() м.
м.
Пример
№2.
Определить,
какое количество ядер радиоактивного
препарата
![]() ,
взятого в количестве 0,2мг, распадается
в течение: а) 2с; б) 1ч.
,
взятого в количестве 0,2мг, распадается
в течение: а) 2с; б) 1ч.
Дано:
|
|
Решение:
Число нераспавшихся
радиоактивных ядер
|
|
|
Тогда
число распавшихся ядер за время
|
Постоянная
радиоактивного распада связана с
периодом полураспада Т соотношением:
![]() .
Число радиоактивных ядер в данной массе
вещества вычисляется с помощью закона
Авогадро:
.
Число радиоактивных ядер в данной массе
вещества вычисляется с помощью закона
Авогадро:![]() ,
(3)
,
(3)
где
![]() - масса одного моля;
- масса одного моля;![]() -масса вещества;
-масса вещества;![]() - число Авогадро.
- число Авогадро.
С учетом значения
![]() и
и![]() формула (2) примет вид:
формула (2) примет вид:![]() (4).
(4).
Если время распада
t значительно меньше периода полураспада
Т(t<<T), получим:
![]() (5). Число распавшихся за время распада
(5). Число распавшихся за время распада![]() ядер вычисляется по формуле (5). Подставим
числовые данные и определим
ядер вычисляется по формуле (5). Подставим
числовые данные и определим![]() .
Для второго промежутка времени
.
Для второго промежутка времени![]() нельзя применить приближенную формулу
(5), так как
нельзя применить приближенную формулу
(5), так как![]() ,
поэтому вычисление распавшегося числа
атомов произведем по формуле (4):
,
поэтому вычисление распавшегося числа
атомов произведем по формуле (4):
![]()
Ответ:![]()
Пример
№3.
Вычислить дефект массы и энергию связи
ядра
![]() .
.
Дано:
|
|
Решение: Масса ядра всегда меньше суммы масс свободных протонов и нейтронов, из которых состоят ядра. |
|
|
Дефект
массы ядра
|
где
![]() - порядковый номер элемента (число
протонов в ядре); А – массовое число
(число нуклонов в ядре);
- порядковый номер элемента (число
протонов в ядре); А – массовое число
(число нуклонов в ядре);![]() – соответственно масса протона, нейтрона
и ядра. Так как в справочных таблицах
приводятся массы нейтральных атомов,
а не ядер, то дефект массы вычислим по
формуле:
– соответственно масса протона, нейтрона
и ядра. Так как в справочных таблицах
приводятся массы нейтральных атомов,
а не ядер, то дефект массы вычислим по
формуле:
![]() .
(2)
.
(2)
Так как ![]() =
=
![]() ,
где m
,
где m![]() - масса изотопа водорода
- масса изотопа водорода
![]() ,
то формула (2) примет вид:
,
то формула (2) примет вид:
![]() (3)
(3)
Подставим в выражение (3) числовые данные и вычислим
![]()
В соответствии с законом взаимосвязи массы и энергии, Дж
![]() ,
(4)
,
(4)
где ![]() - энергия связи, численно равная работе,
которую необходимо затратить, чтобы
разделить ядро на отдельные, не
взаимодействующие между собой частицы
без сообщения им кинетической энергии;
- энергия связи, численно равная работе,
которую необходимо затратить, чтобы
разделить ядро на отдельные, не
взаимодействующие между собой частицы
без сообщения им кинетической энергии;
![]() - дефект массы ядра; с – скорость света
в вакууме.
- дефект массы ядра; с – скорость света
в вакууме.
Так как дефект массы выражен во внесистемных единицах (а.е.м.), то энергия связи ядра: МэВ (5)
Подставим
в формулу (5) числовое значение дефекта
массы и вычислим
![]() (МэВ).
(МэВ).
Ответ:
![]() МэВ
МэВ
Пример
№4.
Найти удельную энергию связи нуклонов
в ядрах
![]() и
и![]() .
Ядро какого элемента наиболее устойчиво?
.
Ядро какого элемента наиболее устойчиво?
Дано:
|
|
Решение:
Удельная энергия
связи нуклонов в ядре – это энергия
связи, приходящаяся на один нуклон.
Удельная энергия связи может быть
вычислена по формуле
|
|
|
где
|
Если дефект массы выразить в атомных единицах массы, то энергия связи нуклонов в ядре может быть вычислена по формуле, МэВ
МэВ. (2)
Дефект массы ядра
определяется разностью масс свободных
нуклонов и массой ядра:
(3), где Z
– число протонов в ядре – порядковый
номер элемента; (А-Z)
– число нейтронов в ядре;
![]() – соответственная масса протона,
нейтрона и ядра элемента. В справочных
таблицах приводятся массы не ядер, а
нейтральных атомов, поэтому преобразуем
формулу (3) так, чтобы пользоваться массой
нейтрального атома
– соответственная масса протона,
нейтрона и ядра элемента. В справочных
таблицах приводятся массы не ядер, а
нейтральных атомов, поэтому преобразуем
формулу (3) так, чтобы пользоваться массой
нейтрального атома
![]() (4), где
(4), где
![]() - масса изотопа атома водорода.
- масса изотопа атома водорода.
Подставим формулу
(4) в (2) и полученное выражение
![]() в формулу (1), получим формулу для расчета
удельной энергии связи
в формулу (1), получим формулу для расчета
удельной энергии связи
![]() .
(5)
.
(5)
Подставим числовые данные и вычислим удельную энергию связи:

Так как удельная энергия связи нуклонов в ядре кобальта больше удельной энергии связи ядра урана, то более устойчиво ядро кобальта.
Ответ:
![]() Устойчивее ядро кобальта.
Устойчивее ядро кобальта.
Пример №5 . Вычислить в мегаэлектроновольтах энергию ядерной реакции
![]() .
Выделяется или поглощается энергия при
этой реакции?
.
Выделяется или поглощается энергия при
этой реакции?
Дано:
|
|
Решение: Чтобы
вычислить энергию ядерной реакции
|
|
|
|
![]() Дефект
массы:
Дефект
массы:
![]() .
(2)
.
(2)
Так как число электронов до и после реакции сохраняется, вместо значений масс ядер воспользуемся значениями масс нейтральных атомов:
![]()
Реакция
протекает с выделением энергии, так как
![]() >0.
Подставив значение
>0.
Подставив значение![]() в
(1), получим
в
(1), получим
![]() .
Реакция экзотермическая.
.
Реакция экзотермическая.
Ответ:
![]() .
Реакция экзотермическая.
.
Реакция экзотермическая.





