2.2.3. Фактичний стан дороги

Фактичний стан ділянки дороги оцінюється шляхом аналізу лінійного експлуатаційного графіка (див. рис. 2), в якому вказуються основні техніко-експлуатаційні та геометричні параметри дороги.

Бічна ситуація
Кілометри	0	1	2	3	4	5	6	7	8	9
Категорія
Ширина проїзної частини
Кількість смуг руху
Ширина смуг руху
Ширина узбіччя (ліве/праве)
Тип укріплення узбіччя
Конструкція дорожнього одягу
Ґрунт земляного полотна
Дислокація штучних споруд
Коефіцієнт зчеплення
Рівність покриття
Поздовжні похили, о/оо
Радіуси кривих, м

Рис. 2. Лінійний експлуатаційний графік дороги

2.3. Аналіз даних про рух і прогноз вантажного режиму

Аналіз даних про рух і прогноз вантажного режиму на дорозі здійснюється на основі статистичних даних обліку руху для даної ділянки дороги за попередній період часу (від 8 до 15 років). Завдяки цьому встановлюють закон зміни інтенсивності й складу руху, а потім екстраполюють на досліджуваний період часу (5-10 років).

Статистичний прогноз інтенсивності руху починають зі складання вихідних даних за формою таблиці 2.1.

Таблиця 2.1

Показник	Рік
	2001	2002	2003	2004	2005	2006	2007	2008	2009	2010
	Порядковий номер року
	0	1	2	3	4	5	6	7	8	9
Середньодобова інтенсивність руху N, авт/добу
lg N(t)
	=					=
	=					=
	= 10					= 35

За даними статистичного ряду будують графік емпіричного зв'язку «роки t– інтенсивність рухуN» у вигляді ламаної лінії, яка з'єднує точки з координатами [t_i ; N_i ], і за характером цього зв'язку складають уявлення про можливу форму закону зміни інтенсивності руху на даній ділянці дороги з часом.

Найбільш часто шуканому емпіричному зв'язку «t − N» відповідає один із наведених виразів:

N(t) = N0 = const;	/2.3/
N(t) = N0 + a  t;	/2.4/
N(t) = N0 ( 1 + q ) t= N0 Q t;	/2.5/
N(t) = N0  e b t,	/2.6/

де N(t), N₀– інтенсивність руху відповідно вt-й та нульовий (приt = 0) роки;

а, b– коефіцієнти, що визначають темпи зростання інтенсивності руху;

q– щорічний приріст руху на дорозі (0,01  q  0,15).

Після вибору форми закону здійснюють математичне апроксимування емпіричного зв'язку вибраним законом, тобто встановлюють такі параметри вибраного закону, за яких він задовольняє даний емпіричний зв'язок.

Параметри, що підлягають установленню, у виразі /2.4/ є N₀таa, у /2.5/ −N₀іq, у /2.6/ −N₀іb.

Математичне апроксимування емпіричного зв'язку «t − N» уручну найліпше виконати методом середніх, який не потребує проведення громіздких розрахунків і в той самий час забезпечує достатню точність результатів. Визначення невідомих параметрів виразу зводиться до розв'язування системи лінійних рівнянь, кількість яких відповідає числу невідомих параметрів виразу.

При апроксимуванні емпіричного зв'язку «t − N» виразом вигляду /2.4/ з використанням методу середніх система рівнянь для визначення невідомих параметрівN₀ таaскладатиметься з двох рівнянь і матиме вигляд:

/2.7/

де n– кількість років статистичного ряду, що використані для побудови емпіричного зв'язку «t − N».

З розв'язку системи рівнянь /2.7/ одержують шукані числові параметри виразу /2.4/ − N₀таa.

При використанні методу середніх для нелінійних залежностей /2.5/ і /2.6/ спочатку проведемо їх анаморфозу − перетворення шляхом логарифмування до такого виразу, за якого між змінними досягається лінійний зв'язок.

Вираз /2.5/ після проведення анаморфозу шляхом його логарифмування матиме вигляд:

lg N (t) = lg N0 + t lg Q.

/2.8/

При апроксимуванні емпіричного зв'язку «t − N» виразом вигляду /2.8/ з використанням методу середніх система рівнянь для визначення невідомих параметрівN₀ таqскладатиметься з двох рівнянь і матиме вигляд:

/2.9/

а в результаті її розв'язання отримаємо значення lg N₀іlg Q, а відтак, і шукані параметри виразу /2.5/ −N₀іq.

Вираз /2.6/ після проведення анаморфозу шляхом його логарифмування матиме вигляд::

lg N (t) = lg N0 + b t lg e,

/2.10/

При апроксимуванні емпіричного зв'язку «t − N» виразом вигляду /2.10/ з використанням методу середніх система рівнянь для визначення невідомих параметрівN₀ таbскладатиметься з двох рівнянь і матиме вигляд:

/2.12/

а в результаті її розв'язання отримаємо значення lg N₀іlg Q, а відтак, і шукані параметри виразу /2.6/ −N₀іb.

Після встановлення числових параметрів за виразами /2.4 − 2.6/ переходять до їх аналізу з метою вибору найбільш оптимального вигляду емпіричного зв'язку «t − N», для чого розраховується квадратична похибка апроксимування за виразом

,

/2.13/

де N(t)_i– фактичні значення інтенсивності руху в кожнийі-й рік;

N_аі– апроксимовані значення інтенсивності руху ві-й рік.

Після встановлення теоретичного закону зміни інтенсивності руху в межах інтервалу років, що аналізується, приступають до складання прогнозу зміни інтенсивності руху на дорозі в межах прийнятого періоду планування (за межами інтервалу років, котрий аналізується), який приймається, як правило, 5-10 років.

Дану операцію виконують методом екстраполяції за встановленим теоретичним законом за межі досліджуваного періоду. Так для випадку, наведеного в таблиці 2.1, складання прогнозу інтенсивності руху починають із 2012 р., для якого приймаємо t = 10, на 2013 р. -t = 11 і т.д.

Якщо є відомості про зміну складу руху за ваговими групами транспортних засобів, то можливо виконати прогноз зміни складу руху «t–» (– частка кожної вагової групи у загальному потоці). Розрахунок виконується аналогічно наведеному розрахунку зміни інтенсивності руху.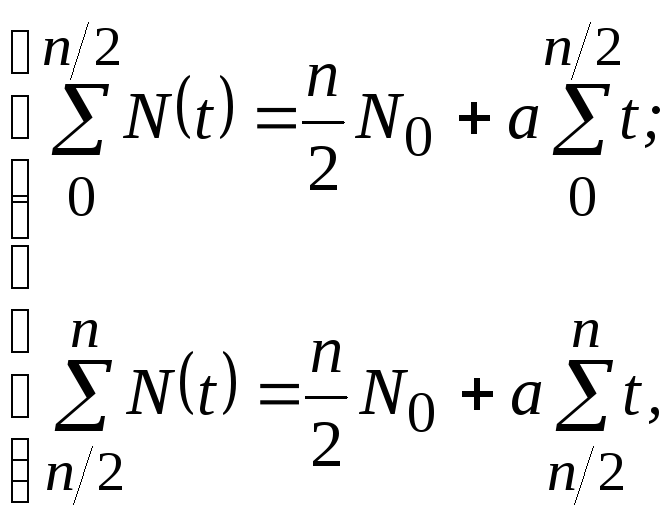
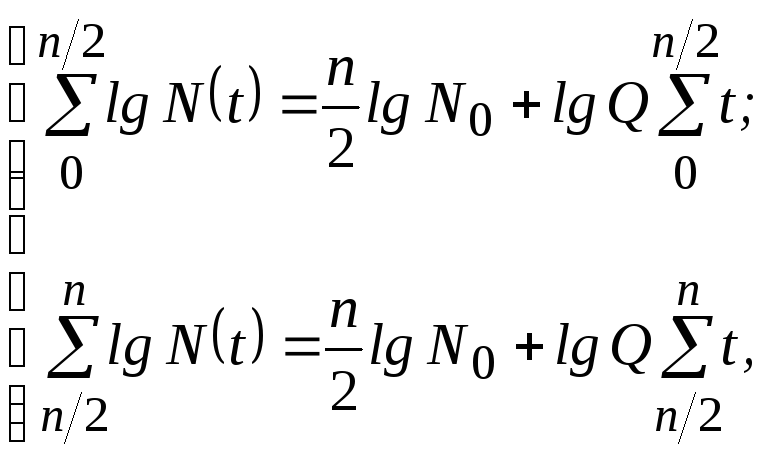
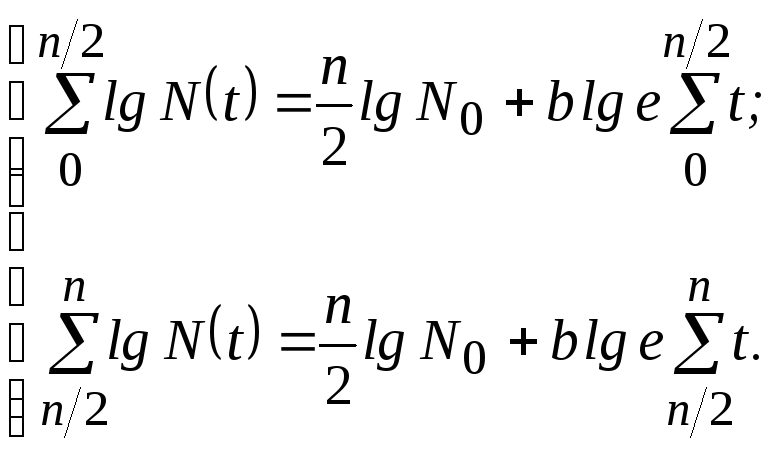
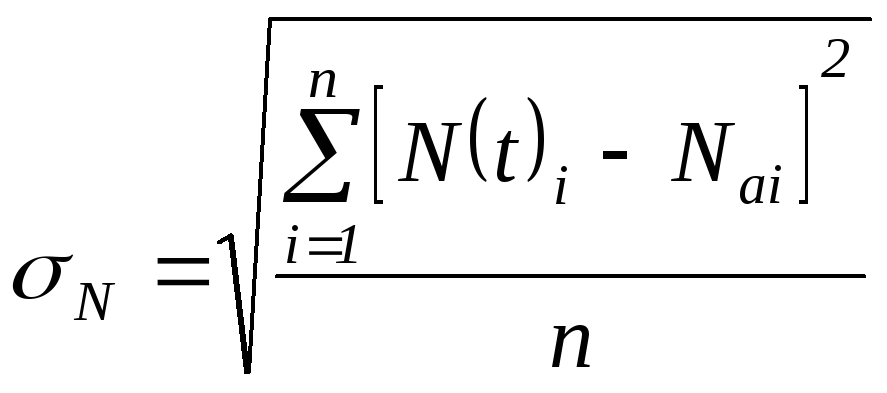