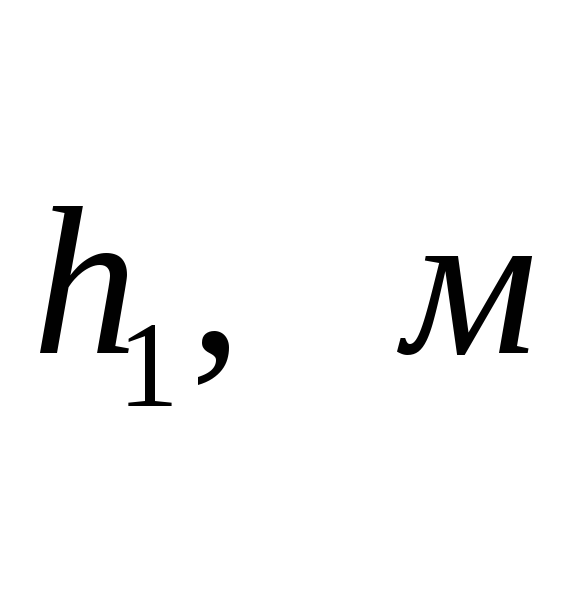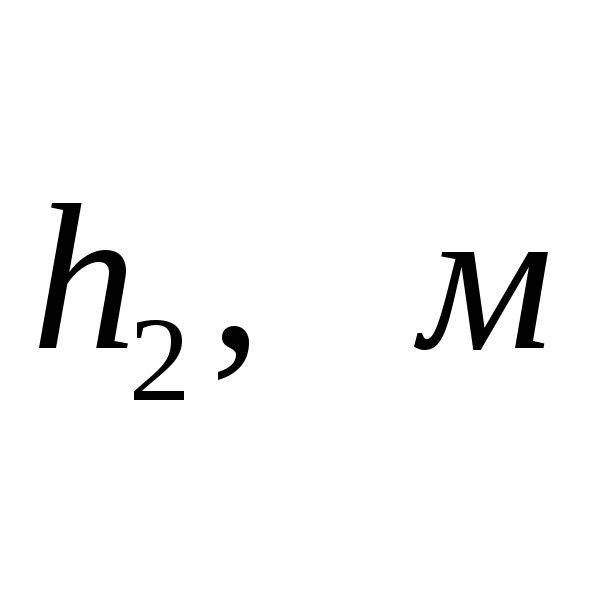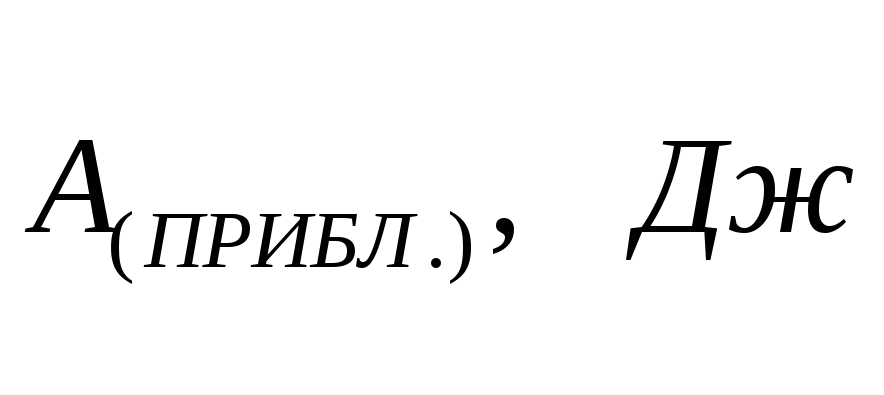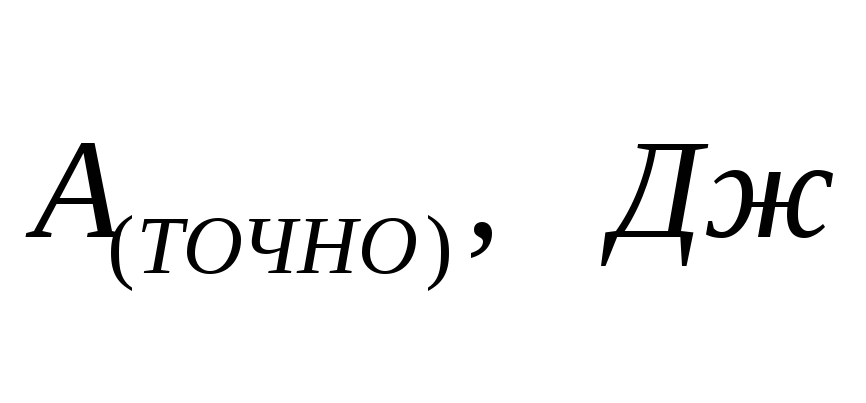- •Содержание Стр.
- •Введение
- •Техника безопасности Общие положения
- •Перед работой
- •Во время работы
- •После работы
- •Методические рекомендации к выполнению физического практикума
- •Содержание конспекта отчета по лабораторной работе
- •Вывод по лабораторной работе
- •Построение графиков
- •Оформление титульного листа
- •Расчет случайной ошибки
- •Лабораторная работа № 1 - 0
- •1.1. Случайные погрешности прямых измерений
- •В теории погрешностей в качестве единицы ширины доверительного интервала выбрана так называемая средняя квадратичная погрешность результата измерений:
- •1.2. Обработка результатов прямых измерений
- •1.3. Погрешность косвенных измерений
- •1.4. Обработка результатов косвенных измерений
- •1.5. Точность расчетов
- •1.6. Погрешности приборов
- •1.6. Некоторые измерительные инструменты и приборы Штангенциркуль
- •Пример:
- •Микрометр
- •Технические весы
- •При взвешивании необходимо выполнять следующие основные правила:
- •Порядок выполнения работы:
- •Контрольные вопросы:
- •Лабораторная работа № 1-1 Определение ускорения свободного падения
- •Краткая теория
- •Порядок выполнения работы, обработка результатов измерений:
- •Контрольные вопросы:
- •Краткая теория
- •Определение коэффициента вязкости жидкости по методу Стокса:
- •Описание установки
- •Порядок выполнения работы и обработка результатов измерений
- •Контрольные вопросы
- •Краткая теория
- •Описание установки, метод определения
- •Порядок выполнения работы
- •Лабораторная работа № 1-4 Определение момента инерции тел методом крутильных колебаний
- •Краткая теория
- •Указания по технике безопасности
- •Задание 1 Определение момента инерции тел правильной геометрической формы Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа № 1-5 Определение влажности воздуха с помощью психрометра Августа
- •Устройство психрометра и методика работы с ним
- •Порядок выполнения работы:
- •Контрольные вопросы
- •Лабораторная работа № 1-6 Определение коэффициента поверхностного натяжения жидкости методом отрыва пластины
- •Краткая теория
- •Описание установки и методика измерений
- •Порядок выполнения работы
- •Контрольные вопросы:
- •Краткая теория
- •Описание установки и методика измерений
- •Порядок выполнения работы:
- •Контрольные вопросы:
- •Лабораторная работа № 1 – 8 Изучение закона сохранения энергии на примере маятника Максвелла
- •Краткая теория
- •Порядок выполнения работы
- •Контрольные вопросы:
- •Приложения
Контрольные вопросы:
1. Дать определение коэффициента трения.
2. Определение коэффициента трения для горизонтальной и наклонной плоскости.
3. Причины возникновения трения.
4. Виды коэффициентов трения.
5. Объяснить полученные графики.
6. Как можно уменьшить силу трения.
7. Определение коэффициентов трения покоя и скольжения.
Пояснить баланс энергий формулы (3).
Лабораторная работа № 1 – 8 Изучение закона сохранения энергии на примере маятника Максвелла
Цель работы: изучить закон сохранения энергии
Оборудование:
1. Маятник Максвелла;
2. Линейка;
3. Секундомер;
4. Штангенциркуль.
Краткая теория
Маятник Максвелла представляет собой маховик с радиусом R на оси радиуса r (см. рис. 1).
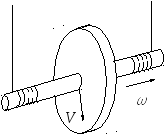
Рис.
1.
Схема
маятника Максвелла
На
эту ось с двух сторон наматываются нити,
в результате чего маховик поднимается
на высоту h.
При освобождении маховик движется вниз
и раскручивается под действием момента,
создаваемого силами натяжения нитей
![]()
Линейное
ускорение ![]() ,
направленное вниз, маятник приобретает
под действием разности сил натяжения
нитей и силы тяжести. Найдем это ускорение,
пренебрегая силами сопротивления. Из
следствия из второго закона Ньютона:
ma
= mg
– T;
согласно основному уравнению динамики
вращательного движения:
,
направленное вниз, маятник приобретает
под действием разности сил натяжения
нитей и силы тяжести. Найдем это ускорение,
пренебрегая силами сопротивления. Из
следствия из второго закона Ньютона:
ma
= mg
– T;
согласно основному уравнению динамики
вращательного движения: ![]() (*) . Учитывая, что момент инерции маховика:
(*) . Учитывая, что момент инерции маховика:
![]() ( моментом инерции оси можно пренебречь,
моментом инерции тела относительно оси
называется сумма произведений масс
всех материальных точек тела на квадраты
их расстояний до оси), и выразив угловое
ускорение через линейное:
( моментом инерции оси можно пренебречь,
моментом инерции тела относительно оси
называется сумма произведений масс
всех материальных точек тела на квадраты
их расстояний до оси), и выразив угловое
ускорение через линейное: ![]() ,
уравнение (*) можно представить в
скалярном виде:
,
уравнение (*) можно представить в
скалярном виде:
![]() ,
тогда решая полученную систему уравнений:
,
тогда решая полученную систему уравнений: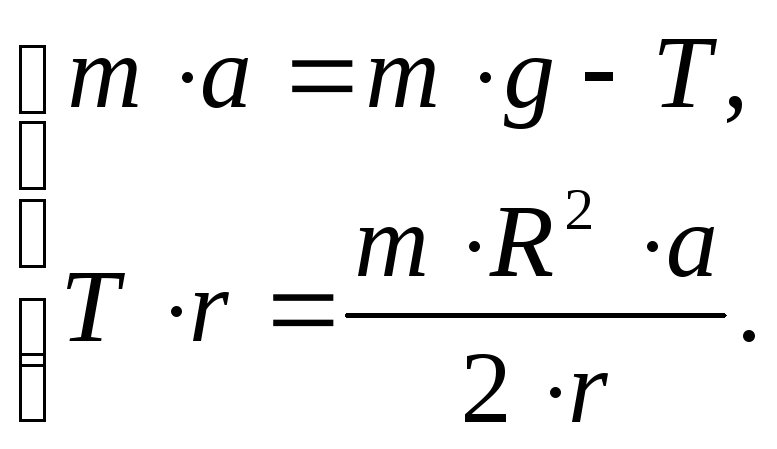
Можно
получить: ![]()
По
закону сохранения и превращения энергии
(в замкнутой системе энергия может
переходить из одних видов в другие и
предаваться от одного тела другому, но
ее общее количество остается неизменнной),
если маятник Максвелла спустится с
высоты h,
то часть его потенциальной энергии mgh
перейдет в кинетическую энергию
поступательного движения ![]() и кинетическую энергию
вращательного движения
и кинетическую энергию
вращательного движения ![]() ,
а часть пойдет на совершение работы А
против сил
сопротивления:
,
а часть пойдет на совершение работы А
против сил
сопротивления:
|
|
(1) |
Выразив угловую скорость маховика через линейную получим из (1):
|
|
(2) |
При равноускоренном движении без начальной скорости
Таким
образом, измерив время спуска маятника
Максвелла, можно найти его линейную
скорость в нижней точке υ
и, используя
(2), определить работу сил сопротивления.
Зная А,
![]() можно рассчитать
момент сил сопротивления (моментом сил
называется
можно рассчитать
момент сил сопротивления (моментом сил
называется  по формуле:
по формуле:
|
|
(3) |
Порядок выполнения работы
1. Штангенциркулем измерить диаметры маховика и оси, и найти их радиусы R и r соответственно.
2.
Закрутить маятник, подняв его на высоту
![]() относительно исходного положения при
этом сосчитать число оборотов маятника
N.
относительно исходного положения при
этом сосчитать число оборотов маятника
N.
Отпустить маятник и при помощи секундомера измерить время спуска до исходного положения t.
Измерить высоту вторичного подъема маятника
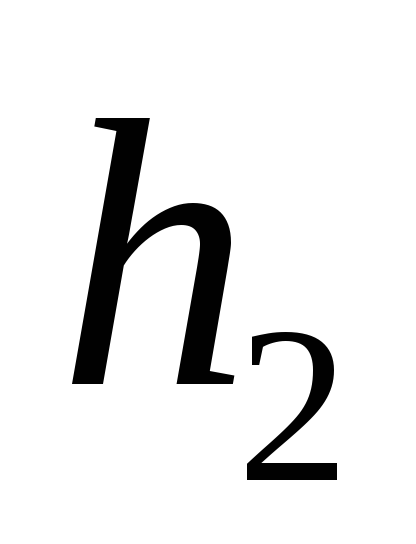 .
Полученные данные занести в таблицу.
.
Полученные данные занести в таблицу.Действия, описанные в пунктах 2 – 4 повторить 3 раза.
Рассчитать приближенное значение работы сил сопротивления по формуле
 и точное значение по формуле (2). Сравнить
полученные значения. По точному значению
А,
используя формулу (3), рассчитать момент
сил сопротивления. Результаты занести
в таблицу.
и точное значение по формуле (2). Сравнить
полученные значения. По точному значению
А,
используя формулу (3), рассчитать момент
сил сопротивления. Результаты занести
в таблицу.
7.
Рассчитать ![]() и
и ![]() .
Записать результат вычислений в виде:
.
Записать результат вычислений в виде:
![]() ,проделав необходимые
округления.
,проделав необходимые
округления.
8.
Для одного эксперимента рассчитать
фактическое линейное ускорение маятника
Максвелла по формуле ![]() и сравнить его с теоретическим значением
и сравнить его с теоретическим значением![]() Объяснить
расхождение.
Объяснить
расхождение.
Таблица
|
N |
|
|
t, c |
|
|
M, Н·м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|