
- •Содержание Стр.
- •Введение
- •Техника безопасности Общие положения
- •Перед работой
- •Во время работы
- •После работы
- •Методические рекомендации к выполнению физического практикума
- •Содержание конспекта отчета по лабораторной работе
- •Вывод по лабораторной работе
- •Построение графиков
- •Оформление титульного листа
- •Расчет случайной ошибки
- •Лабораторная работа № 1 - 0
- •1.1. Случайные погрешности прямых измерений
- •В теории погрешностей в качестве единицы ширины доверительного интервала выбрана так называемая средняя квадратичная погрешность результата измерений:
- •1.2. Обработка результатов прямых измерений
- •1.3. Погрешность косвенных измерений
- •1.4. Обработка результатов косвенных измерений
- •1.5. Точность расчетов
- •1.6. Погрешности приборов
- •1.6. Некоторые измерительные инструменты и приборы Штангенциркуль
- •Пример:
- •Микрометр
- •Технические весы
- •При взвешивании необходимо выполнять следующие основные правила:
- •Порядок выполнения работы:
- •Контрольные вопросы:
- •Лабораторная работа № 1-1 Определение ускорения свободного падения
- •Краткая теория
- •Порядок выполнения работы, обработка результатов измерений:
- •Контрольные вопросы:
- •Краткая теория
- •Определение коэффициента вязкости жидкости по методу Стокса:
- •Описание установки
- •Порядок выполнения работы и обработка результатов измерений
- •Контрольные вопросы
- •Краткая теория
- •Описание установки, метод определения
- •Порядок выполнения работы
- •Лабораторная работа № 1-4 Определение момента инерции тел методом крутильных колебаний
- •Краткая теория
- •Указания по технике безопасности
- •Задание 1 Определение момента инерции тел правильной геометрической формы Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа № 1-5 Определение влажности воздуха с помощью психрометра Августа
- •Устройство психрометра и методика работы с ним
- •Порядок выполнения работы:
- •Контрольные вопросы
- •Лабораторная работа № 1-6 Определение коэффициента поверхностного натяжения жидкости методом отрыва пластины
- •Краткая теория
- •Описание установки и методика измерений
- •Порядок выполнения работы
- •Контрольные вопросы:
- •Краткая теория
- •Описание установки и методика измерений
- •Порядок выполнения работы:
- •Контрольные вопросы:
- •Лабораторная работа № 1 – 8 Изучение закона сохранения энергии на примере маятника Максвелла
- •Краткая теория
- •Порядок выполнения работы
- •Контрольные вопросы:
- •Приложения
Краткая теория
Вязкость жидкости – это свойство, характеризующее возникновение сил внутреннего трения при относительном скольжении слоев жидкости, движущихся с различными скоростями, причем сила направлена по касательной к поверхности соприкосновения слоев.
При движении жидкости между её слоями возникают силы внутреннего трения, действующие таким образом, чтобы уравнять скорости всех слоёв.
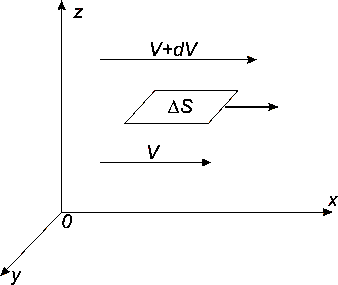
Рис. 1.
Движение жидкости
Природа этих сил заключается в том, что слои, движущиеся с разными скоростями, обмениваются молекулами, что приводит к перераспределению импульсов слоев жидкости. Молекулы из более быстрого слоя передают молекулам более медленного слоя часть импульса, вследствие чего медленный слой начинается двигаться быстрее, а быстрый слой тормозится.
Рассмотрим
жидкость, движущуюся в направлении х
(рис. 1). Пусть слои жидкости движутся с
разными скоростями. На оси
![]() возьмем две точки, находящиеся на
расстоянии
возьмем две точки, находящиеся на
расстоянии![]() .
Скорости потока жидкости отличаются в
этих точках на величину
.
Скорости потока жидкости отличаются в
этих точках на величину![]() .
Отношение
.
Отношение![]() характеризует изменение скорости потока
в направлении перпендикулярном
направлению скоростей и называетсяградиентом
скорости.
При ламинарном течении (т.е. без завихрений)
сила внутреннего
трения (или вязкости),
действующая между слоями, пропорциональна
площади их соприкосновения
характеризует изменение скорости потока
в направлении перпендикулярном
направлению скоростей и называетсяградиентом
скорости.
При ламинарном течении (т.е. без завихрений)
сила внутреннего
трения (или вязкости),
действующая между слоями, пропорциональна
площади их соприкосновения
![]() и градиенту скорости (формула Ньютона):
и градиенту скорости (формула Ньютона):
|
|
(15) |
Величина
![]() называетсякоэффициентом
внутреннего трения или коэффициентом
динамической вязкости. Величина
называетсякоэффициентом
внутреннего трения или коэффициентом
динамической вязкости. Величина
![]() называетсятекучестью.
Если в формуле (1) принять
называетсятекучестью.
Если в формуле (1) принять
![]() и
и
![]() ,
то
,
то
![]() ,
т.е.коэффициент
динамической вязкости численно равен
силе внутреннего трения, возникающей
на каждой единице поверхности
соприкосновения двух слоев, движущихся
один относительно другого с градиентом
скорости, равным единице. Наряду
с коэффициентом динамической вязкости
,
т.е.коэффициент
динамической вязкости численно равен
силе внутреннего трения, возникающей
на каждой единице поверхности
соприкосновения двух слоев, движущихся
один относительно другого с градиентом
скорости, равным единице. Наряду
с коэффициентом динамической вязкости
![]() ,
часто употребляют коэффициент
кинематической вязкости
,
часто употребляют коэффициент
кинематической вязкости![]() ,
где
,
где![]() – плотность жидкости. В системе СИ
единицей физических величин измерений
динамической вязкости
– плотность жидкости. В системе СИ
единицей физических величин измерений
динамической вязкости![]() ;
кинематической вязкости
;
кинематической вязкости![]() .
.
Коэффициент
динамической вязкости
![]() зависит от природы жидкости и для данной
жидкости с повышением температуры
уменьшается. Слой жидкости, непосредственно
прилегающий к твердой поверхности, в
результате прилипания остается
неподвижным относительно её. Скорость
остальных слоев постепенно возрастает
по мере удаления от твердой поверхности.
зависит от природы жидкости и для данной
жидкости с повышением температуры
уменьшается. Слой жидкости, непосредственно
прилегающий к твердой поверхности, в
результате прилипания остается
неподвижным относительно её. Скорость
остальных слоев постепенно возрастает
по мере удаления от твердой поверхности.
Определение коэффициента вязкости жидкости по методу Стокса:
На
всякое тело, движущееся в вязкой жидкости,
действует сила сопротивления. В общем
случае величина этой силы зависит от
многих факторов: от внутреннего трения
жидкости, от формы тела, от характера
обтекания и т.д. Стоксом было получено
строгое решение задачи о ламинарном
обтекании шарика безграничной жидкостью.
В этом случае сила сопротивления
![]() определяется формулой:
определяется формулой:
|
|
(2) |
где
![]() - скорость шарика,
- скорость шарика,![]() - радиус шарика,
- радиус шарика,![]() - коэффициент динамической вязкости
жидкости.
- коэффициент динамической вязкости
жидкости.
Рассмотрим падение шарика в вязкой среде (рис. 1). На шарик действуют три силы:
сила тяжести
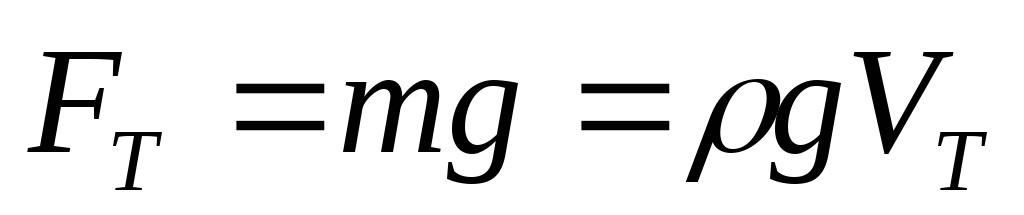 (ρ –
плотность материала шарика,
(ρ –
плотность материала шарика,
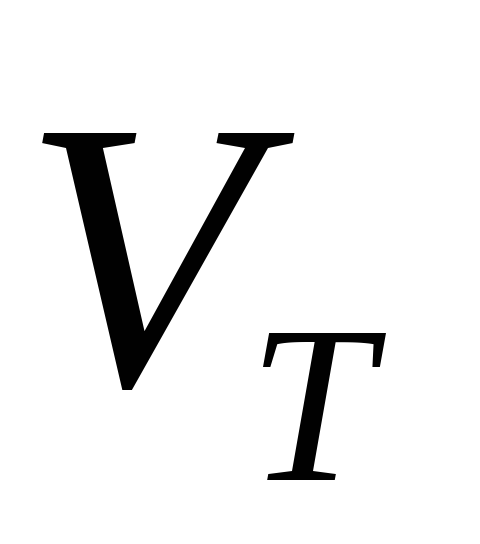
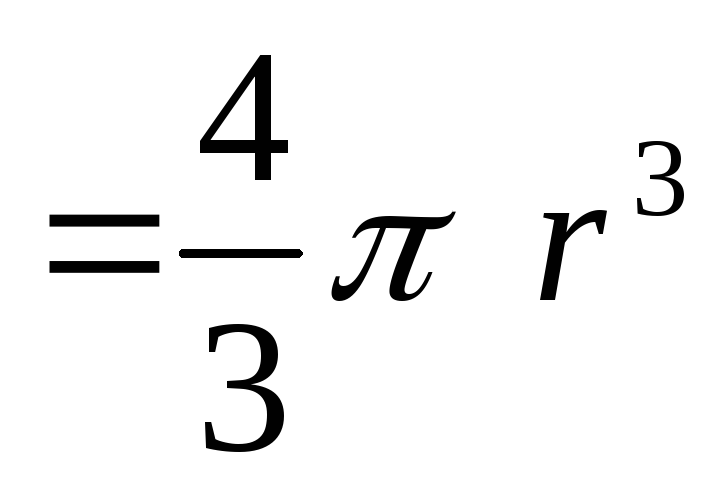 –
объем шарика);
–
объем шарика);сила Архимеда
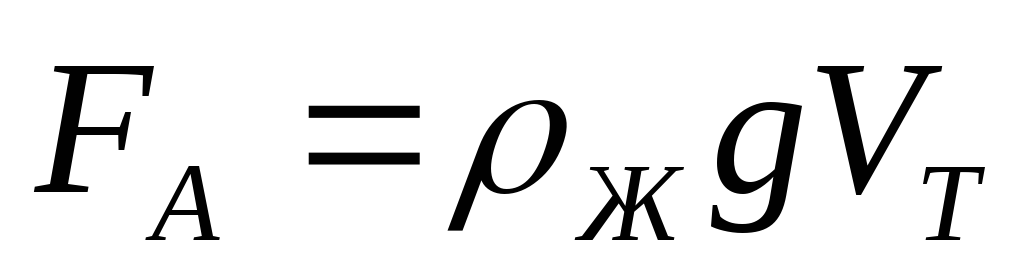 ,
равная весу жидкости в объеме
,
равная весу жидкости в объеме (
(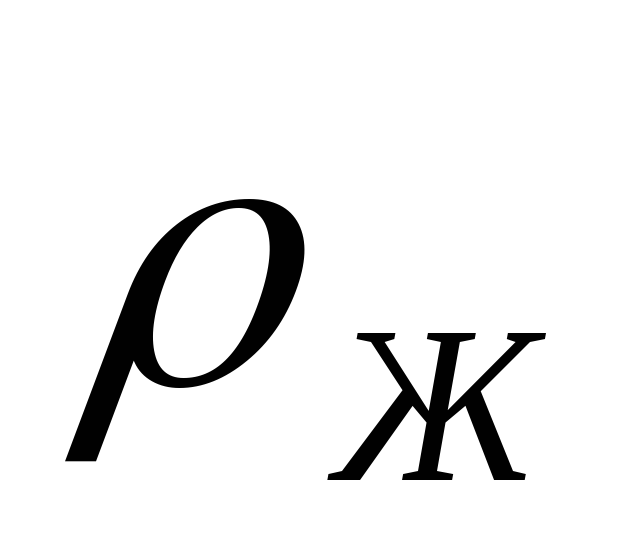 ‑плотность
жидкости);
‑плотность
жидкости);сила сопротивления со стороны жидкости (сила Стокса)
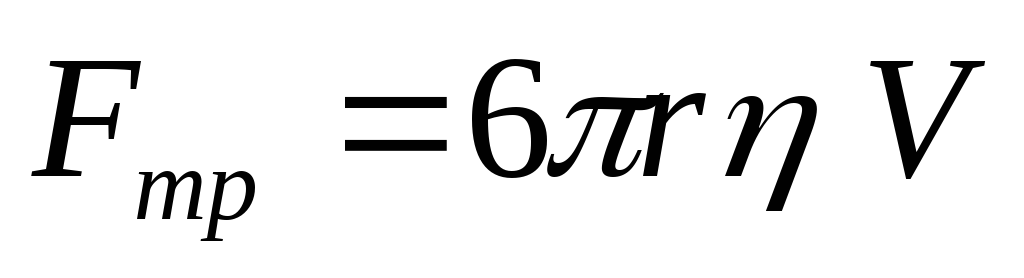 .
.
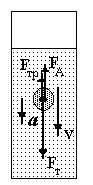
Рис. 2.
Движение шарика в вязкой жидкости
Равнодействующая этих сил обеспечивает шарику, согласно второму закону Ньютона, ускорение:
|
|
(3) |
Таким
образом, скорость шарика υ
с течением времени растет, а следовательно,
растет и сила сопротивления
![]() со стороны жидкости, пропорциональная
модулю скорости. Когда
со стороны жидкости, пропорциональная
модулю скорости. Когда![]() возрастет настолько, что сумма сил
возрастет настолько, что сумма сил![]() и
и![]() уравновесит силу тяжести
уравновесит силу тяжести![]() ,
движение шарика станет равномерным (a
= 0), т.е. с постоянной скоростью
,
движение шарика станет равномерным (a
= 0), т.е. с постоянной скоростью
![]() = const.
= const.
Измеряя
на опыте установившуюся скорость падения
шарика
![]() и радиус шарика
и радиус шарика![]() ,
зная значения плотностей материала
шарика
,
зная значения плотностей материала
шарика![]() и жидкости
и жидкости![]() ,
в которой он движется, можно определить
коэффициент внутреннего трения
(коэффициент вязкости) жидкости по
формуле:
,
в которой он движется, можно определить
коэффициент внутреннего трения
(коэффициент вязкости) жидкости по
формуле:
|
|
(4) |
