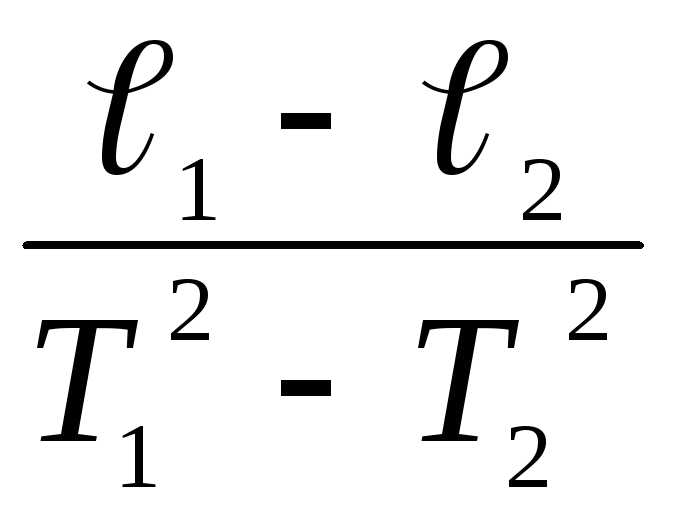Контрольные вопросы:

1. Чем обусловлены случайные и систематические ошибки.

2. Как производится вычисление погрешностей при прямых и косвенных измерениях.

3. Что называется плотностью вещества.

4. В каких приборах используется линейный нониус.

5. Как производятся измерения штангенциркулем, микрометром и на технических весах.

Лабораторная работа № 1-1 Определение ускорения свободного падения

Цель работы: исследование колебательного движения математического маятника, расчет ускорения свободного падения.

Оборудование:

1. Математический маятник переменной длины;

2. Секундомер;

3. Линейка (или мерная лента).

Краткая теория

Математическим маятником называется система, состоящая из невесомой нерастяжимой нити длиной l, на которой подвешена материальная точка массы .

Если маятник отклонить от положения равновесия на некоторый угол (см. рис. 1) и предоставить ему свободно двигаться, то под действием двух сил (силы тяжестии силы натяжения нити) маятник будет колебаться около положения равновесия (силой сопротивления со стороны воздуха будем пренебрегать).

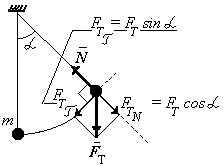
Рис. 1.

Математический маятник

Разложим силу тяжести на две составляющие по двум взаимно перпендикулярным направлениям:

вдоль нити:

(1)

перпендикулярно к ней (по касательной к траектории, т.е. к окружности):

(2)

Тангенциальная составляющая силы тяжести определяет тангенциальную составляющую ускорения :

(3)

(4)

Знак "–" свидетельствует о том, что направления тангенциальной составляющей ускорения противоположно по знаку угловому смещению маятника из положения равновесия.

Смещение маятника из положения равновесия можно характеризовать как величиной угла отклонения от положения равновесия , так и длиной дугиS (траектория движения материальной точки является дугой окружности радиуса ). Если угол выражен в радианах, то

S =

(5)

и, следовательно

(6)

для малых углов, выраженных в радианах

(7)

и из (6) – (7) следует:

(8)

Ускорение является второй производной от смещения, т.е. , поэтому:

(9)

Введем обозначение:

= 2

(10)

Подставляя (10) в (9) , получим уравнение движения математического маятника, являющееся однородным дифференциальным уравнением второго порядка:

(11)

Решение этого уравнения может быть представлено в виде:

(12)

или

(13)

(в этом можно убедиться, непосредственно подставляя (12) в (11)).

Таким образом, колебание маятника является гармоническим (т.е. смещение маятника от положения равновесия меняется с течением времени по закону синуса или косинуса). В формулах (12), (13):

А – амплитуда колебания (модуль наибольшего отклонения колеблющейся величины от равновесного значения S =0);

T – период колебания (время, за которое совершается одно полное колебание);

 = 1/ T – частота колебаний (число колебаний в единицу времени);

 = 2  Т – циклическая (угловая, круговая) частота (число колебаний за 2 секунд) ;

 = t + ₀ – фаза колебания (выражение, стоящее под знаком синуса или косинуса). Фаза однозначно определяет при заданной амплитуде в любой момент времени значение колеблющейся величины.

₀ – начальная фаза колебания (при t = 0). Слово "фаза" – греческого происхождения, означает ступень, стадию развития какого–либо явления: по значению фазы можно определить, какая часть периода прошла от момента начала колебания:  = 2t / T (при ₀ = 0). Откуда t = T/(2) .

Таким образом, период колебаний маятника T = ; где, согласно (10),. Или

T = 2

(14)

где l – длина математического маятника, g – ускорение свободного падения.

Таким образом, при малых начальных отклонениях от положения равновесия период колебаний математического маятника определяется только его длиной и ускорением свободного падения и не зависит от его массы, а также от начального отклонения от положения равновесия.

С другой стороны , T = , где t – время N полных колебаний. Эти соотношения могут быть использованы для расчета ускорения свободного падения:

(15)

Если измерение длины маятника затруднено, это осложнение легко обойти, измерив периоды колебаний Т₁ и Т₂ и разность длин маятников (– ) в этих экспериментах:

T1 = 2 и T2 = 2.

(16)

Отсюда

g = 4 2

(17)