Геометричний зміст модуля і аргументи похідної комплексної функції

Нехай диференційована в точці, тоді, де,– відстані між,на площиніі їх образами, на площині. Тоді– коефіцієнт розтягу векторапри відображенніплощинина площину.

Геометричний зміст модуля похідної: – коефіцієнт розтягу в точціпри відображенніплощинина площину.

Нехай відображає площинуна площинуі диференційована в точці.

Розглянемо криву і образпри відображенніпозначимо.

Якщо , то,– січна,– січна,– кут нахилу січноїдо,– кут нахилу січноїдо.

При січні,прямують до дотичних в точках,до кривихівідповідно, а,до кутівіміж відповідними дотичними і осями,відповідно. Тоді, тобто. Звідси – кут повороту дотичної до кривої в точціплощинипри переході до її образуі к точці.

Приклад

–відображає площину на площину. При цьому, тобтоі, тобто при відображенні площинарозтягується враз і повертається на кут –.

Вправи

Знайти коефіцієнт розтягнення і кут повороту при заданих відображеннях в заданих точках

1. ;

2. ;

3. .Знайти , в яких коефіцієнт розтягнення дорівнює 1.

Яка частина комплексної площини розтягується, а яка стискається (вправи 4, 5, 6).

4. ;

5. ;

6. ;

7. . Знайти, в яких кут повороту дорівнює нулю.

Означення аналітичної функції. Поняття Конформного відображення

Означення: Функція диференційована в кожній точці областіназиваєтьсяаналітичною в області .

Означення: Функція називається аналітичною в точці, якщо вона аналітична в деякому околі точки.

З властивостей похідної слідує, що справедливі твердження:

1) якщо ,аналітичні в, то– аналітична всюди, де;

2) якщо ваналітична, ааналітична в області, що є образомпри відображенні, то функціяаналітична в:

3) якщо аналітична ві, , то в областізначень функціївизначена обернена функція– аналітична в, причому.

Приклад 1

–аналітична () у всій площині окрім точки.

Приклад 2

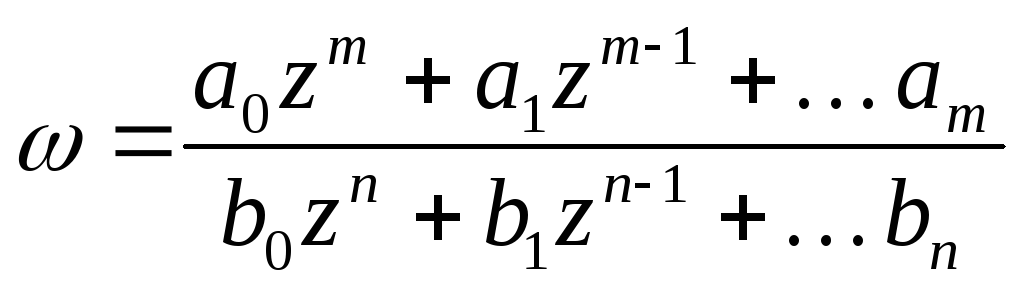–аналітична функція окрім точок , в яких знаменник перетворюється в нуль.

Нехай відображає площинуz у площину . Розглянемо на площиніz дві довільні гладкі криві , які перетинаються у точці.

Якщо при відображенні кривіпереходять у кривівідповідно (перетинаються у точці), кути між кривимиу точціта кривимиурівні, то кажуть, що відображенняу точцімає властивість збереження кутів.

Нехай відображення площиниz у площину . Розглянемо у площиніz трикутник з вершиною в точці та довільними нескінченно малими лінійними елементами,, які виходять з. Якщо при відображеннівін переходе у трикутник з вершиною в точці, який подібний вихідному, з точністю до нескінченно малої більш високого порядку, ніж сторони вихідного трикутника, то кажуть, що відображенняв точцімає властивість постійності розтягування.

Означення: Взаємо-однозначне відображення області комплексної площиниz на область D комплексної площини називаєтьсяконформним, якщо це відображення у всіх точках zмає властивість збереження кутів і постійності розтягування.

Якщо кути при відображені не змінюють направлень, то кажуть про конформне відображення І-го роду. Якщо кути змінюють направлення на протилежні, то кажуть про конформне відображення ІІ-го роду.

Крім того, кажуть, що відображення конформне унескінченно віддаленій точці, якщо відображає початокz=0 конформно у площину .

Теорема: Для того, щоб функція реалізувала конформне відображення І-го роду області, необхідно і достатньо, щоб в цій області функціябула:

1. однолистою;

2. аналітичною;

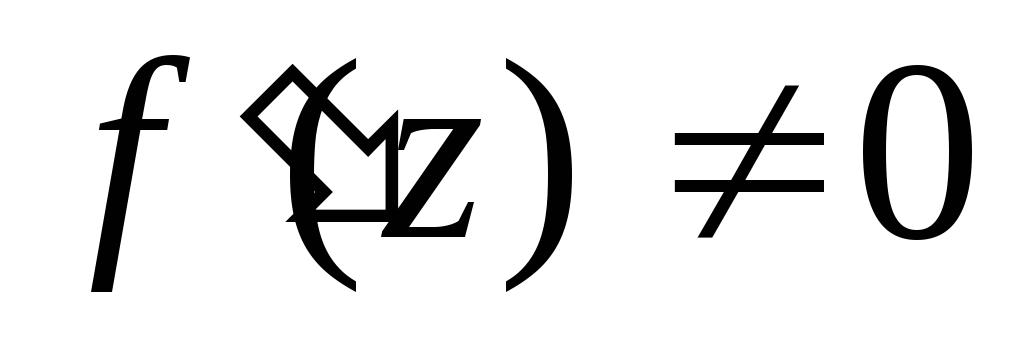3. для будь-якого z;

Доведення: див. [2, с. 107], [1, 146].

Приклад 1: відображає площинуz на конформно, бо.

Приклад 2: дзеркальне відображення відносно осіOx, змінює напрям кутів на протилежний. Таким чином – конформне відображення ІІ-го роду (хоча функція не аналітична!)

Вправи

Знайти точки, в яких відображення конформне (І-го роду).

1) ;

2);

3);

4).

Чи конформні відображення у нескінченно віддаленій точці

5);

6) ;

7) ;

8).

Покажіть, що відображення здійснюють конформне відображення ІІ-го роду

9);

10) , задовольняє теоремі.