Лекція №17. Рівняння еліптичного типу

1. Постановка крайових задач.

Розглянемо стаціонарне теплове поле. Розподіл температури буде задовольняти рівнянню (враховуючи, що )або(рівняння Лапласа)

Задача про стаціонарний розподіл тепла всередині тіла Т формулюється наступним чином:

Знайти функцію що задовольняє всередині Т рівнянняі граничній умові, одного з наступних видів:

1. на поверхні(перша крайова задача),

2. на- похідна у напрямку нормаліп до поверхні (друга крайова задача),

3. на(третя крайова задача).

Першу крайову задачу називають задачею Дирихлє, а другу – задачею Неймана.

Крім того, якщо розв’язок шукається в внутрішній (в зовнішній) по відношенню до частини, то відповідно задачу називають внутрішньою (зовнішньою) крайовою задачею.

Розглянемо задачу на площині, тобто для двох змінних. Відмітимо, що функції і(двох змінних), для яких виконується умова Коші-Рімана(що називаються гармонійними) будуть задовольняти однорідному рівнянню.

Гармонійна функція, задовольняє принципу міні-максимуму (див. теорію аналітичних функцій), таким чином для першої крайової задачі буде виконуватись теорема єдиності, як це ми доводили раніше.

2. Перша крайова задача для круга. Інтеграл Пуассона.

Розглянемо задачу.

Знайти функцію , що задовольняє рівняннювсередині (або за межами) круга і граничній умовіна границі круга радіусаa.

Переходячи до полярної систему координат з початком у центрі кола отримаємо рівняння, в полярних координатах у вигляді

.

Розв’язок шукається методом розділенням змінних .

Підставляючи до рівняння отримаємо або

.

Звідси . Враховуючи періодичність і,- періодична, а це можливо тільки якщо, тобто.

Функцію розшукують у вигляді. Підставляючи в рівняння і скорочуючи на, знайдемоабо. Отже

Розв’язок: для (внутрішня задача) мають вигляд

(, так як прифункціянеобмежена і не буде гармонійною), ідля(зовнішня задача) (, так як прифункціянеобмежена).

Звідси (внутрішня задача)

( зовнішня задача).

Для визначення ікористуються граничними умовами.

Остаточно будемо мати (внутрішня задача)

Для зовнішньої задачі .

Отримані формули можна спростити. Для внутрішньої задачі розглянемо більш детально ситуацію.

. Для зовнішньої задачі отримаємо .

Отримані інтеграли називаються інтегралами Пуассона.

Відзначимо, що інтеграл Пуассона дає розв’язок крайової задачі для кусочно неперервної функції (дивіться [5]).

3. Частинний розв’язок рівняння Лапласа.

Цікавість представляє розв’язок рівняння Лапласа, що володіє циліндричною симетрією (тобто, залежать виключно від , наприклад при граничних даних, що не залежать від).

Рівняння прийме вигляд отже.

Приклад. Знайти розподіл тепла на кільці , якщо.

Розв’язок. Оскільки граничні умови не залежать від тотоді виконуються рівності,. Отжеі маємо.

Практичне заняття №11. Параболічні та еліптичні рівняння

Необхідні відомості: 1. Розв’язання першої крайової задачі для параболічного рівняння.

2. Розв’язання параболічного рівняння на осі та напівосі. Інтеграл Пуассона.

3. Розв’язок рівняння Лапласа. Інтеграл Пуассона.

Задачі.

1.1 Розв’язати рівняння , якщо

.

1.2 Розв’язати ,, якщо

1.3 Розв’язати ,, якщо

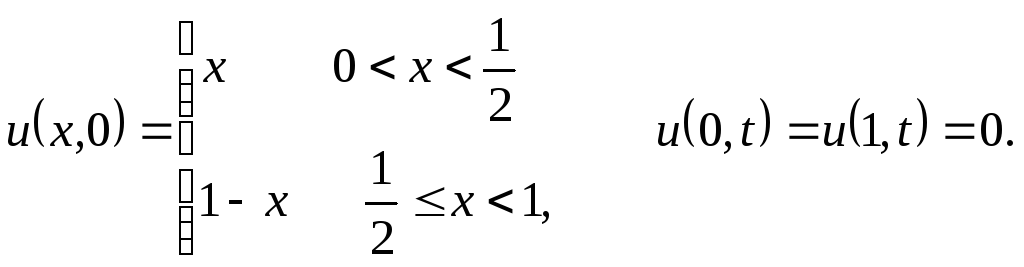
2.1 Знайти стаціонарний розподіл тепла на пластині у формі круга радіуса 1, якщо верхня половина має температуру , а нижня.

2.2 Знайти розподіл тепла на кільці , якщо

.

Задачі для самостійної роботи.

1. Розв’язати ,,, якщо

2. Розв’язати рівняння , якщо

.

3. Знайти розподіл тепла для напівскінченного стержня, якщо лівий край х=0 теплоізольовано, а початкова умова: ,

(дивіться задачу 2).

4. Розв’язати ,, якщо

5. Розв’язати ,, якщо

6. Розв’язати ,, якщо.

7. Знайти розподіл тепла на кругу радіуса , якщо на граничному колі підтримується температура

8. Знайти розподіл тепла на кільці , якщо.

9. Знайти стаціонарний розподіл тепла у тонкому стержні з темплоізольованою боковою поверхнею, якщо на кінцях ,.

10. Знайти розв’язок рівняння Лапласа, для внутрішньої частини кільця , що задовольняє крайовим умовам

(перейти до полярних координат, та з’ясувати у якому вигляді треба шукати розв’язок).

11. Знайти розв’язок рівняння Лапласа для внутрішньої частини кільця , що задовольняє крайовим умовам

, .

12. Розв’язати задачу 11 для крайових умов

, .