86

Зміст

Лекція №1.Означення диференціального рівняння і розв’язку. Задача Коші. Теорема існування та єдиності розв’язку задачі Коші 2

Лекція №2. Рівняння з розділеними змінними. Однорідні рівняння 4

Практичне заняття №1. Рівняння з розділеними змінними 6

Практичне заняття №2. Однорідні рівняння 8

Лекція №3. Лінійні рівняння першого порядку. Рівняння Бернуллі та Рікатті-Буля 10

Практичне заняття №3.Лінійні рівняння першого порядку. Рівняння Бернуллі 12

Лекція №4.Особливі точки. Особливі рішення. Рівняння Клеро 14

Практичне заняття №4. Рівняння Клеро 17

Лекція №5. Системи диференціальних рівнянь першого порядку. Теорема існування та єдиності розв’язку задачі Коші. Рівняння п-го порядку 18

Практичне заняття №5. Рівняння п-го порядка. Способи зниження порядка 20

Лекція №6. Лінійні рівняння n-го порядку. Системи лінійно незалежних функцій 21

Лекція №7. Формула Остроградського – Ліувілля. Лінійні однорідні рівняння з постійними коефіцієнтами 24

Практичне заняття №6. Лінійне однорідне рівняння. Формула Остроградського – Ліувілля. Лінійні однорідні рівняння з постійними коефіцієнтами 27

Лекція №8. Лінійні неоднорідні рівняння n - го порядку. Застосування рівнянь у теорії коливань. Резонанс 28

Практичне заняття №7. Неоднорідні лінійні рівняння 32

Лекція №9. Системи п звичайних диференційних рівнянь. Лінійні рівняння з частинними похідними першого порядку 33

Практичне заняття №8. Система диференційних рівнянь. Диференційні рівняння у частинних похідних першого порядку 38

Лекція №10. Класифікація рівнянь у частинних похідних другого порядку. Диференційні рівняння з двома змінними 41

Лекція №11. Рівняння гіперболічного типу. Постановка крайової задачі. Теорема єдиності розв’язку 47

Лекція №12. Редукція, загальної задачі. Задачі на прямій і напівпрямій. Формула Даламбера, метод продовження 52

Практичне заняття №9. Типи рівнянь другого порядку у частинних похідних. Рівняння коливання струни. Формула Даламбера 57

Лекція №13. Неоднорідні гіперболічні, рівняння на прямій і піввісі. Метод Фур’є розділення змінних 60

Лекція №14. Перша крайова задача для гіперболічного рівняння 65

Практичне заняття №10. Метод Фур’є. Гіперболічні рівняння 68

Лекція №15. Рівняння параболічного типу 71

Лекція №16. Перша крайова задача для рівняння параболічного виду 74

Лекція №17. Рівняння еліптичного типу 78

Практичне заняття №11. Параболічні та еліптичні рівняння 81

Література: 84

Лекція №1.Означення диференціального рівняння і розв’язку. Задача Коші. Теорема існування та єдиності розв’язку задачі Коші

1.Означення диференціального рівняння і розв’язку.

Означення. Вираз виду F(,)=0 де– незалежна змінна, а– незалежна функція від цієї змінної,- похідні цієї функції, називається диференціальним рівнянням у звичайних похідних.

По порядку найвищої похідної визначається порядок рівняння.

Означення. Функція визначена на довільній множині, називається рішенням рівняння на даній множині, якщо при підстановці функції в рівняння воно звертається у вірну тотожність.

Приклад. y′=y=kx, k=const

2.Геометрична інтерпретація, диференціального рівняння першого порядку.

Нехай y′=f(x,у) - рівняння першого порядку, що розв’язано відносно похідної. В кожній точці (x,у) декартової площини побудуємо вектор з кутом нахилу ,до додатної частини осі ОХ, для якого виконується рівність .

Сукупність всіх векторів називають полем напрямків, що задається рівнянням y′=f(x,у).

Поле напрямків є геометричною інтерпретацією диференціального рівняння першого порядку.

Якщо розв’язок рівняння y′=f(x,у), то у точці відповідний напрямок з кутом , для якого , буде співпадати з дотичною до графіка кривоїз точкою дотику.

Отже, якщо є рішенням рівняння, то напрямок, проведений до кожної точки кривої, збігається з дотичної, проведеної в цій точці до кривої.

Iнтегральною кривою будем називати криву у якої дотична до будь-якої точки співпадає з напрямком проведеним до цієї точки.

Геометрична інтерпретація рішення - це той факт, що рішення є інтегральною кривою.

3. Загальні рішення диференціального рівняння. Задача Коші.

Означення. Функція y=φ() називається загальним рішенням диференціального рівняння n-го порядку, де – довільні константи, якщо воно є рішенням даного рівняння й будь-яке інше рішення можна одержати з даної функції шляхом відповідного вибору констант.

Припустимо, що треба знайти розв’язок рівняння який задовольняє умовам:

Такі умови називають початковими умовами, а задачу – задачею Коші. Для розв’язку задачі Коші треба знайти загальний розв’язок, а потім використовуючи початкові умови, знайти ті значення констант при яких розв’язок буде задовольняти початковим умовам.

Приклад. Точка рухається уздовж осі зі швидкістю υ(t). При t=0, точка перебуває в. Знайти положення точки в довільний момент часу.

Нехай - координата точки у довільний момент часу, тоді маємо

.

Отже . Використовуючи початкову умовуотримаємо.

4. Теорема існування та єдиності розв’язку задачі Коші.

Розглянемо - задачу Коші для рівняння першого порядку.

Теорема. Нехай функція f(x,у) визначена й неперервна в області і за зміноюу задовольняє умову Ліпшица: для будь-якого х і будь-яких виконується нерівність,М – константа. Тоді існує таке, що длязадача Коші має єдине рішення, графік якого знаходиться в областіD, причому,,), де.

Доведення. Нехай у=у(х) розв’язок задачі Коші, тоді і інтегріруя отримаємо рівність, отжеу=у(х) є рішенням інтегрального рівняння .

_{Навпаки, якщо у=у(х) розвязок інтегрального рівняння, то диференціруя його отримаємо, що} у=у(х) – розв’язок задач Коші.

Таким чином, диференціальне рівняння й інтегральне рівняння - еквівалентні. Доведення теореми еквівалентно доведенню того, що інтегральне рівняння має рішення й воно єдине.

Розглянемо простір неперервних функцій , графіки яких з областіD на цьому відрізку не виходять, на якому визначена метрика . Покажемо, що- повний простір. Нехайпослідовність Коші в. З курсу аналза відомо, щозбігаються до неперервно функції,. Доведемо включення, для цього треба показати, що графікне виходить з областіD. Оскільки (графік в областіD), то переходячи до границі при п→∞ отримаємо ,, тобто.У цьому просторі розглянемо відображення: яке неперервну функцію у(х), в силу властивостей інтеграла, відображає у неперервну. З рівності || ≤≤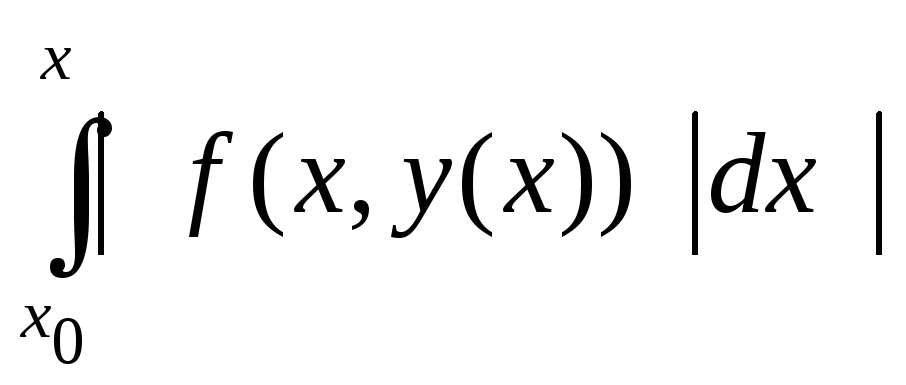N|| =. Маємо, що графік функціїAy не виходить за область D. Отже А:.

Доведемо, що А стискаюче відображення. Візьмемо і розглянемоρ(Ay,Аz)=|-|≤||≤|| ≤M∙ ρ(y, z) || ≤, деα=М∙ h<1.

Отже відображення А є стискаючим відображенням і на підставі принципу стискаючих відображень воно має єдину нерухливу точку. Тобто, існує y(x), що є неперервною на відрізку функцією графік якої не виходить з областіD, яка задовольняє рівності:

, тобто .

Значить задача Коші має єдине рішення. Теорема доведена.

Зауваження до теореми. Якщо частинна похідна обмежена на області D, то умова Ліпшица виконується.