ZADANIYa-zaochn-FVMiZ-2015-2016-uch-god / НАПРАВЛЕНИЕ ПОДГОТОВКИ / ЗООТЕХ- бак / 1 зоо / математика Зоотехния

параметрами определяется нормальное распределение? Каков их вероятностный смысл?

2.Начертите нормальную кривую. Каков геометрический смысл параметров нормального распределения? Как влияет изменение математического ожидания и среднего квадратического отклонения на форму нормальной кривой?

3.Как вычислить вероятность попадания в заданный интервал значений нормально распределенной случайной величины?

4.В чем заключается правило «трех сигм»? Как найти диапазон изменения значений нормально распределенной случайной величины?

Решение типовой задачи Задача. Для коров холмогорской породы удой за лактацию – случайная ве-

личина, распределенная по нормальному закону с математическим ожиданием а = 3200 кг и средним квадратическим отклонением =300 кг. Каков процент животных, удои которых за лактацию заключены в пределах от 3000 кг до 3500 кг? В каком диапазоне на-

блюдаются удои?

Решение.

Найдем вероятность, с которой случайная величина (удой за лактацию) принимает значение в интервале (3000; 3500). Для этого воспользуемся формулой, позволяющей вычислить вероятность попадания нормально распреде-

0,3413 0,2454 0,5867 0,59 ,

т. е. 59% коров будут иметь удои в пределах от 3000 кг до 3500 кг.

Правило «трех сигм» позволяет утверждать следующее: практически достоверно, что значения любой нормально распределенной случайной величины X расположены в интервале (а – З , а + З ). В нашей задаче a – 3= 3200 – 900= 2300; а + З= 3200 + 900=4100.

Таким образом, для коров данной породы удои за лактацию будут колебаться от 2300 кг до 4100 кг.

21

Тема VI. Простейшие приемы обработки выборочных данных и оценка параметров распределения

Литература: [4], гл. XV, § 1 – 6, 8, задачи 2, 3; гл. XVI, § 1 – 10, 13 – 16, зада-

чи 1 – 4.

Первичная статистическая информация представляет собой ряд значений, записанных в той последовательности, в которой они были получены.

Чтобы придать этой информации обозримую и удобную для изучения форму, используют ряды распределения и их графическое изображение – полигон и гистограмму. Важнейшей числовой характеристикой распределения является среднее значение.

Свойство животных или растений отличаться друг от друга даже в однородной совокупности (на одной ферме или на одном поле) принято называть изменчивостью (варьированием). Изменчивость признака характеризуют дисперсия и среднее квадратическое отклонение.

Коэффициент вариации позволяет сравнивать изменчивость признаков, выражаемых в разных единицах измерения (например, высоты и массы). Обычно его выражают в процентах. Изменчивость считается значительной, если коэффициент вариации больше 20%, средней, если коэффициент вариации больше 10%, но меньше 20%, и незначительной, если коэффициент вариации меньше 10%. Выборочные характеристики позволяют делать оценки генеральных параметров по данным обследования выборки.

В этой теме необходимо усвоить:

1)методику группировки выборочных данных и представления их в виде ряда распределения;

2)графическое представление ряда распределения;

3)методику вычисления основных выборочных характеристик;

4)методику оценивания генеральной средней с помощью доверительного интервала.

Вопросы для самопроверки

1.Поясните на примерах понятия генеральной совокупности и выборки.

2.Приведите примеры варьирующих признаков (случайных величин) и вариант выборки.

3.Что такое вариационный ряд распределения? Как определяется относительная частота варианты?

4.Как строится гистограмма относительных частот распределения? Чему равна ее площадь?

5.Перечислите основные выборочные характеристики. Как они вычисляются?

6.Что характеризуют дисперсия и среднее квадратическое отклонение?

7.Для каких целей используется коэффициент вариации?

8.Что характеризует ошибка средней S x ?

9.Что понимают под доверительным интервалом для оценки генеральной

22

средней x Г ? Как найти доверительный интервал при заданной надежности (доверительной вероятности) ?

10.Как изменится величина доверительного интервала, если увеличить надежность ?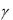

11.Что понимают под представительностью (репрезентативностью) выборки? Как достигается представительность выборки при отборе?

12.Как вычислить выборочную среднюю и дисперсию в случае сгруппированных данных?

13.Были установлены следующие показатели высоты в холке (см): для те-

_

лят x =60, = 3; для молодых коров х = 100, = 5. Отличаются ли они по степени изменчивости?

14. Промеры глубины груди симментальского скота (n=168) дали сле-

Решение типовой задачи Задача. Из крупного стада коров произведена случайная выборка, получено

20 вариант удоя коров за 300 дней лактации (в ц): 35,9; 35,3; 42,7; 45,2; 25,9; 35,3; 33,4; 27,0; 35,9; 38,8; 33,7; 38,6; 40,9; 35,5; 44,1; 37,4; 34,2; 30,8; 38,4; 31,3.

Требуется:

1.получить вариационный ряд и построить гистограмму относительных частот;

_

2. найти основные выборочные характеристики: x , s2 , s, V, s_ ;

x

3. с надежностью 95% указать доверительный интервал для оценки

_

генеральной средней x Г .

Решение.

1.Запишем исходные данные в виде ранжированного ряда, т. е. располагая их в порядке возрастания:

25,9; 27,0; 30,8; 31,3; 33,4; 33,7; 34,2; 35,3; 35,3; 35,5; 35,9; 35,9;

37,4; 38,4; 38,6; 38,8; 40,9; 42,7; 44,1; 46,2.

Максимальное значение признака составляет 46,2 ц, а минимальное – 25,9 ц. Разница между ними составляет 20,3 ц. Этот интервал надо разбить на определенное количество классов. При малом объеме выборки (20 – 40 вариант) намечают 5 – 6 классов. Возьмем длину классового интервала xi 5 .

Получаем пять интервалов: первый 25 – 30, второй 30 – 35, третий 35 – 40, четвертый 40 – 45, пятый 45 – 50 (начало первого класса не обязательно должно совпадать со значением минимальной варианты).

С помощью ранжированного ряда определим частоту попадания вариант выборки в каждый интервал. В первый интервал попадет два значения

23

(25,9 и 27,0), поэтому m1 = 2. Во второй интервал попадают пять значений, поэтому m2 = 5. Аналогично m3 =9, m4 =3, m5 =1.

Теперь найдем относительные частоты попадания вариант выборки в каждый интервал:

Для проверки вычисляем сумму относительных частот:

Тот факт, что в сумме получили единицу, подтверждает правильность вычислений. По формуле:

P1/ xi1

вычислим плотности P1/ относительных частот вариант. Получаем:

24

Строим гистограмму относительных частот – ступенчатую фигуру, состоящую из прямоугольников, основаниями которых являются классовые интервалы, а высотами – соответствующие значения плотностей относительных частот P1/ , Классовые интервалы изображают на оси абсцисс, а значения P1/ откладывают на оси ординат.

Для нашего примера гистограмма относительных частот изображена на рисунке 4.

2) Основные выборочные характеристики вычисляются по формулам:

таблицы под соответствующим столбцом. Разделив эту сумму на 20, получим

_

x 36,015 36,0.

Теперь заполняем следующий столбец таблицы, в который записываем

Если разности вычислены правильно, то их сумма равна нулю.

Затем возводим эти разности в квадрат и заполняем последний столбец

Извлекая с помощью таблиц или микрокалькулятора квадратный корень из величины s2 , находим:

Вычисляем коэффициент вариации

V5,08 100% 14%.

36

Поскольку 10% < V < 20%, то изменчивость удоев за 300 дней следует считать средней.

3) Доверительный интервал для оценки генеральной средней определяется как

x tSx xГ x tSx ,

26

где величина t при заданной надежности определяется с помощью таб-

лиц приложения 2.

В нашем примере: t t( ; n) t(0,95;20) 2,10.

Вычисляем теперь радиус доверительного интервала: t sx 2,101,34 2,8.

Таким образом, с надежностью 95% можно утверждать, что во всем стаде средний удой за 300 дней (генеральная средняя) заключен в пределах

Тема VII. Корреляция и регрессия

Литература: [4], гл. XVIII, § 1 – 9, задачи 1, 2.

В некоторых исследованиях важно установить, изменяются ли два признака (случайные величины) независимо друг от друга, или же изменение одного из них каким-то образом связано с изменением другого. На сам факт такой связи (или на ее отсутствие) указывает значение коэффициента корреляции.

Уравнение регрессии позволяет предсказать, какие изменения (в среднем) будет претерпевать второй признак при изменении первого признака. Понятия коэффициента корреляции и коэффициента регрессии играют важную роль в совместном изучении двух случайных величин, поэтому необходимо усвоить методику их вычисления.

Вопросы для самопроверки

1.Что понимают под корреляционной зависимостью? Чем она отличается от функциональной зависимости?

2.Что собой представляет корреляционная таблица (корреляционная решетка)? В каких случаях целесообразно ее составление?

3.Что такое корреляционное поле?

4.Сформулируйте две основные задачи корреляционного анализа.

5.Что характеризует коэффициент корреляции? Какие значения он может принимать?

6.Что можно сказать о связи между двумя случайными величинами, если коэффициент корреляции равен нулю? равен единице?

7.Какая разница между положительной и отрицательной корреляцией?

8.Как получают эмпирическую линию регрессии?

9.Какую форму имеет линия регрессии в случае линейной корреляцион-

ной зависимости?

10.Запишите уравнение прямой регрессии. Как можно построить эту прямую?

11.Что характеризует коэффициент регрессии?

12.При изучении зависимости между живым весом коров-первотелок и их удоями за нормированную лактацию был вычислен коэффициент рег-

27

рессии by / x 6,9 . Какого увеличения удоев в среднем можно ожидать при увеличении веса коров-первотелок на 10 кг?

Решение типовой задачи Задача. Для 10 петушков леггорнов 15-дневного возраста были получены следующие данные о весе их тела X (г) и весе гребня У (мг):

Требуется:

1.найти коэффициент корреляции и сделать вывод о тесноте и направлении линейной корреляционной связи между признаками;

2.составить уравнение прямой регрессии;

3.нанести на чертеж исходные данные и построить полученную прямую регрессии.

Решение.

1) В случае малых выборок расчет коэффициента корреляции можно проводить по формуле:

Промежуточные вычисления удобно располагать в виде таблицы.

Таблица 7

28

3) Нанесем исходные данные на координатную плоскость и построим найденную прямую регрессии (рисунок 5).

Для того чтобы провести прямую в системе координат, достаточно

Отметим что полученная математическая модель (уравнение прямой регрессии) обладает прогнозирующими свойствами лишь при изменении переменной x от 69 до 95. Так, например, можно с достаточной степенью достоверности считать, что при весе 80 г все его гребня составит

y 2,3280 132,56 53мг.

30