Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Орловский филиал РАНХиГС

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

МАТЕМАТИЧЕСКИЙ ПРАКТИКУМ

.pdf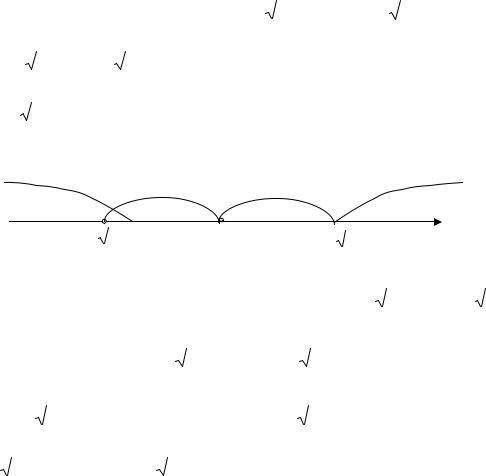

Скачиваний:

Добавлен:

04.03.2016

Размер:

3.05 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2011 12 13 14 15 16 17 18 19 20 > Следующая >>>

Имеем

lim

4x2 +

= +∞ ;

lim

4x2 +1

= −∞ .

x→3+ x − 3

x→3− x −

f (−x) =

4(−x)2

2 +1

≠ f (x);

f (−x) ≠ f (x)

функция общего

(−x) −

− x − 3

вида, непериодичная.

(4x2 +1)′(x − 3) − (4x2

y′

+1)(x − 3)′

8x(x − 3) − (4x2 +1)

4x2 − 24x −1

(x − 3)2

12 ±

y′ = 0 4x2 − 24x −1 = 0 x

144 + 4

148

1,2

12 +

6 +

148

≈ 6,035

6 −

≈ −0,035.

Исследуем знак y′

методом интервалов:

y′

6 −

6 +

6 −

6 +

Функция возрастает

на

интервалах

− ∞;

;

;+∞

6 +

6 −

убывает на интервалах

;3 ;

6 +

6 −

- точка минимума, x

- точка максимума.

6 +

6 −

≈ 48,5;

≈ −0,331.

y′′ =

(8x − 24)(x − 3)2 − 2(x − 3)(4x2 − 24x

−1)

= .

(x − 3)4

(8x − 24)(x − 3) − 2(4x2 − 24x −1)

(x − 3)3

Исследуем знак y′′ .

101

_			Функция	выпукла	на
_	+		интервале
y”:	+	х	интервале
3		х	(−∞;3) ,	вогнута	на
3			(−∞;3) ,	вогнута	на
			интервале	(3;+∞)

7.Точек перегиба нет.

8.Находим наклонную асимптоту y = kx + b :

k =

lim

f (x)

= lim

4x2 +1

lim

4x2

= 4

x→∞ x

x→∞ x(x − 3) x→∞ x

2 − 3x

lim [f (x) − kx]=

4x2

12x +1

b =

lim

− 4x

lim

= 12

x − 3

− 3

x→∞

x→∞ x

y = 4x +12наклонная асимптота.

9. Точки пересечения с осями координат:

Если x = 0 y = −

M 0;−

- точка пересечения с осью 0y .

Если y = 0 4x2 +1 = 0 точек пересечения с осью 0x нет. Строим график функции:

y	y = 4x +12

48,7

	12
	-3 0	3		х
	1	6 +
−			37
			37
	3
	3		2
			2
		x=3

Пример 3. Написать уравнение касательной и нормальной прямых к

линии y = sin 2x в точке x	= π .
0	6

Уравнение касательной прямой к графику y = f (x) в точке x = x0 имеет вид:

y − f (x0) = f ′(x0)(x − x0).

Уравнение нормальной прямой в той же точке имеет вид:

102

y − f (x ) = −

(x − x ) .

′(x0)

Для функции y = sin 2x

получаем:

′

f (x) = 2cos2x .

Отсюда f ′(x0) = 2cos2 π = 2cosπ = 1.

) = sin 2 π

= sin π =

f (x

Теперь

имеем:

y −

= 1 x −

или

y = x +

−

уравнение

касательной прямой,

y −

= −

−

или y = −x +

- уравнение нормальной прямой.

Пример 4. Используя понятие дифференциала функции вычислить

приближенно e−0,2 .

Имеем

формулу

f (x) ≈ f (x0) + f ′(x0)(x − x0) в качестве

f (x) берем

y = e

, а в качестве x0

′

= (e

′

, поэтому получаем:

f (x)

) = e

e−0,2 ≈ e0 + e0(−0,2) = 1− 0,2 = 0,8

Пример 5. Используя формулу Тейлора, найти разложение функции

y = ln(2 − x2 ) в окрестности точки x = 1, удерживая при этом три члена.

Имеем

) = ln(2 −12 )= ln1 = 0

f (x) = f (x

) +

f ′(x0)

(x − x )+

f ′′(x0)

(x − x )2

+ ... f (x

f ′(x) =

− 2x

f ′(x ) = − 2 1 = −2

2 − x2

2 −1

f ′′(x) =

− 2(2 − x2 )+ 2x(−2x)

− 4 −

2x2

f ′′(x

) =

− 4 − 2

= −6

(2 − x2 )2

(2 − x2)2

Окончательно получаем:

ln(2 − x2 )= −2(x −1) −	6	(x −1)2 + ... или ln(2 − x2)= −1+ 4x − 3x2 + ...

2

Задачи для самостоятельного решения.

1. Указать промежутки возрастания и убывания функций и найти их экстремумы:

1. y =	1	x3 + x2 − 3x	2. y = x3 − 3x	3. y = x3 + 2x2 + x

3
4. y = x2 + 6x			5. y = 2x2 + 3x +1	6. y = 5x2 − 4x + 2

103

7. y =

− x2

8. y = 4x4 + 2x3 − 5x2

9. y =

x2 +1

x + 2

10.

y =

2x2 −1

11.

y =

x2 + x − 6

12.

y = x + ln(1− 2x)

(x − 5)2

x −1

13.

y = xe− x

14.

y = x2e− x

15.

y = e− x − e−2x

16.

y = ln(1+ 2x2 )

17.

y = x3ex

2. Найти наименьшее и наибольшее значение функций в заданных промежутках:

1. y = x2 − x + 4; [−1;2]						2.	y = −3x2 + 6x −1; [− 2;2]
3. y = x3 − 3x2 + 3x + 2; [− 2;3]						4.	y = 3x4			+ 4x3 +1; [− 2;1]
5.	y = x5 − x3 + x + 2; [−1;1]					6.	y =	x	+	4	; [− 5;−1]

							4			x
7.	y =	x	+	2	; [1;6]	8.	y = x3 − 3x + 2; [− 3;1,5]

9. y = x4 −8x2 + 3; [− 2;2]

10.

y =

x −1

; [0;4]

x +1

; [− 2;2]

y = 3

; [1;3]

11.

y =

4 − x2

12.

(x2 − 2x)2

13.

y = x2 ln x; [1;e]

14.

y =

;

[− 3;3]

x2 +16

15.

y = −2x2 − ln x; [1;e]

16.

y = x +

; [1;3]

; [−8;−1]

17.

y = (5− x)2−x ; [−1;0]

18.

y = 23 x2

19.

y = 2sin x + sin 2x;

3π

20.

y = cos

x + sin x;

21.

y =

cos2x + sin x;

22.

y = x + cos

23.

y = sin

x + cos

104

3. Решить задачи, используя элементы дифференциального

исчисления.

1.Число 20 разбить на такие 2 слагаемых, чтобы сумма их квадратов была наименьшей.

2.Число 180 разбить на 3 положительных слагаемых так, чтобы 2 из них относились как 1:2, а произведение 3 слагаемых было наибольшим.

3.Найти число, которое превышало бы свой квадрат на максимальное значение.

4.Требуется оградить забором прямоугольный участок земли площадью 294 м2 и затем разделить этот участок забором на 2 равные части. При каких линейных размерах участка длина всего забора будет наименьшей.

5.Определить размеры открытого бассейна с квадратным дном объемом 32 м3 так, что на облицовку его стен и дна пошло наименьшее количество материала.

6.Консервная банка данного объема имеет форму цилиндра. Каково должно быть соотношение ее размеров (высоты и диаметра), чтобы на изготовление пошло минимальное количество жести.

7.Каково должно быть отношение высоты к радиусу основания конического шатра данной вместимости, чтобы на его изготовление пошло наименьшее количество материи.

8.Найти длины сторон прямоугольника наибольшей площади, вписанный в прямоугольный треугольник со сторонами 18, 24, 30 см и имеющего с ним общий прямой угол.

4. Указать участки выпуклости и вогнутости функций и найти точки

перегиба:

1. y = x3 + 3x2 + x +1	2. y = 4x3 − 6x2 + x + 5
3. y = 2x3 + 3x2 + 7	4. y = 3x3 − 2x2 + x

105

5. y = x4 − x3 − 3x2

6. y =

− x2

7. y = 2x4 − 5x3 + 3x2

8. y = xex

9. y = xe−2x

10.

y = x2e−2x

11.

y = xe− x2

12.

y = ln(1+ x2 )

13.

y = ln(4 + 2x2 )

14.

y = ln(7 + 4x2 )

15.

y =

16.

y =

+ 4

x2 +1

5. Для нижеприведенных функций: а) найти область определения, интервалы непрерывности, точки разрыва; б) определить четность (нечетность), периодичность функций; в) найти асимптоты (вертикальные, наклонные, горизонтальные) графика; г) найти интервалы монотонности и точки экстремума; д) найти интервалы выпуклости и вогнутости графика; е) найти точки пересечения графика с осями координат; ж) построить графики:

1.	y = x3 − 4,5x2 + 6x
4.	y =	4
		+ x2
	1
7.	y = 0,5x2 (x2 − 4)

10.y = x2 − 4 x2 +1

	x	+ 2	2
13.	y =
		− 2
	x
16.	y = e− x	2
19.	y = ln(1+ x2 )

22.y = ex x +1

2. y =

(x + 2)(x − 4)2

3. y = 3x5 − 5x3

5. y = 0,25x3 − x2 − 4x +16

6. y = x3 +

8. y =

9. y =

x2 + x +1

x2 + 4

11.

y =

3x + 5

+ 2

12.

y = x2 − 4

14.

y =

15.

y =

x2 − 3x + 2

x2 − 4x + 3

17.

y = (x + 2)e−2x

18.

y = (4 − x)e

20.

y = xe− x2

21.

y = xln x

23.

y = 2x

+ 2− x

24.

y =

x2 − x − 6

x − 2

106

25.

y = 5−

− x2

26.

y =

−

−1

27.

y =

(x +1)3

x + 2 x − 2

30.

y = (x −1)2 (x − 3)3

28.

y = 3 x3 − 3x

29.

y = 2x − 3

6. Составить уравнение касательной и нормальной прямых к кривой y = f (x) в точке x= хо

1. y = 5x3 + 2x2 − x + 3; xo = 2

2. y =

; xo = 0

x +

y =

x2 +1

; x

y = ln(1+ 3x);

xo = 0

x2 + x + 3

y = sin 2x;

= π

y = (1+ x)e−2x ; xo = 0

y = ln(2ex

−1); xo

= 0

y = cos2 x; xo

= π

y = esin x ;

xo = π

10. y = x2 −

;

xo =1

11.

На параболе

y = x2 взяты две

точки

с абсциссами x

= 1; x

= 3..

Через эти точки проведена секущая. Написать уравнение касательной к данной кривой, которая параллельна проведенной секущей.

12.Касательная к кривой y = 3x − x2 перпендикулярно прямой,

проходящей через точки (2;0) и (0;1). Составить уравнение этой касательной.

13.	Составить уравнение касательных к кривой				y = x3 +1,
параллельных прямой y − 3x +1 = 0 .
14.	Составить	уравнение	касательной	к	кривой

y = ln(x −1) перпендикулярно прямой, образующей с осью ОХ угол в 135о.

15. Составить уравнение	касательной	к кривой	y =	2x − 7	,

				x − 3
проходящей: а) через начало	координат; б)	параллельно	прямой
4x − y − 2 = 0 ; в) перпендикулярно прямой 2x + 2y − 5 = 0

107

16. Составить уравнение касательной к кривой y = e− x , проходящей: а) параллельно биссектрисе второго и четвертого координатных углов; б) проходящей через точку (-1;0).


			7. Используя понятие дифференциала вычислить приближенно:
1.				2.			3.			4. 3			5. 3
		17				26			37			28		65
6.	7			7.	4		8.	4		9.4			10.	5
		126				82			260		627				33
11.				12.sin32o			13.		sin 47o	14.		cos 62o	15.	cos 48o
		3 245
16.		tg 46o		17.		tg 62o	18.		ctg 33o	19.		ctg 49o	20.e0,2
21.		e−0,1		22.		e0,3	23.		ln 1,1	24. ln 1,2			25. ln 0,9

	28.	arcctg
26. ln 0,8	27.arctg 1,05
	0,96

8.Используя формулу Тейлора, найти разложение заданных функций

вокрестности точки х=хо удерживая при этом n членов:

1. y = 2x3 + x2 −1; xo =1; n = 3

2. y = 3x3 − 4x2 + x; xo = 2; n = 3

3. y = 2x4 − x2 + x + 2; xo =1; n = 4

4. y = x5 − 3x2 + x; xo =1; n = 5

5. y = 3x4 − x2 + x + 2; xo = −1; n = 4

6. y = x3 + 2x2 + 4x +1; xo = −2; n = 3

y = e− x2

; xo = 0; n = 3

8. y = sin x2 ; xo

= 0; n = 2

y = ln(1+ 2x2 ); xo = 0; n = 2

10.

y = 1+ x4 ;

= 0; n = 2

y = arctgx; xo =1; n = 2

11.

y = 1+ 3x;

=1; n = 2

12.

y = arcsin x;

= 0; n = 2

13.

14.

y = 3 1+ 7x;

=1; n = 2

y = ln(x + 2x3 );

xo =1; n = 2

15.

y = 4 5+11x; xo =1; n = 2

16.

17.

y = cos(x2 );

= 0; n = 3

4.4. Неопределенный интеграл.

Таблица интегралов (C - произвольная постоянная).

108

1.∫xα dx = xα +1/(α +1) + C, α ≠ −1, α = const.

2.∫ dxx = 2x + C.

3.∫ dxx = ln | x | +C.

4.∫ex dx = ex + C, e ≈ 2.718281828.

5.∫ax dx = ax/lna + C, a = const, a ≠1, a > 0.

6.∫sin xdx = −cos x + C.

7.∫cos xdx = sin x + C.

8.∫ cos12 xdx = x + C.

9.∫ sin12 xdx = −x + C. 1 1 x

10.∫ x2 + a2 dx = a a + C =

=− 1 x + C1, a = const, a > 0. a a

1 1 | x − a |

11.∫ x2 − a2 dx = 2a ln | x + a | + C, a = const, a > 0.

12.	∫	1			dx = arcsin(x/a) + C =


		a2 − x	2
		a2 − x	2
		= −arccos(x/a) + C1, a = const, a > 0.
		1
13.	∫	1		dx = ln \| x + x2 + b \| +C, b = const.

		x2 + b
		x2 + b

Основные свойства неопределенного интеграла (C=const).

1.∫(u(x) ± v(x))dx = ∫u(x)dx ± ∫v(x)dx.

2.∫Cu(x)dx = C∫u(x)dx.

3.∫d( f (x)) = f (x) + C.

4.(∫u(x)dx)' = u(x).

5.d(∫u(x)dx)= u(x)dx.

Интегрирование по частям: ∫udv = uv − ∫vdu.

109


x = ϕ(t)
′	'	(t)dt.
Замена переменной: ∫u(x)dx = dx = ϕ (t)dt	= ∫u(ϕ(t))ϕ	(t)dt.

t = ϕ −1(x)

При нахождении интеграла часто помогают две формулы: формула изменения функции, стоящей под знаком дифференциала:

d[ f (x)] = 1 d[ f (x) k + m], k,m = const ; k

иформула внесения под знак дифференциала:

∫f (x) g(x)dx = (∫f (x)dx = F(x))= ∫g(x)d(F(x)).

Приведем примеры решения задач по нахождению неопределенных

интегралов.

В примерах 1-6 применяются свойства интегралов и описанные выше

две формулы.

1. ∫(8x +

−

)dx =∫8x dx + 5∫

dx − 3∫

dx=

x2 − 8

sin

x2 − 8

− 5ctgx − 3ln | x +

x2 − 8 | +C .

ln8

2. ∫(

− 5

− 9cos2x −

)dx =

+ 2

2x8

= −

∫x−8 / 5dx −

∫cos2xd(x 2) −

∫

dx =

+ (

2 /3)

=−

x−3/ 5

−

sin(2x) −

arctg

+ C .

5 2

− 3/5 2

3 2 /3

2 / 3

3. ∫7

dx =

∫(3x + 4)1/ 7 d(x 3+ 4)=[t = 3x + 4]=

∫t1/ 7dt =

t8 / 7

+ C =

3x + 4

3 8/ 7

7 (3x + 6)8 + C .

d(x (−8) + 3)

4. ∫

= −

∫

=[t = 3− 8x ]= −

∫

=−

2 t

+ C =

3− 8x

=−

3− 8x

+ C .

5. ∫cos x7(6sin x +1)2 dx =(∫cos xdx = sin x)= ∫(6sin x +1)2 / 7 d sin x =

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2011 12 13 14 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.01.2020119.81 Кб2Маркетинговые исследования.doc
#
04.03.2016111.23 Кб35маркина.docx
#
01.12.2019138.75 Кб3Массовые коммуникации.doc
#
04.01.20206.51 Mб0Математика в печать исправленная1.doc
#
04.03.2016620.54 Кб122Математика.doc
#
04.03.20163.05 Mб75МАТЕМАТИЧЕСКИЙ ПРАКТИКУМ.pdf
#
04.03.2016955.9 Кб30материал по социологии.doc
#
30.12.20194.93 Mб0материалы по цитологии.doc
#
15.12.2019301.21 Кб0матод ворд.doc
#
27.11.2019380.47 Кб9Матричные игры.docx
#
27.11.20192.39 Mб11МЕБЕЛЬ.doc