Формулирование задачи дп

Дано:множество состояний, в том числе начальные и конечные;множество возможных переходов из одного состояния в другое.

Найти:оптимальную последовательность переходов из начального состояния в конечное (максимальная или минимальная сумма чисел); предполагается, что хотя бы один путь существует.

Математическая модель:

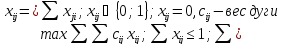
В.17Чтобы поставленная задачи оптимального планирования приобрела количественный математический характер, необходимо ввести в рассмотрение некоторый численный критерий W. Этот критерий будет характеризовать качества, успешность, эффективность операций.

В зависимости от характера решаемой задачи величина W может выбираться различными способами. Например, при планировании деятельности системы промышленного предприятия в качестве критерия W может быть выбран общий годовой объем продукции или же чистый годовой доход. Критерием эффективности работы транспортной системы может быть общий грузооборот.

При отыскании оптимального планирования операцииделятся на этапы. В связи с этим процесс планирования становится многошаговым и развивается от этапа к этапу. Каждый раз оптимизируется управление только на одном шаге.

Подходы:Нисходящее (задача разбивается на подзадачи меньшего размера, они решаются и затем комбинируются для решения исходной задачи). Восходящее (подзадачи, которые впоследствии понадобятся для решения исходной задачи просчитываются заранее и затем используются для построения решения исходной задачи).

• Задача распадается на m шагов. На каждом шаге определяется показатель эффективности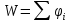i-шаги

В задачах ДП критерий эффективности называется выигрышным.

Шаговое управление – переменные, от которых зависят выигрыши на i-ом шаге и выигрыш в целом. Нужно учитывать возможные исходы предыдущего шага, влияние управления на все последующие исходы.

Управление процессом – последовательность шагов управления.

Оптимальное управление – значение управления, при котором оно является maxили min, и состоит из множества выигрышей на каждом шаге.

В.18Метод динамического программирования состоит в том, что оптимальное управление строится постепенно, шаг за шагом. На каждом шаге оптимизируется управление только этого шага. Вместе с тем на каждом шаге управление выбирается с учетом последствий, так как управление, оптимизирующее целевую функцию только для данного шага, может привести к неоптимальному эффекту всего процесса. Управление на каждом шаге должно быть оптимальным с точки зрения процесса в целом.

Управление на каждом шаге надо выбирать с учетом его последствий на предстоящих шагах. Это основное правило ДП, сформулированное Р. Беллманом, называется принципом оптимальности.

Оптимальное управление обладает таким свойством, что каково бы ни было начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться оптимальными относительно состояния, к которому придет система в конце данного шага.

В.19Приведем общую схему применения метода ДП.

Предположим, что все требования, предъявляемые к задаче динамического программирования, выполнены. Построение метода ДП для решения сводится к следующим моментам:

1) Выбирается способ деления процесса управления на шаги.

2) Определяются параметры состояния Sk и переменные управления Xk на каждом шаге.

3) Записываются уравнения состояний.

4) Вводятся целевые функции K-го шага и суммарная целевая функция.

5) Вводятся условные максимумы (минимумы) Z*K(Sk-1) и условное оптимальное управление на K-м шаге: X*K(Sk-1), K =N, N-1, …, 2, 1.

6) Решаются последовательно уравнения Беллмана (условная оптимизация).

7) После выполнения условной оптимизации определяется оптимальное решение для конкретного начального состояния S0:

А) Zmax = Z*1(s0) (здесьZmax = max Z)

Б) по цепочке

Оптимальное управление: Х* =(Х1*, Х2*, …, ХN*).

В.20 Задача набора высоты и скорости. Самолет (или др. летательный аппарат), находящийся на высоте H0 и имеющий скорость V0, должен быть поднят на заданную высоту Нкон и его скорость должна быть Vкон. Известен расход горючего, необходимый для подъема аппарата с высоты Н1 на высоту Н2 при постоянной скорости, известен расход горючего при увеличении скорости при неизменной высоте. Требуется найти оптимальный режим набора высоты и скорости, при котором общи расход горючего будет минимальным.

Решение:Разобьём процесс расхода высоты и скорости на этапы. На каждом этапе самолёт увеличивает только высоту или только скорость. Состояние самолета изображается в виде точки на некоторой плоскости VOH

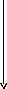
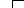
V

Vкон

V

V0

S0

S

Sкон

Нкон

Н

Н0

Критерий W – расход горючего. W->min

Найдем решение задачи с помощью метода динамического программирования. Высоту разделим на n1 равных частей.ΔH=(Hкон –H0)/n1; n1=6

Скорость, которую требуется набрать разделим на n2 частей.ΔV=(Vкон –V0)/n2; n2=8

В сумме n1 и n2 будут определять количество этапов. m=n1+n2 , m=8+6=14

Каждому из отрезков соответствует расход горючего в некоторых условных единицах.

Для решением методом Беллмана будем оптимизировать каждый шаг начиная с последнего. Т.о. переходя от точки к точке с права на лево и сверху вниз (от конца процесса к его началу) можно для каждой из точки выбрать условный минимум управления на следующем шаге. Т.е. направление, ведущее в Sкон с минимальным расходом горючего.

Чтобы найти из каждой точки оптимальный следующий шаг нужно проследить возможные пути из этой точки: вправо и вверх и для каждого пути найти сумму расходов на данном шаге и минимальный расход горючего на оптимальном положении. Из двух путей выбираем с наименьшим расходом горючего. Достигаем точки S0 и в результате получаем путь, указывающий движение из точки S0 в Sкон.

В.21Задача о распределении ресурсов.

Пусть n предприятий использует некоторые ресурсы. Известно что, если K–ому предприятию выделить X единиц ресурсов, то количество произведенной продукции будет равно φk(X). Требуется распределить A единиц ресурсов между всеми предприятиями так, чтобы выпуск продукции был максимальным.

Обозначим через Xk количество ресурсов, которое нужно выделить K-му предприятию, тогда математическая модель задачи запишется так: 

φ1(X1)+φ2(X2)+…+φn(Xn)→max 

при ограничениях X1+X2+…+Xn=A X1≥0, X2≥0,…,Xn≥0.

Если φ1, … φn – заданы таблично, то задача решается методами динамического программирования. 

Рассмотрим оптимальное распределение ресурсов с помощью метода динамического программирования. При решении задачи о распределении ресурсов введем функцию Беллмана fk(X) – максимальное количество продукции, которое могут выпустить K предприятий, при этом φk(X) – количество ресурса, получаемое K-ым предприятием при оптимальном распределении ресурса между первыми предприятиями. 

Предположим, что fk(X) известна, тогда вычислим fk+1 (X). Пусть К+1–ое предприятие получает t единиц (0 ≤ t ≤ X) ресурса, тогда оно выпускает φk+1(t) единиц продукции. На долю же первых K предприятий останется X–t единиц ресурса. 

В силу принципа оптимальности: чтобы получить больше продукции, необходимо распределить оптимально оставшиеся (X–t) единиц ресурса между K предприятиями. Тогда общий выпуск продукции будет равен φk+1(t)+fk(X–t). Но, чтобы этот общий выпуск продукции был максимальным, необходимо t подобрать так, чтобы эта сумма достигала наибольшего значения, т.е. fk+1(X).

Функциональное уравнение Беллмана:

В.22Задача о рюкзаке— одна из задач комбинаторной оптимизации. Название получила от максимизационной задачи укладки как можно большего числа нужных вещей в рюкзак при условии, что общий объём (или вес) всех предметов, способных поместиться в рюкзак, ограничен.

В общем виде: из неограниченного множества предметов со свойствами «стоимость» и «вес», требуется отобрать некое число предметов таким образом, чтобы получить максимальную суммарную стоимость при одновременном соблюдении ограничения на суммарный вес.

Разновидности: 1)Каждый предмет из множества можно выбирать произвольное количество раз.2)Каждый предмет можно использовать только один раз.

Задача о ранце с возможностью бесконечного выбора предметов

По данному набору из n предметов стоимостями  и весами  найти поднабор (с учетом того, что можно брать один предмет несколько раз) такой, что его стоимость будет максимальна среди всех поднаборов веса не более W.

Обозначим через  максимальную стоимость, которую мы можем набрать при весе не более w. Получаем следующее рекуррентное соотношение:

 = 0 (при весе не более нуля максимальная стоимость 0)

, где n — размер набора

Использовать рекурсию напрямую нельзя, так как появляется большое число перекрывающихся задач и время выполнения может стать экспоненциальным.