Задача 66.

Составить каноническое уравнение параболы, вершина которой лежит в начале координат и которая проходит через точку F(2;-4);ox- ось симметрии.

Ответ: .

Задача 67.

Составить уравнение геометрического места точек, одинаково удаленных от точки F(2;0)и от прямой .

Ответ: .

Задача 68.

Составить каноническое уравнение параболы, если ее фокус находится в точке пересечения прямой с осью0х.

Ответ: .

Задача 69.

На параболе найти точку, фокальный радиус которой равен 4.

Ответ: ,.

Задача 70.

Написать уравнение окружности, проходящей через начало координат и точки пересечения параболы с осями координат.

Ответ: .

Задача 71.

Написать уравнение параболы, если она проходит через точки пересечения прямой и окружностии симметрична относительно оси.

Ответ:.

Задача 72.

Как расположены на плоскости точки, координаты которых удовлетворяют условиям:

;.

Задача 73.

Какое геометрическое место точек определяется уравнением:

1. 

Ответ: Точка с координатами (-1, 3/2);

2. 

Ответ: ;

3. 

Ответ: ;

4. 

Ответ: ;

5. 

Ответ: .

Практическое занятие 7. Матрицы

Вопросы для повторения

1. Транспонирования матриц.

2. Операции сложения и вычитания матриц.

3. Операции умножения и возведения в степень матриц.

4. Понятие обратной матрицы.

Задача 74.

Найти сумму матриц:

,.

Решение:

.

Задача 75.

Даны три матрицы:

,,.

Найти матрицу .

Решение:

,,.

.

Задача 76.

Найти произведение матриц и:

1. ,;

2. ,;

3. ,.

Ответ:

1. ,;

2. ,;

3. ,.

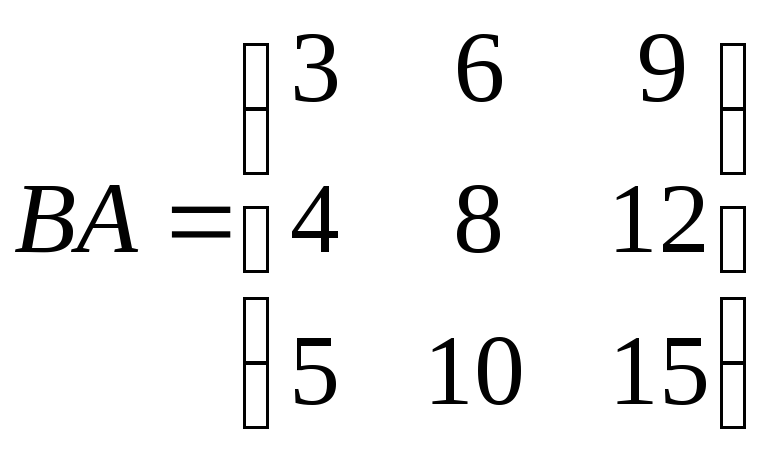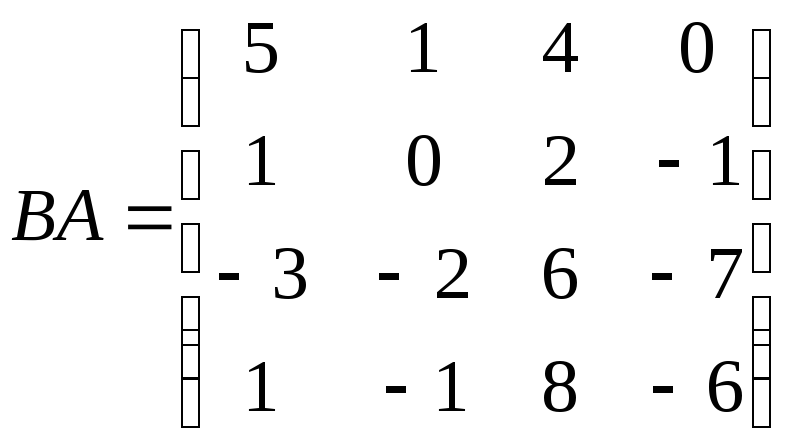Способ нахождения обратной матрицы

Пусть – невырожденная матрица. Припишем к ней справа (или слева) единичную матрицу. Далее с помощью элементарных преобразований над строками сдвоенной матрицылевая половина приводится к единичной матрице. Тогда сдвоенная матрица приобретает вид.

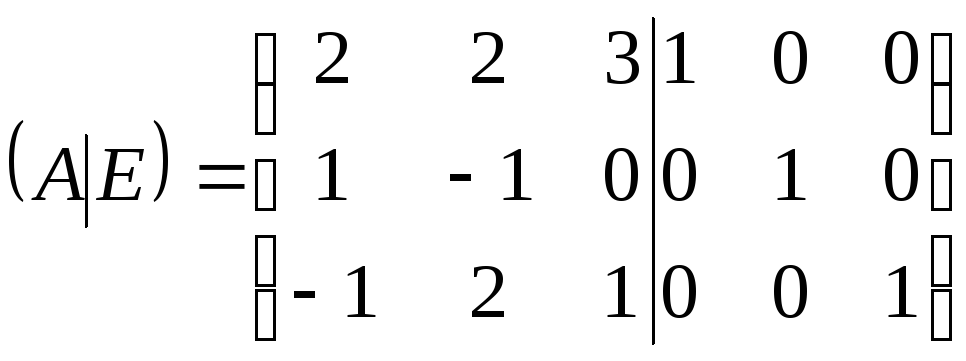
Задача 77.

Для матрицы найти обратную матрицуи проверить равенство.

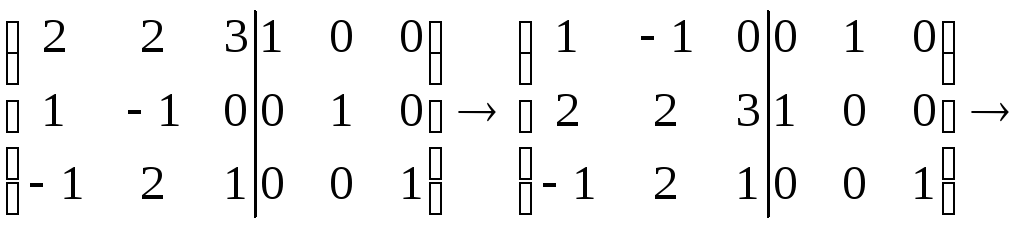
Решение:

При описанном выше способе нет необходимости специально проверять невырожденность матрицы . Это будет вытекать из самой возможности приведенияк.

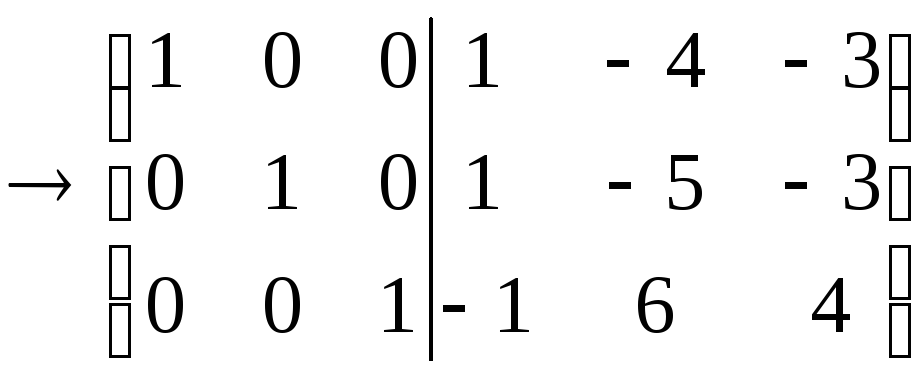
Практическое занятие 8. Определитель и ранг матрицы

Вопросы для повторения

1. Определитель - го порядка.

2. Свойства определителей.

3. Правила нахождения определителей - го порядка.

4. Понятие ранга матрицы.

Задача 78.

Упростить выражение: .

Решение:

Задача 79.

Решить уравнение: .

Решение:

.

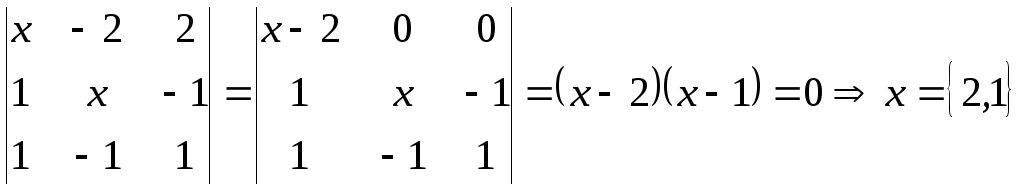Задача 80.

Вычислить определитель: .

Решение:

.

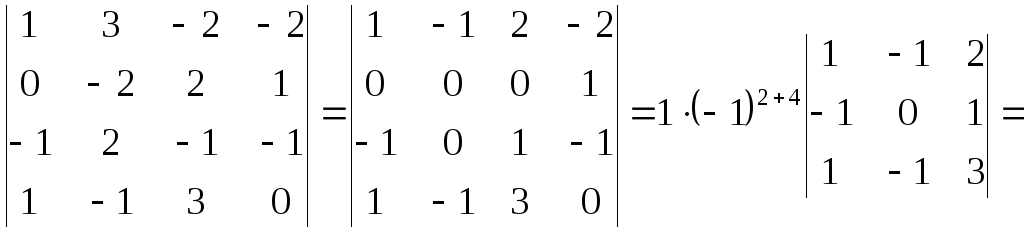
Задача 81.

Для данной матрицы 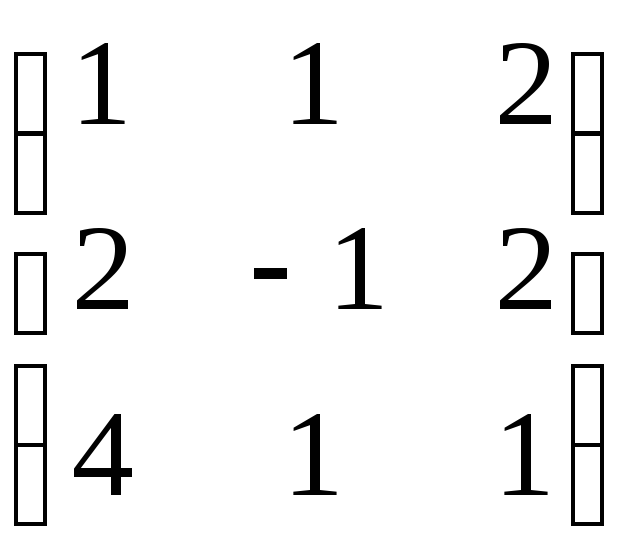найти обратную

1. методом исключения:

2. методом присоединенной матрицы.

Решение:

1. 

;

2. ; .

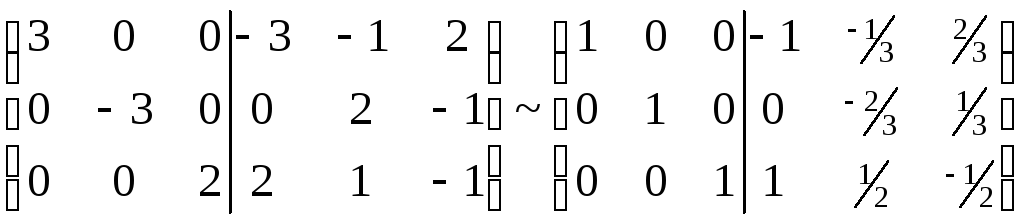Задача 82.

Решить матичное уравнение

1. методом исключения;

2. методом обратной матрицы.

Решение:

1. 

;

2. Введем обозначение , тогда уравнение запишется в виде. Умножив слева это уравнение на обратную матрицу, которая существует, поскольку.

.

Тогда .

Задача 83.

Вычислить определитель третьего порядка .

Решение:

Используя формулу Саррюса, получим:

.

Задача 84.

Найти ранг матрицы методом элементарных преобразований:

.

Решение:

Приведем матрицу к ступенчатому виду с помощью элементарных преобразований:

Полученная матрица содержит две ненулевые строки, значит, ее ранг равен 2. Следовательно, ранг исходной матрицы также равен 2.

Задача 85.

Найти ранг матрицы методом окаймляющих миноров и указать один из базисных миноров .

Решение:

Так как у матрицы Aесть ненулевые элементы, то. Найдем какой-либо ненулевой минор 2-го порядка (если он существует). Таким минором является, например.

Значит, . Вычислим миноры третьего порядка, окаймляющие:

;

Все миноры 3-го порядка, окаймляющие , равны нулю, следовательно. Итак,.

Одним из базисных миноров является .

Практическое занятие 9. Многочлены

Вопросы для повторения

1. Сложение и умножение многочленов.

2. Теорема о делении с остатком.

3. Понятие корня многочлена.

4. Понятие кратности корня многочлена.

5. Схема Горнера.

6. Соотношение степени многочлена и числа его корней.

7. Разложение правильной рациональной дроби на простейшие.

8. Метод неопределенных коэффициентов.

Задача 86.

Выполнить деление с остатком на.

Решение:

Задача 87.

на.

Решение:

Задача 88.

на.

Ответ: (Частное, остаток).

Задача 89.

на.

Ответ: .

Задача 90.

При каком условии полином делится на полином.

Ответ: .

Задача 91.

При каком условии полином делится на полином.

Ответ:

Если , то; если, то.

Схема Горнера

Пусть _.

Если , то коэффициенты многочленаипроще всего найти по схеме Горнера.

Задача 92.

Пользуясь схемой Горнера вычислить _.

,.

Ответ:

	1	-3	6	-10	16
4	1	1	10	30	136

.

Задача 93.

Пользуясь схемой Горнера вычислить .

,.

Ответ:

	1	2	-3	-4	1
-1	1	1	-4	0	1

.

Задача 94.

Пользуясь схемой Горнера вычислить

,.

Ответ:

	1	-8	24	-50	90
2	1	-4	8	-18	18

.

Задача 95.

Пользуясь схемой Горнера вычислить

,.

Ответ:

	1	0	0	0	0	0
1	1	1	1	1	1	1

.

Задача 96.

Разложить на простейшие дроби .

Ответ: .

Задача 97.

Разложить на простейшие дроби .

Ответ: .

Задача 98.

Разложить на простейшие дроби .

Ответ: .

Задача 99.

Разложить на простейшие дроби (не вычисляя коэффициентов) .

Ответ:

.

Задача 100.

Разложить на простейшие дроби (не вычисляя коэффициентов) .

Ответ: .

Практическое занятие 10. Квадратичные формы

Вопросы для повторения

1. Построение матрицы квадратичной формы.

2. Канонический базис квадратичной формы и приведение квадратичной формы к каноническому виду.

3. Канонический базис Якоби.

4. Критерий Сильвестра знакоопределенности квадратичной формы.

Задача 101.

Записать матрицу для квадратичной формы:

1. 

Ответ: ;

2. 

Ответ: .

Задача 102.

Записать квадратичную форму для матриц

.

Задача 103.

Исследовать на знакоопределенность квадратичные формы:

1. 

Ответ: знаконеопределена;

2. 

Ответ: знаконеопределена;

3. 

Ответ: знаконеопределена;

4. 

Ответ: положительноопределена;

5. 

Ответ: знаконеопределена.

Задача 104.

Найти все значения параметра , при которых положительно определены следующие квадратичные формы:

1. 

Ответ: ;

2. 

Ответ: ;

3. 

Ответ: Не существует.

Задача 105.

Найти все значения параметра , при которых отрицательно определены следующие квадратичные формы:

1. 

Ответ: Не существует;

2. 

Ответ: ;

3. 

Ответ: .

Задача 106.

Привести к каноническому виду квадратичные формы:

1. ;

2. ;

3. .

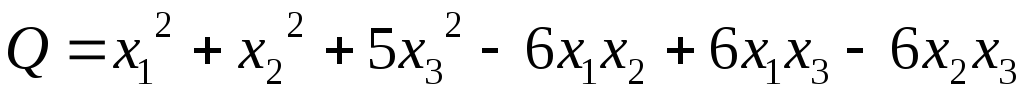Практическое занятие 11. Системы линейных уравнений

Вопросы для повторения

1. Критерий Кронекера-Капелли.

2. Совместные и определенные системы линейных уравнений.

3. Методы решения систем линейных уравнений и условия их применимости.

Задача 107.

Методом Гаусса решить систему .

Решение: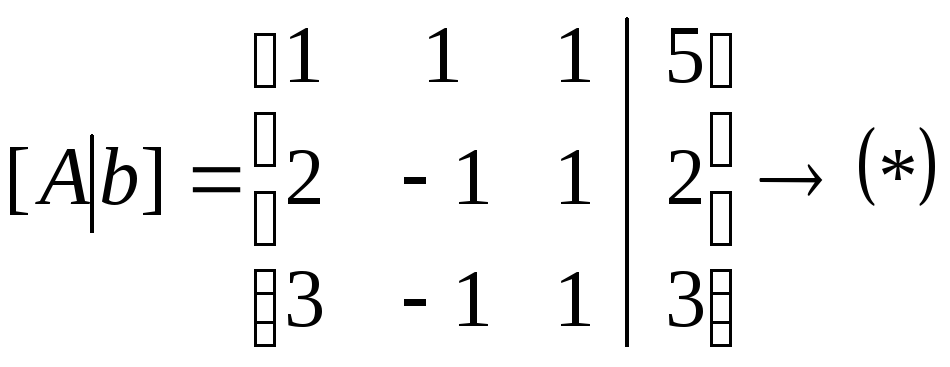

Ко второй строке прибавим первую, умноженную на , а к третьей – первую, умноженную на. Получим:

Ко второй строке прибавим третью, умноженную на .

К третьей строке прибавим вторую, умноженную на .

.

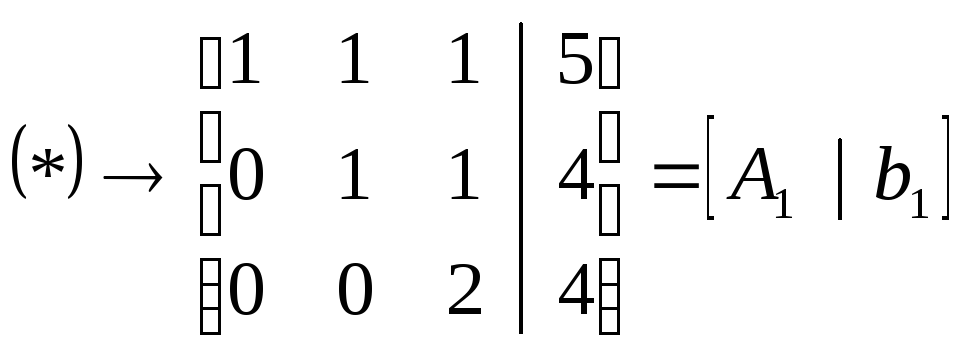Этой матрице соответствует система:

.

Ответ:

Задача 108.

Решить систему .

Решение:Решаем систему методом Гаусса:

.

Ко второй строке прибавим первую, умноженную на , а к третьей – первую, умноженную на:

.

К третьей строке прибавим вторую, умноженную на .

.

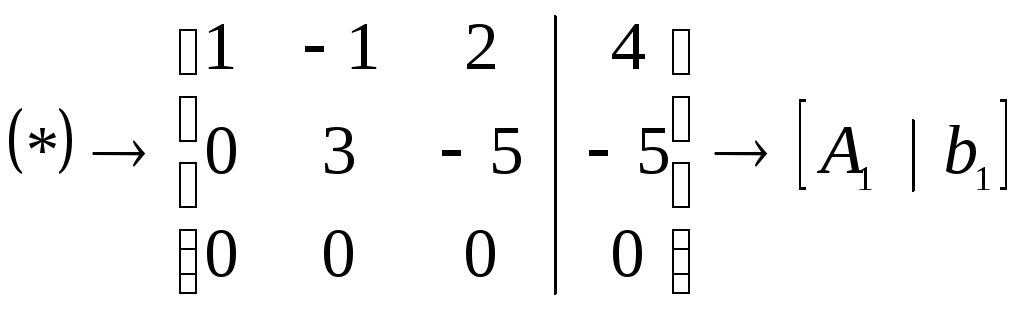Этой матрице соответствует система

.

Получаем формулы для вычисления решений системы линейных уравнений

гдеc- любое число.

Таким образом, система имеет бесконечное множество решений. Получать решения можно, подставляя вместо cконкретные числовые значения. Например,

;.

Задача 109.

Решить систему линейных уравнений .

Решение: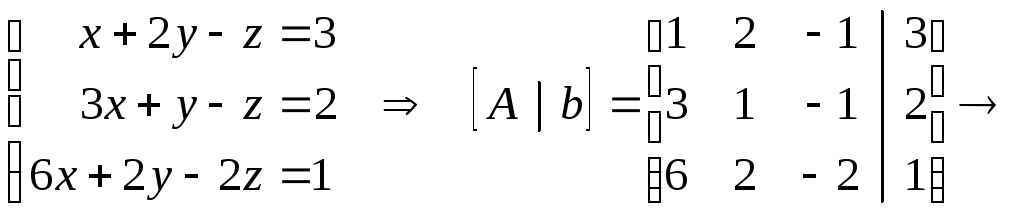

.

Соответствующая система не имеет решений. Значит и исходная система несовместна.

Решение задач линейной алгебры и линейного программирования в таблицахExcel

Практическое занятие 1. Простейшие операции над матрицами в Excel

При выполнении операций над матрицами в Excel необходимо соблюдать следующий порядок команд:

1. Выделение области ячеек, где будет записан ответ;

2. Операции начинаются со знака равенства (<=>), даже при вводе формул;

3. Вводимые данные, т.е. матрицы, с которыми производятся операции, выделяются как блок (диапазон) ячеек;

4. Операции сложения, вычитания, умножения матрицы на число производятся с помощью аналогичных команд с клавиатуры или мыши, а остальные - умножение матрицы на матрицу, транспонирование, обращение и т.д. - с помощью матричных функций;

5. Заканчивать ввод нужно не нажатием клавиши <Enter>, а комбинацией клавиш <Shift>+<Ctrl>+<Enter>. Для правильного ввода данной команды необходимо при нажатых клавишах <Shift>+<Ctrl> нажать клавишу <Enter>.