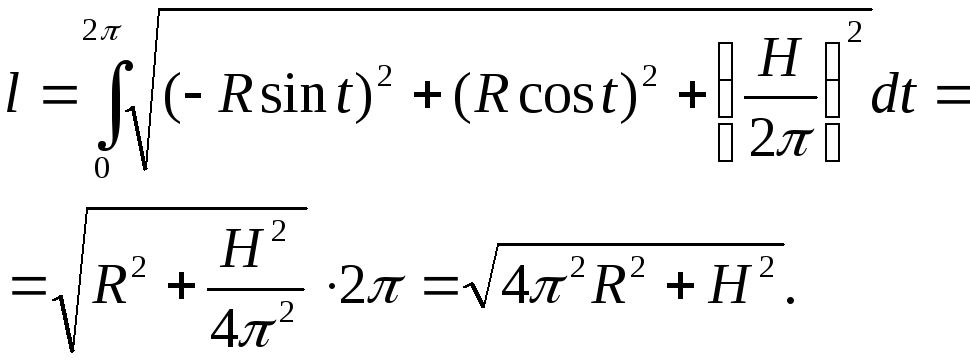I Определение понятия длины кривой

Рассмотрим плоскую линию АВ, заданную параметрическими уравнениями где и– непре-рывные функции. Такую кривую называют простой, если различным значениям параметра соответствуют различные точки кривой, за исключением значенийи, которым может соответствовать одна точка в случае замкнутой кривой. Простой линией является, например, график функции.

Разобьем эту линию точками наn частей и соединим соседние точки отрезками прямых. Получим n-звенную ломанную, вписанную в линию АВ. Длину k-го звена ломанной обозначим (это расстояние между точкамии). Длину наибольшего звена обозначим. Периметр ломанной:.

Определение. Если при существует конечный предел, то:1) линиюАВ называют спрямляемой; 2) число l называют длиной линии.

II Явное задание линии

Теорема 1. Пусть АВ – это график непрерывно-дифференцируемой функции . Такая линия спрямляема и её длина вычисляется по формуле

(1)

Доказательство. Для определенности считаем, что точка А имеет координаты , а точкаВ – . Обозначим черезкоординаты точки, так что абсциссы этих точек дают разбиение отрезка[a,b]: . Длинаk-го звена ломанной

Как обычно обозначим , а к приращению функции применим теорему Лагранжа:

.

Следовательно,

.

Длина всей ломанной

представляет собой интегральную сумму для функции . Kроме того, условие равносильно. В силу условий теоремы функцияF(x) непрерывна, следовательно, интегрируема. Поэтому , т.е. длина линииАВ, есть не

что иное, как интеграл в правой части формулы (1). Теорема доказана.

Пример 1. Вычислить длину части полукубической параболы , расположенной внутри параболы.

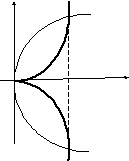
Решение. Находим точки пересечения линий:

(корень – посторонний, ибо линии распо-

х ложены в правой полуплоскости). Уравнения

линий не изменяются при замене y на (– y). Это

означает симметрию относительно оси Ox.

Поэтому достаточно вычислить длину части ли-

линии, лежащей в 1-й четверти. Здесь полукуби-

ческая парабола – это график функции

.

Подготовительные вычисления

Итак, искомая длина:

.

Замечание 1. Если линия АВ задана явным уравнением то её длина выражается формулой

III Параметрическое задание линии

Теорема 2. Пусть простая линия АВ задана параметрическими уравнениями

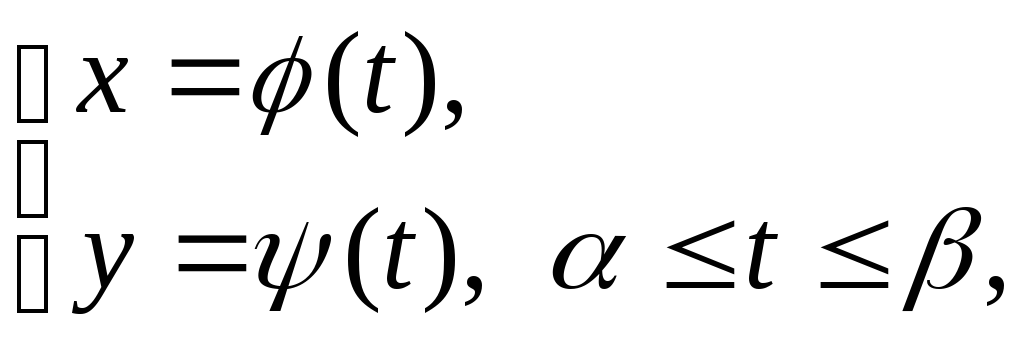
причем функции и– непрерывно-дифференцируемы. Тогда линия спрямляема и ее длину можно вычислить по формуле

(2)

Доказательство. Обозначим абсциссы крайних точек линии и пусть. Для упрощения доказательства будем считать, чтона, а следовательно (в силу непрерывности) сохраняет знак. Условиеозначает возрастание функции. Значити . В формуле (1) сделаем замену переменной . Тогда и и формула (1) принимает вид

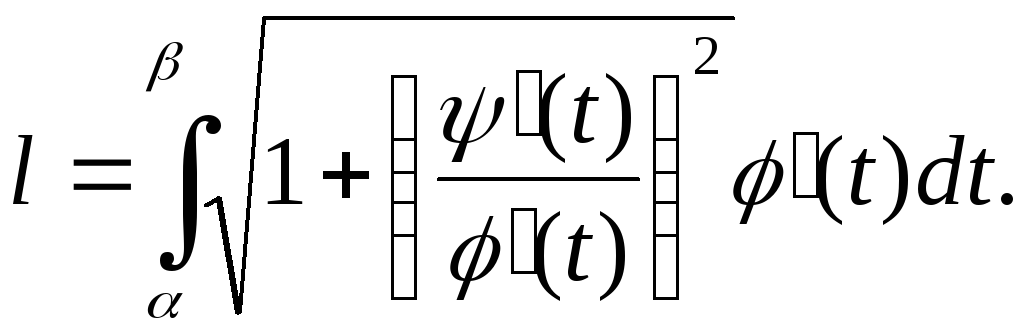
Элементарные преобразования приводят нас к формуле (2).

Если же , то убывает на и. Та же замена приведет нас к соотношению

Изменение направления интегрирования (от до) снова приведет нас к формуле (2). Теорема доказана.

Заметим, что есть доказательства формулы (2), не использующие условие знакопостоянства . Но они очень громоздкие и используют такие свойства непрерывных функций, которые находятся за пределами нашей программы.

Пример 2. Вычислить длину одной арки циклоиды

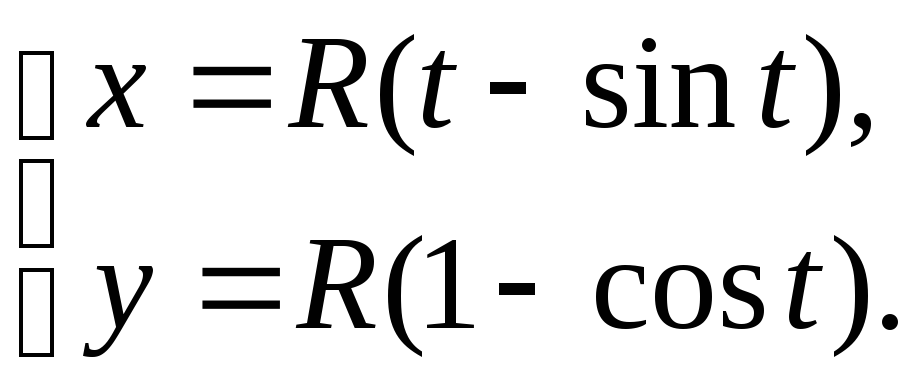
Циклоида – это плоская кривая, которую описывает фиксированная точка окружности радиуса R, катящаяся без скольжения по прямой линии.

Решение. Первая арка циклоиды соответствует изменению параметра от 0 до . Вычислим производныеии найдем сумму их квадратов:

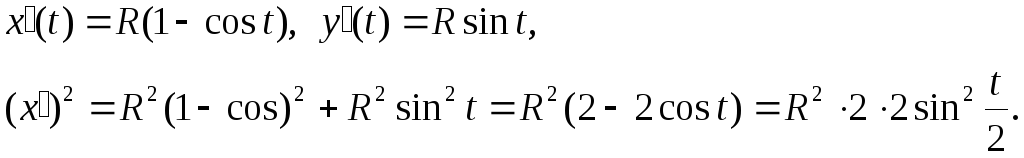
Заметим, что , ибо. Имеем для искомой длины:

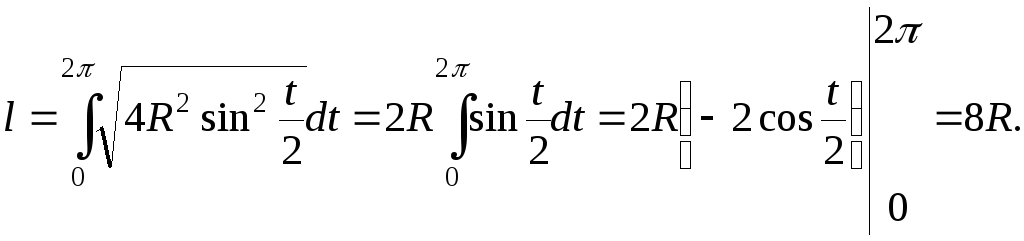
Замечание 2. Формула (2) естественным образом обобщается на случай пространственных линий :

Пример 3. Найти длину одного витка винтовой линии

Решение. Первый виток соответствует изменению параметра от 0 до . Имеем для длины: