III Вычисление объёмов тел вращения

Определение 3. Тело вращения – это тело, полученное вращением плоской фигуры вокруг оси, не пересекающей фигуру и лежащей с ней в одной плоскости.

Ось вращения может и пересекать фигуру, если это ось симметрии фигуры.

Теорема 2. Пусть криволинейная трапеция, ограниченная графиком непрерывной неотрицательной функции , осьюи отрезками прямыхивращается вокруг оси. Тогда объём получающегося тела вращения можно вычислить по формуле

(2)

Доказательство. Для такого тела сечение с абсциссой – это круг радиуса, значити формула (1) даёт требуемый результат.

Если фигура ограничена графиками двух непрерывных функций и, и отрезками прямыхи, причёми, то при вращении вокруг оси абсцисс получим тело, объём которого

Пример 3. Вычислить объём тора, полученного вращением круга, ограниченного окружностью вокруг оси абсцисс.

Решение. Указанный круг снизу ограничен графиком функции , а сверху –. Разность квадратов этих функций:

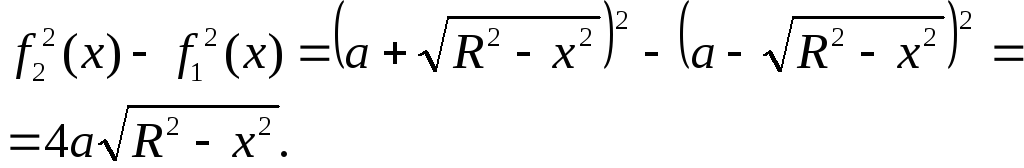
Искомый объём

(графиком подынтегральной функции является верхняя полуокружность, поэтому написанный выше интеграл – это площадь полукруга).

Пример 4. Параболический сегмент с основанием , и высотой, вращается вокруг основания. Вычислить объём получающегося тела («лимон» Кавальери).

Р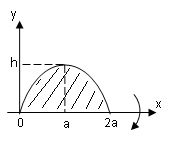ешение. Параболу расположим как показано на рисунке. Тогда её уравнение , причем. Найдём значение параметра:. Итак, искомый объём:

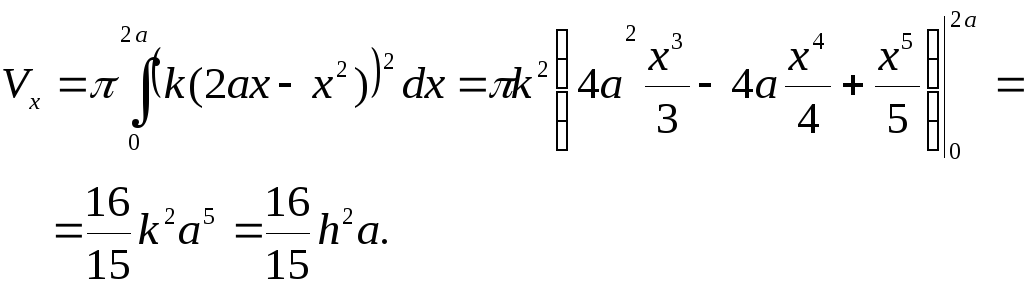
Теорема 3. Пусть криволинейная трапеция, ограниченная графиком непрерывной неотрицательной функции , осьюи отрезками прямыхи, причём, вращается вокруг оси. Тогда объём получающегося тела вращения может быть найден по формуле

(3)

Идея доказательства. Разбиваем отрезок точками, на части и проводим прямые. Вся трапеция разложится на полоски, которые можно считать приближенно прямоугольниками с основаниеми высотой.

Получающийся при вращении такого прямоугольника цилиндр разрежем по образующей и развернём. Получим «почти» параллелепипед с размерами: ,и. Его объём. Итак, для объёма тела вращения будем иметь приближенноё равенство

Для получения точного равенства надо перейти к пределу при . Написанная выше сумма есть интегральная сумма для функции , следовательно, в пределе получим интеграл из формулы (3). Теорема доказана.

Замечание 1. В теоремах 2 и 3 условие можно опустить: формула (2) вообще нечувствительна к знаку, а в формуле (3) достаточнозаменить на.

Пример 5. Параболический сегмент (основание , высота) вращается вокруг высоты. Найти объём получающегося тела.

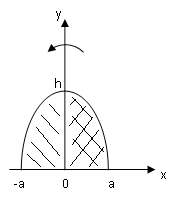Решение. Расположим параболу как показано на рисунке. И хотя ось вращения пересекает фигуру, она – ось – является осью симметрии. Поэтому надо рассматривать лишь правую половину сегмента. Уравнение параболы , причем, значит. Имеем для объёма:

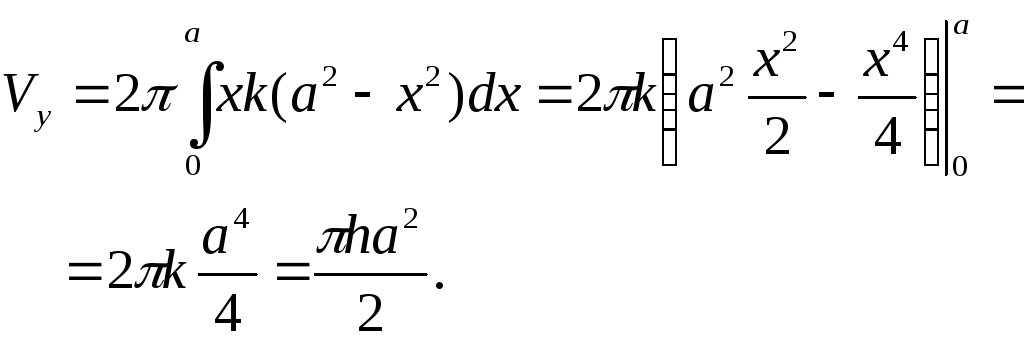
Замечание 2. Если криволинейная граница криволинейной трапеции задана параметрическими уравнениями ,,и,то можно использовать формулы (2) и (3) с заменойнаинапри измененииt от до.

Пример 6. Фигура ограничена первой аркой циклоиды ,,, и осью абсцисс. Найти объём тела, полученного вращением этой фигуры вокруг: 1) оси; 2) оси.

Решение. 1) Общая формула В нашем случае:

2) Общая формула Для нашей фигуры:

Предлагаем студентам самостоятельно провести все вычисления.

Замечание 3. Пусть криволинейный сектор, ограниченный непре-рывной линией и лучами,, вращается вокруг полярной оси. Объём получающегося тела можно вычислить по формуле.

Пример 7. Часть фигуры, ограниченной кардиоидой , лежащая вне окружности, вращается вокруг полярной оси. Найти объём тела, которое при этом получается.

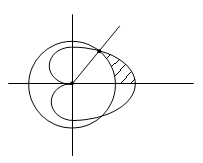Решение. Обе линии, а значит и фигура, которую они ограничивают, симметричны относительно полярной оси. Поэтому необходимо рассматривать лишь ту часть, для которой . Кривые пересекаются прии

при . Далее, фигуру можно рассматривать как разность двух секторов, а значит и объём вычислять как разность двух интегралов. Имеем:

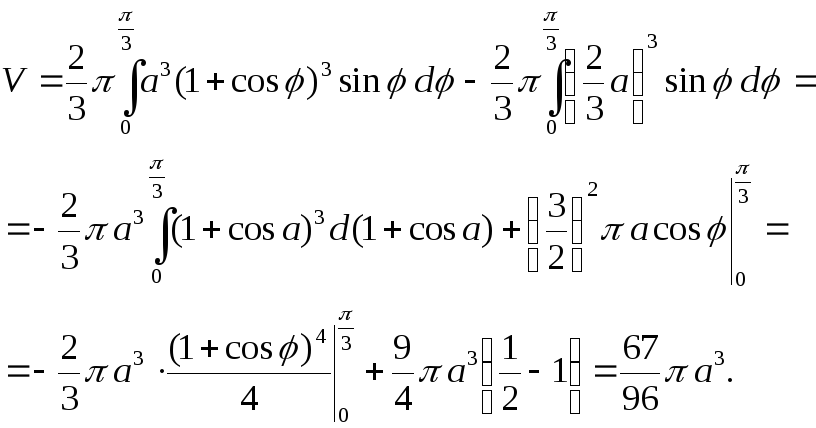
Задачи для самостоятельного решения.

1. Круговой сегмент, основание которого , высота , вращается вокруг основания. Найти объём тела вращения.

2. Найти объём параболоида вращения, основание которого , а высота равна.

3. Фигура, ограниченная астроидой ,вращает-ся вокруг оси абсцисс. Найти объём тела, которое получается при этом.

4. Фигура, ограниченная линиями ивращается вокруг оси абсцисс. Найти объём тела вращения.