- •Тема приложения определенного интеграла
- •§1. Понятие площади плоской фигуры
- •§2. Вычисление площадей плоских фигур
- •I Декартова система координат
- •II Полярная система координат
- •§3. Вычисление длин линий
- •I Определение понятия длины кривой
- •II Явное задание линии
- •III Параметрическое задание линии
- •IV Полярные уравнения линии
- •§4. Вычисление объёмов некоторых тел
- •I Понятие объёма тела. Объём цилиндра
- •II Вычисление объёма тела по его поперечным сечениям
- •III Вычисление объёмов тел вращения
- •§5. Вычисление площадей поверхностей вращения
- •I Определения
- •II Общая формула
- •1) 2) 3)
- •III Частные случаи и примеры
- •§6. Теоремы Паппа-Гульдина
II Полярная система координат
В полярной системе координат базовой фигурой является не криволинейная трапеция, а криволинейный сектор.
Определение.
Криволинейным сектором называют плоскую
фигуру, ограниченную непрерывной линией
![]() и двумя лучами
и двумя лучами![]() и
и![]() ,
где
,
где![]() .
.
Теорема 4. Криволинейный сектор является квадрируемой фигурой. Его площадь определяется формулой:
![]() (4)
(4)
Доказательство.
Разобьём отрезок
![]() точками
точками![]() и для каждого частичного отрезка
и для каждого частичного отрезка![]() построим круговые секторы, радиусы
которых равны наименьшему
построим круговые секторы, радиусы
которых равны наименьшему![]() и наибольшему
и наибольшему![]() значениям функции
значениям функции![]() на
на![]() .
.
При этом
![]() и
и![]() ,
где
,
где![]() (в силу непрерывности функции
(в силу непрерывности функции![]() ).
Получим две веерообразные фигуры, первая
из которых вписана в криволинейный
сектор, а вторая описана. Площади этих
фигур равны соответственно:
).
Получим две веерообразные фигуры, первая
из которых вписана в криволинейный
сектор, а вторая описана. Площади этих
фигур равны соответственно:
![]()
![]() ;
;
![]() .
.
В этих суммах
нетрудно увидеть интегральные суммы
для интегрируемой функции
![]() .
Следовательно, они имеют общий предел,
равный интегралу из формулы (4),
что и доказывает
эту формулу.
.
Следовательно, они имеют общий предел,
равный интегралу из формулы (4),
что и доказывает
эту формулу.
Пример 6.
Вычислить площадь фигуры ограниченной
полярной осью
![]() и первым витком спирали Архимеда
и первым витком спирали Архимеда![]()
Решение.
Первый виток спирали
![]() соответствует изменению угла
соответствует изменению угла![]() от 0 до
от 0 до![]() :
: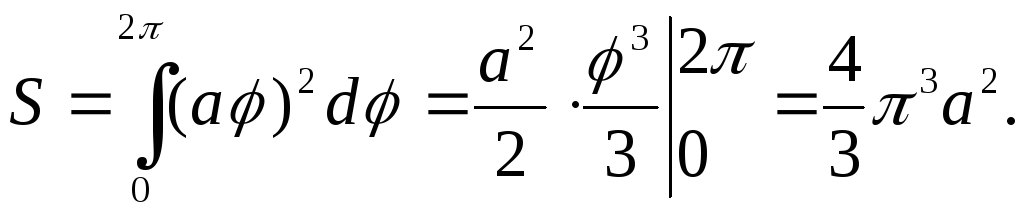
Теорема 5.
Если фигура ограничена двумя непрерывными
линиями
![]() и
и![]() и двумя лучами
и двумя лучами![]() ,
причём
,
причём![]() и
и![]() ,
то она является квадрируемой и её площадь
вычисляется по формуле:
,
то она является квадрируемой и её площадь
вычисляется по формуле:
![]() (5)
(5)
Доказательство.
Описанную в теореме фигуру можно
представлять как р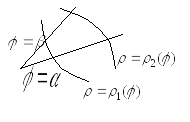 азность
двух криволинейных секторов. Записав
площадь каждого из них по формуле (4),
а затем,
используя свойство линейности
определён-ного интеграла, получим
требуемую формулу (5).
азность
двух криволинейных секторов. Записав
площадь каждого из них по формуле (4),
а затем,
используя свойство линейности
определён-ного интеграла, получим
требуемую формулу (5).
Пример 7.
Вычислить площадь части фигуры,
ограниченной линией
![]() ,
лежащей вне окружности
,
лежащей вне окружности![]() .
.
![]()
Р ешение.
Лемниската (как и окружность) симметрична
относительно осей координат, т.к.
пере-менные
ешение.
Лемниската (как и окружность) симметрична
относительно осей координат, т.к.
пере-менные
![]() и
и![]() входят в урав-нение лишь в чётных
степенях. Достаточно рассматривать
линии и фигуру, которую они ограничивают,
только в пер-вой четверти. Перейдём в
полярную систему координат и получим
полярные уравнения линий, использую
известные формулы, связывающие декартовые
и полярные координаты:
входят в урав-нение лишь в чётных
степенях. Достаточно рассматривать
линии и фигуру, которую они ограничивают,
только в пер-вой четверти. Перейдём в
полярную систему координат и получим
полярные уравнения линий, использую
известные формулы, связывающие декартовые
и полярные координаты:

Уравнение лемнискаты:
![]()
Окончательно,
![]() –
полярное уравнение лемнискаты. Уравне-ние
окружности ,
–
полярное уравнение лемнискаты. Уравне-ние
окружности ,![]() .
Лемниската существует для тех
.
Лемниската существует для тех![]() ,
для которых
,
для которых![]() .
В первой четверти – это сектор
.
В первой четверти – это сектор![]() .
.
Найдем точки
пересечения линий, для этого приравниваем
правые части уравнений:
![]() В первой четверти это уравнение имеет
единственный корень
В первой четверти это уравнение имеет
единственный корень![]() .
Далее, максимальное удаление точки от
полюса равноа
(при
.
Далее, максимальное удаление точки от
полюса равноа
(при
![]() ).
Точки же окружности находятся ближе к
полюсу. Итак, окончательно часть фигуры
в первой четверти ограничена лучами
).
Точки же окружности находятся ближе к
полюсу. Итак, окончательно часть фигуры
в первой четверти ограничена лучами![]() и
и![]() ,
и линиями
,
и линиями![]() (ближняя к полюсу граница) и
(ближняя к полюсу граница) и![]() (дальняя граница). Искомая площадь:
(дальняя граница). Искомая площадь:
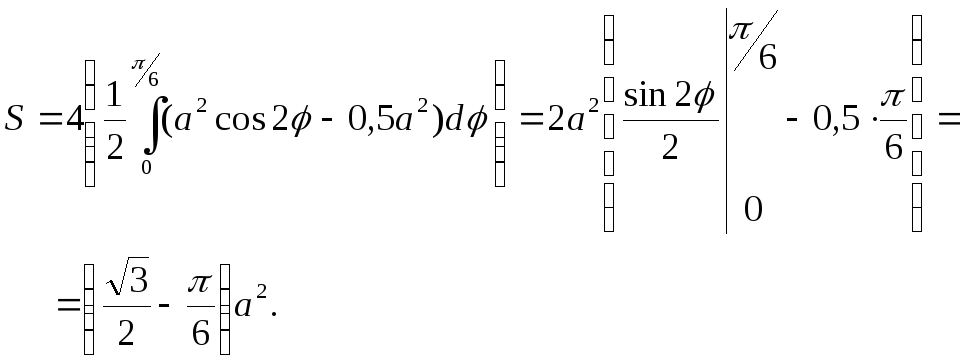
Задачи (для самостоятельного решения).
1. Найти площадь фигуры, которая ограничена замкнутой линией
![]() .
.
2. Найти прямую y=kx, которая разбивает параболический сегмент, ограни-
ченный линиями
![]() и
и![]() ,
на две равновеликие части.
,
на две равновеликие части.
3. Найти площадь
фигуры, ограниченной петлей линии
![]() .
.
4. Какую часть
площади круга
![]() составляет площадьn-лепестковой
составляет площадьn-лепестковой
розы
![]() ?
?
5.* Найти площадь фигуры, ограниченной замкнутой линией