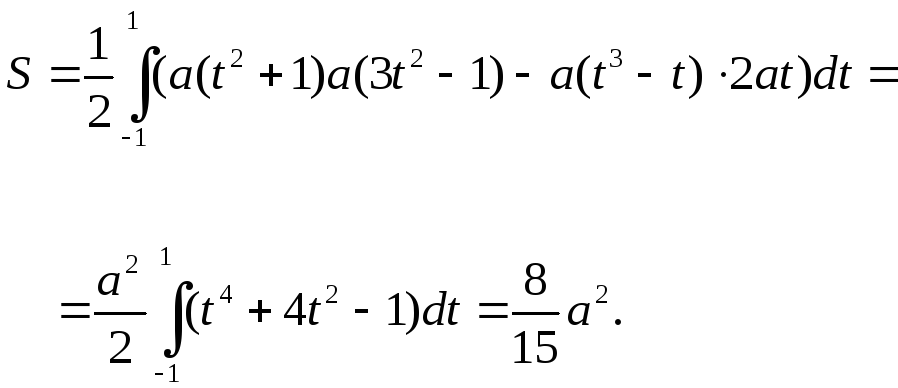–95–

Тема приложения определенного интеграла

§1. Понятие площади плоской фигуры

Площадь плоской фигуры – это числовая характеристика фигуры, которая обладает такими свойствами (– фигура, – её площадь):

1) 2), еслине имеют общих внутренних точек; 3) площадь квадрата со сторонойа равна . Эти свойства можно считать аксиомами площади. Второе свойство называется аддитивностью и из него вытекает ещё одно: – часть фигуры имеет площадь, меньшую, чем вся фигура.

В элементарной геометрии исходя из формул для площади квадрата последовательно выводят формулы для площади прямоугольника, парал-лелограмма, треугольника и произвольного многоугольника. В этом параграфе мы введём понятие площади произвольной плоской фигуры.

Будем говорить, что многоугольник вписан в фигуру, если каждая точка этого многоугольника принадлежит фигуреили её границе; если же все точки фигуры и её границы принадлежат некоторому многоугольнику, то будем говорить, что многоугольник описан вокруг фигуры:

Определение. Пусть для данной фигуры существует две последовательности многоугольниковитаких что,Еслито:

1) фигуру называют квадрируемой;

2) число называют площадью фигуры.

Можно доказать, что это определение корректно в следующем смысле: если кроме последовательностей многоугольников из этого определения существуют другие последовательности итакие, чтои, то обязательно.

Замечание. Вместо многоугольников можно использовать и другие фигуры, квадрируемость которых уже установлена.

§2. Вычисление площадей плоских фигур

I Декартова система координат

Теорема 1. Криволинейная трапеция, ограниченная графиком непрерывной неотрицательной функции , прямымии осью абсцисс, является квадрируемой фигурой. Её площадь выражается определённым интегралом:

(1)

Доказательство. Как и в §1 предыдущей темы разбиваем данный отрезок [a,b] на n частичных отрезков , Обозначим и, соответственно, наименьшее и наибольшее значения функциина отрезке .

у у

0 х 0 x

Так как функция непрерывна, а отрезок замкнут, то эти значения достигаются в некоторых точках:

На каждом частичном отрезке как на основании построим два прямоугольника: один c высотой , второй с высотой . Получим две ступенчатые фигуры: одна будет вписанa в криволинейную трапецию, вторая описана вокруг трапеции. Площади этих фигур( много-угольников!) имеют вид:

.

Но эти суммы являются интегральными суммами для интегрируемой ( в силу непрерывности) функции, следовательно, имеют своим общим пределом определённый интеграл. Таким образом, криволинейная трапеция является квадрируемой и имеет место формула (1). Теорема доказана.

Формула (1) – базовая, все другие формулы можно получить из неё.

Теорема 2. Пусть фигура ограничена графиками двух непрерывных функций и, и прямыми, причем. Тогда площадь фигуры можно вычислить по формуле:

(2)

y=g(x)

y=f(x)

а b x

Доказательство. Если оба графика выше оси (см.рисунок), то фигуру можно понимать как разность двух криволинейных трапеций, а её площадь – как разность двух интегралов. Применение свойства линейности интеграла даёт формулу (2).

Рассмотрим теперь общий случай произвольного расположения графиков относительно оси абсцисс. Так как функции ограничены (они непрерывны на замкнутом промежутке), то существует такое число , чтои. Значит ,

Нетрудно заметить, что этот интеграл равен интегралу из формулы (2).

Замечание 1. Если условие ,, нарушается, то отрезок – разбивают на части, где либо, либо. После этого используют аддитивность интеграла.

Замечание 2. В формулировках теорем говорится о прямых и. На самом деле речь идёт об отрезках этих прямых, которые, к тому же, могут вырождаться в точки.

Пример1. Найти площадь фигуры, ограниченной данными линиями

Р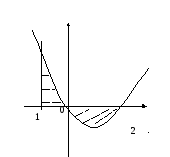ешение. Находим точки пересечения графиков двух функций:

Точка разделяет отрезокна две части, где графики расположены по-разному. Имеем для площади:

Пример 2. Найти площадь фигуры, ограниченной линиями

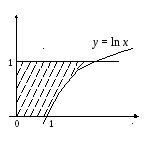
Решение. На фигуру удобно смотреть как на трапецию, примыкающую к оси : фигура ограничена графиком функции(равносильна), прямымии(осью). Нетрудно написать соответству-ющую формулу и вычислить площадь:

Теорема 3. Пусть криволинейная трапеция ограничена прямыми и, осью абсцисс и линией, заданной параметрическими уравнениями:

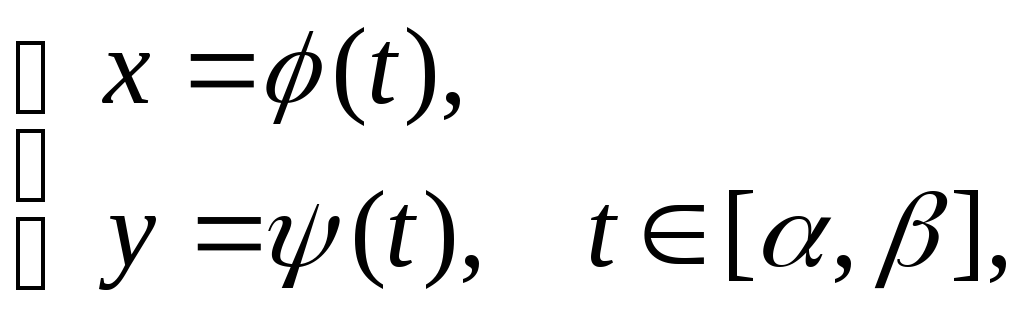
причём ,и. Тогда площадь такой фигуры вычисляется по формуле:

(3)

Эта теорема есть прямое следствие теоремы о замене переменной в определённом интеграле.

Пример 3. Вычислить площадь фигуры ограниченной эллипсом:

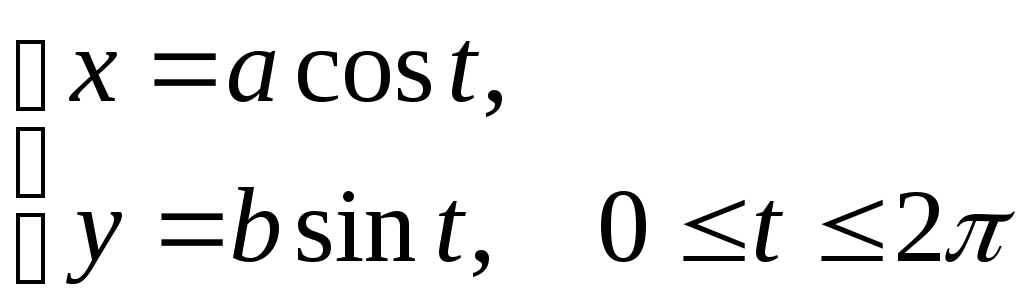
Решение. Эллипс симметричен относительно осей координат, поэтому достаточно вычислить площадь только той части фигуры, которая находится в I четверти.

Заметим, что, и, и:

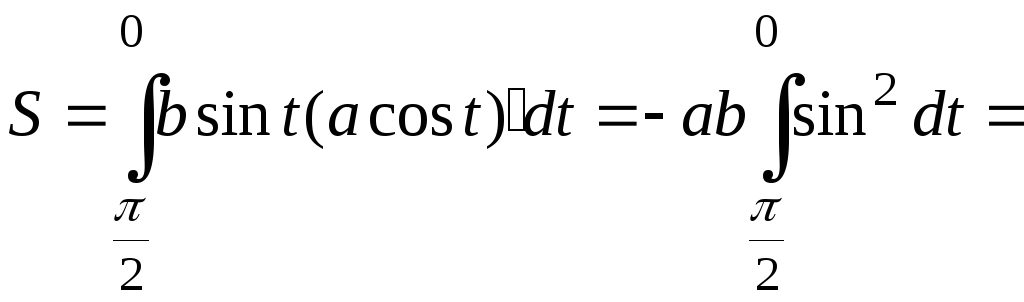
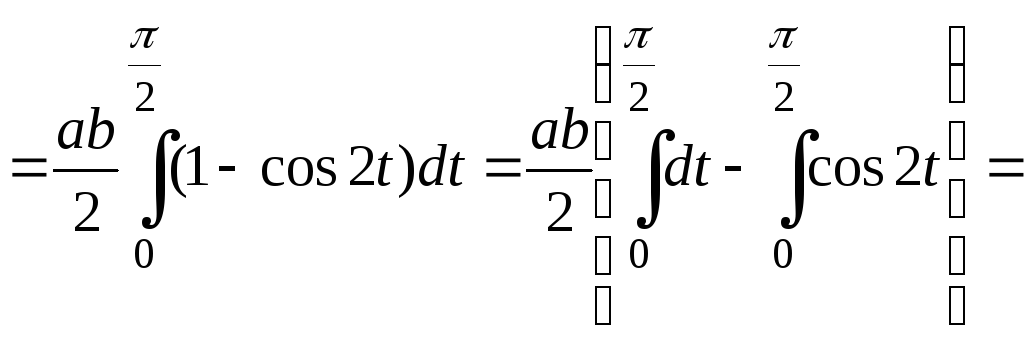
Окончательно, искомая площадь равна В частности, если, то получим известную формулу площади круга.

Замечание 3. Если криволинейная трапеция примыкает к оси , то аналогом формулы (3) является формула:

(3^a)

В рассмотренном выше примере изменению от0 до соответствует изменениеот0 до и поэтому.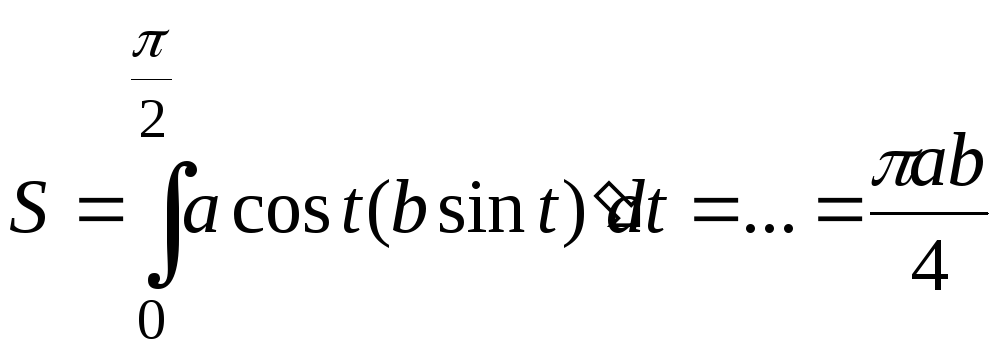

Замечание 4. Для фигур, ограниченными замкнутыми кривыми, можно применять комбинацию формул (3) и (3^а):

если только при естественном изменении параметра( т.е. от меньших значений к большим) точка пробегает границу фигуры в положительном направлении.

Пример 4. Найти площадь фигуры, ограниченной петлёй линии:

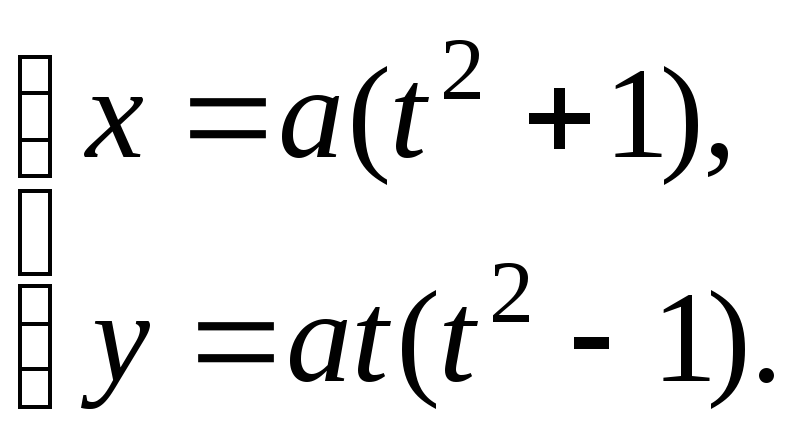
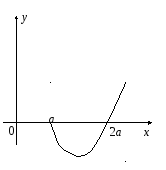
Решение. Абсцисса точки линии является чётной функцией параметра, а ордината – нечётной. Значит, если значению параметра соответствует точка, то значениюбудет соответствовать точка, т.е. кривая симметрична относительно оси. Рассмотрим уравнения линии дляЗначению параметрасоответствует точка. Далее, при увеличенииабсцисса точки растёт, т.е. точка движется вправо. Ордината же точкисначала убывает(для малых), а затем возрастает, т.е. точка сначала движется вниз, а затем вверх. Прилиния пересекает ось абсцисс в точке. Вспоминая о симметрии линии, получим: точкасоответствует не только значению, но и. Изменение параметра отдои даёт петлю линии, причём она пробегается против часовой стрелки.

Итак, для площади петли имеем: