Задача 2. Оценка «тесноты» связи между переменными

«Теснота» связи может быть оценена графически по расположению экспериментальных точек относительно теоретической линии регрессии.

Для количественной оценки «тесноты» и направлениялинейнойсвязи между переменными используетсякоэффициент корреляции:

;

.

Диапазон изменения коэффициента корреляции: .

Характерные значения коэффициента корреляции представлены на рис.2.10.

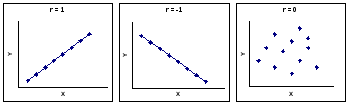
Рис.2.10. Граничные значения коэффициента корреляции

Считают:

- связь очень слабая;

- связь сильная;

- связь есть.

Для оценки «тесноты» связи при любой форме связи используется корреляционное отношение:

,

где

R²-коэффициент детерминации.

Диапазон изменения: .

Коэффициент детерминациипоказывает долю общей колеблемости (вариации, изменения, разброса) результатаY, объясняемой колеблемостью учитываемых факторов (X):

,

где

- межгрупповая дисперсия (факторная дисперсия), отражающая влияние только учтенных факторов (Х) на колеблемость результата (Y);

- общая дисперсия, отражающая влияние всех факторов (как учтенных, так и не учтенных) на колеблемость результата (Y).

Доказывается, что при выполнении определенных условий общая дисперсия может быть представлена суммой межгрупповой и остаточной дисперсии:

,

где

- остаточная дисперсия, оценивающая колеблемость результата Yпод влиянием всехнеучтенныхфакторов.

В силу определения R²принимает значения между 0 и 1.

Если R² = 0, то это означает, что регрессия ничего не дает.

Другой крайний случай R² = 1означает точную подгонку: все экспериментально полученные точки лежат на регрессионной прямой.

Чем ближе к 1 значение R², тем лучше качество подгонки,более точно аппроксимируетY.

Например, если R² = 0,80, то колеблемостьYна80%объясняетсяX.

Недостаток коэффициента детерминации – его значение не отображает направление связи между исследуемыми переменными.

Дисперсияхарактеризует рассеивание (степень «разброса») случайной величины вокруг еёматематического ожидания(среднего значения).

Если использовать обозначения:

- фактически полученные в эксперименте значения Yпри наблюдаемых значениях;

- расчетные (по оцененному аналитическому уравнению регрессии) значения Yпри наблюдаемых значениях;

- среднее значение Yдля данного массива экспериментально полученных данных,

то дисперсии могут быть вычислены по следующим выражениям.

Общая дисперсия

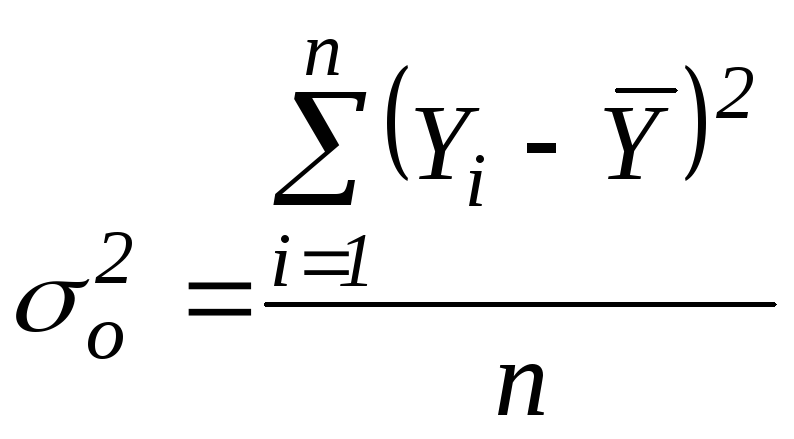. (2.1)

Межгрупповая дисперсия

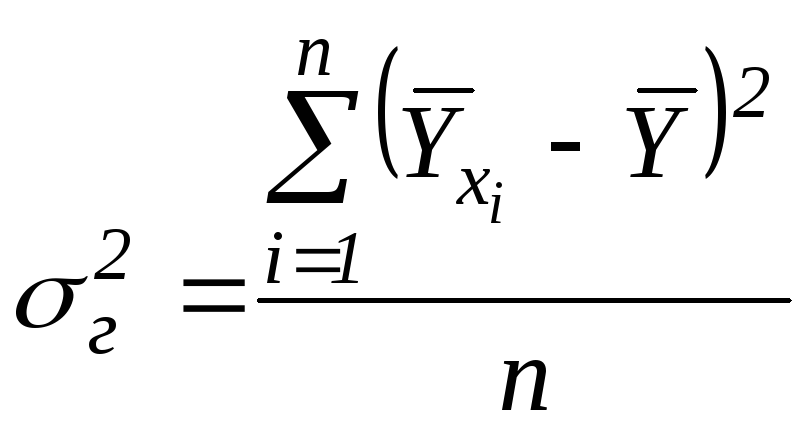. (2.2)

Остаточная дисперсия

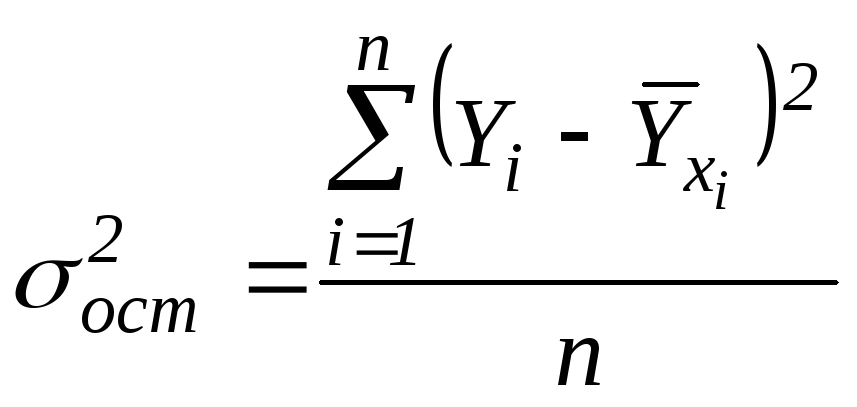. (2.3)

Внимание!"n" в формулах (2.1) – (2.3) должно быть обязательно одинаковым. Поэтому если при одном и том жев серии экспериментов получено несколько значенийY, расчетные значенияYнеобходимо вычислить при тех же, что и в эксперименте, т.е. взять столько точек, сколько в эксперименте.

Отобразим графически (рис.2.11).

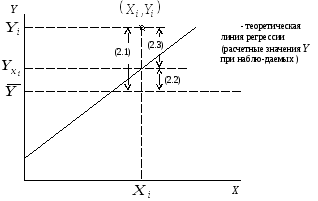
Рис.2.11. К вопросу определения общей, межгрупповой и остаточной дисперсии

Данные для расчета общей, межгрупповой и остаточной дисперсии для рассматриваемого примера представлены в табл.2.3.

Таблица 2.3 – Данные для расчета дисперсии

i
1	0,1444	0,16322	0,00058
2	0,0529	0,09181	0,00533
3	0,0169	0,00000	0,01690
4	0,0144	0,09181	0,03349
5	0,3844	0,16321	0,04665
Σ	0,6130	0,51005	0,10295

Тогда для рассматриваемого примера колеблемость Yобъясняется колеблемостьюXна 83,2%, т.к.

.