4.3. Уравнение плоскости, проходящей через три заданные точки

Требуется составить уравнение плоскости, проходящей через три точки

Пусть точка текущая

точка плоскости. Построим векторы

. Они компланарны,

т.е. их смешанное произведение

или

(2)

Пример 4. Составить уравнение плоскости, проходящей через начало координат и точки

Из уравнения (2) получим

4.4. Угол между двумя плоскостями

Пусть две плоскости заданы общими уравнениями

Очевидно, угол между двумя

плоскостями равен углу между их

нормальными векторами.

Из этого следует

(3)

Если плоскости перпендикулярны, то

Если плоскости параллельны, то их нормальные векторы коллинеарны и тогда условие параллельности принимает вид

Пример 5. Найти угол между плоскостями, заданными уравнениями и

По формуле (3) получаем

т.е. данные плоскости перпендикулярны.

4.5. Расстояние от точки до плоскости

Требуется найти расстояние от плоскостидо точки. М₀

Рассуждая аналогично, как и

для случая прямой на плоскости, d

получаем М

или

(4)

Пример 6. Составить уравнение плоскости, параллельной плоскости и отстоящей от неё на расстояние

Уравнение искомой плоскости в силу условия параллельности имеет вид Возьмём любую точку, принадлежащую плоскости, например, точку. Тогда, используя формулу (4), получим

или

т.е. и тогда получаем две плоскости, удовлетворяющие условию задачи,

Тема 5 : Прямая в пространстве

5.1. Уравнения прямой

Как известно, одним из способов задания прямой является пересечение двух непараллельных плоскостей, т.е. прямая l определяется системой уравнений

(5)

Кроме того, прямаяl будет определена,

если задать точку , принадлежащуюМ

прямой и вектор , которому эта

прямая параллельна. Такой вектор называетсяl М₀

направляющим вектором.

Пусть точка  текущая точка прямой, тогда из условия коллинеарности двух векторов иполучаем

(6)

Если обозначить равные отношения в формуле (6) через t, то получим

(7)

Уравнения прямой вида (5)(7) называются соответственно общими, каноническими и параметрическими. Между этими уравнениями существует определённая связь. Переход от уравнений (6) к уравнениям (7) уже рассмотрен. Пусть требуется перейти от уравнений (6) к уравнениям (5). Уравнения (6) эквивалентны системе

(8)

Система линейных уравнений (8) и определяет прямую как линию пересечения двух плоскостей. Для перехода от уравнений (5) к (6) необходимо найти из системы (5) координаты любой точки М₀, принад-лежащей прямой, а за направляющий вектор взять вектор .

Пример 7. Прямая задана общими уравнениями

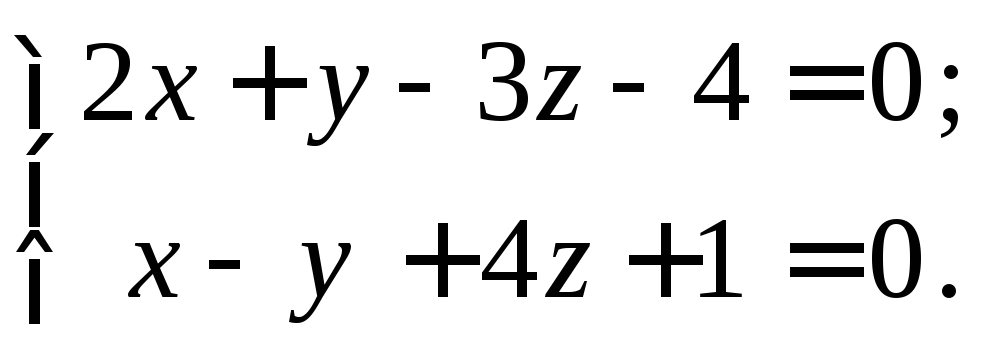
Требуется получить канонические и параметрические уравнения.

Полагая в системе , находим

Выпишем нормальные векторы и найдём их векторное произведение

Тогда канонические уравнения прямой имеютвид

и параметрические уравнения