2.8. Число е.

Рассмотрим последовательность 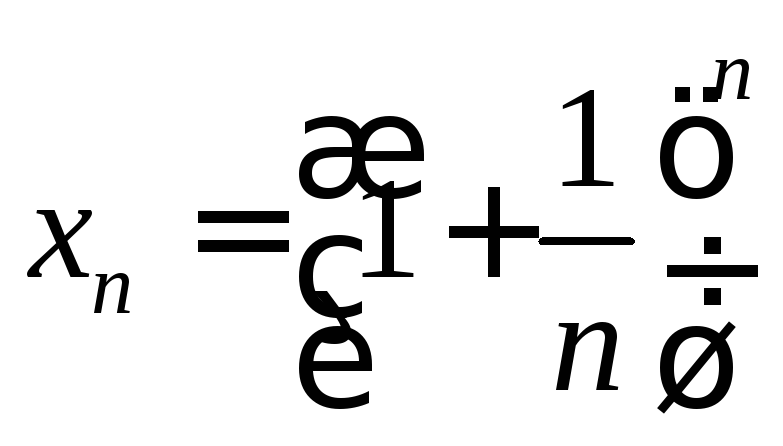. Покажем, что данная последовательность имеет предел.

Воспользуемся формулой бинома Ньютона, полагая .

Из этой формулы следует, что , так как все слагаемые суммы положительные. Покажем, что эта последовательность ограничена.

Таким образом, для получаем неравенство. Итак, последовательность возрастает и ограничена сверху, отсюда, по свойству5 последовательностей (п. 2.1), она имеет предел

,

где е  иррациональное число .

2.9. Второй стандартный предел

Теорема. . (2)

Если , то формула (2) уже доказана. Если, то его значение заключено между двумя положительными целыми числами

. (3)

Тогда будет выполняться

.

С учетом условия (3), получаем

. (4)

Если и тогда

Аналогично

Переходя в формуле (4) к пределу при , и учитывая теорему4 (п.2.5), получаем второй стандартный предел (2).

Замечание 2. Пусть , тогда, с учётом новой переменной, получим

Таким образом, .

Схематично график функцииизображен на рисунке.

у

е

1

1 0 х

Замечание 3. Если ввести новую переменную при, тогда

Пример 3. .

Пример 4. .

Пример 5.

.

2.10. Сравнение б.М.В.

Пусть и б.м.в. при .

Определение 1. Если , тоназывается б.м.в.более высокого порядка, чем прии пишут.

Пример 6. Пусть , тогда приполучаем

.

Определение 2. Если , тоиназываются б.м.в.одного порядка.

Пример 7. Пусть , тогда приполучаем

и  б.м.в. одного порядка.

Определение 3. Если , тоиназываютсяэкви-валентными б.м.в. и обозначаются при.

Из ранее рассмотренных пределов следует таблица эквивалентных б.м.в. при :

; ;;

; ;,

где последнее соотношение следует из бинома Ньютона, но оно справед-ливо и для

Легко показать, что предел отношения б.м.в. не изменится при замене их эквивалентными б.м.в., что используется при вычислении пределов.

Пример 8.

Пример 9.

Лекция № 17. Тема 3 : Непрерывность

3.1. Определение непрерывной функции

Пустьопределена в некоторой. Близкая к ней другая точка из этой окрестности может быть представлена в виде , гденазываетсяприращением аргумента. у

Разность

называется приращением функции в

точке х₀.

Определение 1. Функция назы-

вается непрерывной в точке х₀, если

она определена в точке х₀ и в некоторой х₀ х

её окрестности и

. (1)

Преобразуем равенство (1)

откуда следует

. (2)

Так как , то тогда формула (2) прини-мает вид

. (3)

Формула (3) является вторым эквивалентным определением непре-рывности функции в точкех₀, которое можно сформулировать следующим образом :

Определение 2. Функция называется непрерывной в точкех₀, если она определена в этой точке и некоторой её окрестности, имеет предел при и этот предел равен значению функции в этой точке.

Определение 3. Функция , непрерывная во всех точках некоторого промежутка называется непрерывной на этом промежутке.

Пример 1. Доказать, что функция непрерывна в своей области определения.

Имеем , где. Тогда получим

Замечание 1. Аналогично можно доказать, что все основные элемен-тарные функции непрерывны в области своего определения.