2.4. Теорема о пределе функции

Эта теорема является важной, так как используется при доказатель-стве многих теорем и утверждений.

Теорема. Если функция имеет предел при , то в некоторой окрестностиона представляется в виде суммы, гдеА  её предел, а  б.м.в. при . Верно и обратное.

Пусть , т.е.  б.м.в. или .

Обратно. Пусть . Тогда, т.е..

Замечание 4. Теорема остаётся справедливой и для случая . Тогда вместо фразы “в некоторой окрестности“ следует читать “при достаточно большихх“.

2.5. Основные теоремы о пределах

Предположим, что существуют пределы соответствующих функций. Тогда справедливы теоремы:

Теорема 1. Предел суммы конечного числа функций равен сумме пределов этих функций, т.е.

.

Теорема 2. Предел произведения конечного числа функций равен про-изведению пределов этих функций, т.е.

.

Следствия:

1. Если .

2. .

Теорема 3. Если , то.

Пусть иТогда по теореме о пределе функции имеем,, гдеи б.м.в. при .

Напишем тождество

Поскольку 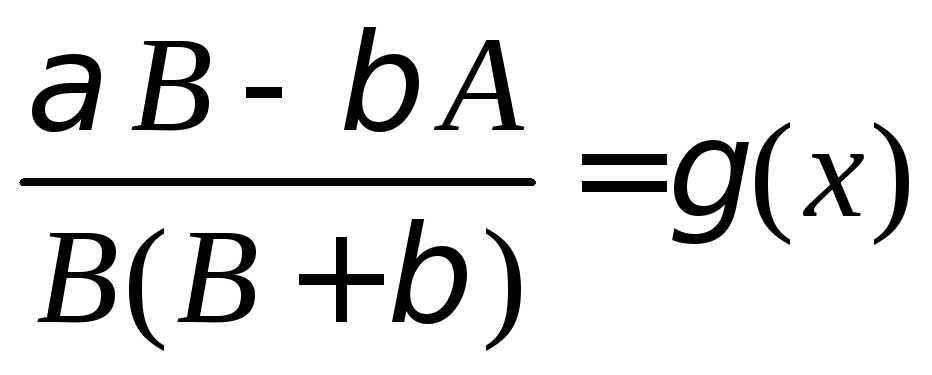является б.м.в. по свойствам б.м.в., то тогдаи по теореме о пределе функции получаем

, ч. т. д.

Утверждение следующей теоремы практически очевидно, а её дока-зательство следует из определения предела функции.

Теорема 4. Если в некоторой окрестности выполняетсяи, то.

Замечание 5. Доказательства теорем 1–2 аналогичны доказательству теоремы 3.

Покажем, как с помощью этих теорем вычисляются некоторые пределы.

Пример 3. Найти .

Так как , то имеем

2.6. Раскрытие неопределённостей

Рассмотрим пример: найти предел .

Здесь и.

Этот случай классифицируется как неопределённость вида . Известны также неопределённости следующих видов:и, если1 является пределом некоторой функции, то .

Чтобы раскрыть эти неопределённости, т.е. найти соответствующие пределы, необходимо выполнить соответствующие тождественные преобра-зования функции под знаком предела, которые зависят от вида неопре-делённости и самой функции. Рассмотрим это на конкретных примерах.

Пример 4. .

Пример 5. .

Пример 6.

Пример 7.

Лекция № 16

2.7. Первый стандартный предел

Теорема. . (1)

Выражение под знаком предела является неопределённостью вида. Раскроем данную неопределённость, C

исходя из геометрических соображений. A

Построим окружность с центром в R

точке и радиусомR. Выберем

угол х в первой координатной четверти х

и сравним площади трех фигур: AOB, О D B

сектор AOB и  СOВ.

Из рисунка видно, что площади

указанных фигур связаны соотношением:

.

Вычислим эти площади:

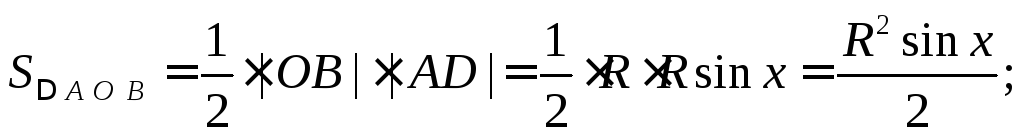
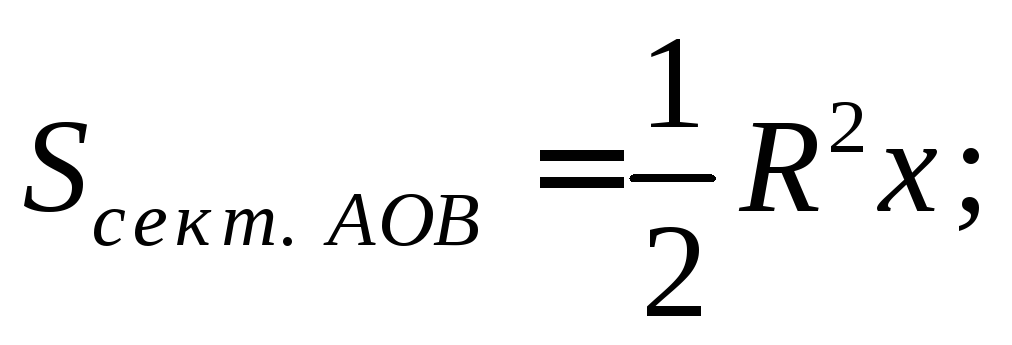
откуда имеем .

С учётом того, что , разделим обе части неравенства наи получим

или .

Так как , то на основании теоремы4 (п.2.5) имеем требуемое равенство (1).

Замечание 1. Правомерность предельного перехода под знаком косинуса будет показана в следующей лекции.

Пример 1.

Пример 2.