IV Полярные уравнения линии

Этот случай сводится к теореме 2, если использовать формулы, связывающие декартовы и полярныекоординаты точки:

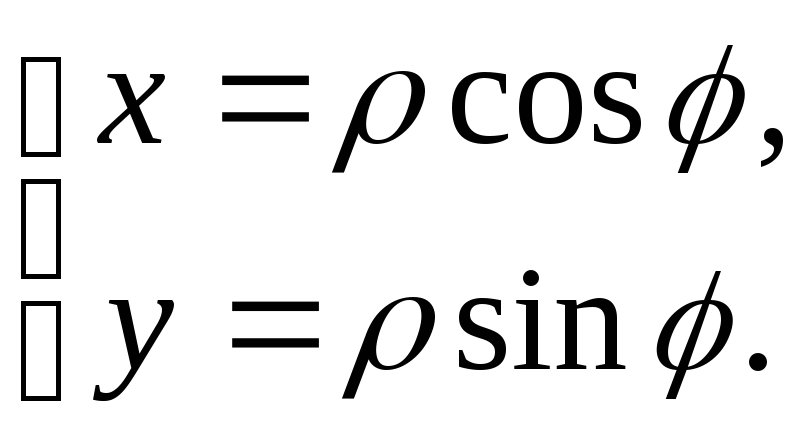
А. . Функция– непрерывно-диф-ференцируема. В этом случае имеем:

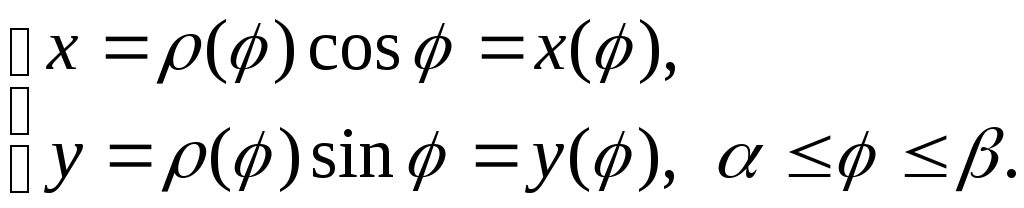
Вычисляем производные, возводим их в квадрат и складываем:

Итак, длина линии в этом случае выражается формулой

Пример 4. Вычислить длину части кардиоиды расположенной вне окружности.

Решение. Решим сначала неравенство

.

Итак, требуемая часть кардиоиды соответствует изменению отдо– это пределы интегрирования в формуле (3). Проведем теперь предварительные вычисления:

Т.к. , тои; на этом промежутке синус положителен.

Вычисляем длину:

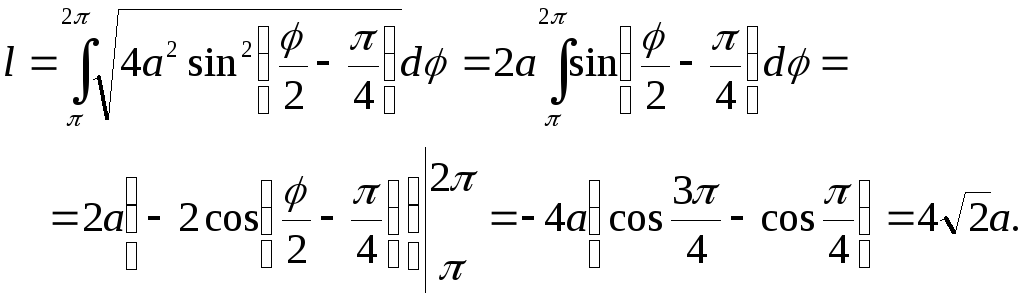
Предлагаем студентам самостоятельно рассмотреть еще 2 случая и получить нужные формулы:

В. –

С. –

Задачи (для самостоятельного решения)

1. Вычислить длину графика функций .

2. Вычислить длину петли линии .

3. Вычислить длину всей линии .

4. Найти радиус окружности, которая делит дугу астроиды на три равновеликие части.

5. Найти длину всей линии .

6. Найти длину дуги линии .

7. Найти длину дуги линии .

§4. Вычисление объёмов некоторых тел

I Понятие объёма тела. Объём цилиндра

Понятие объёма тела вводится аналогично понятию площади плоской фигуры: в данное тело вписывают многогранники и описывают вокруг тела. Их объёмы обозначими.

Определение 1. Пусть для данного тела существуют две после-довательности многогранниковитаких, что. Если, то телоназывают кубируемым, а число– его объёмом.

Как и в случае фигур, будем вписывать и описывать не многогранники, а другие тела (и наборы их), кубируемость которых уже доказана.

Дадим определение цилиндра и докажем его кубируемость.

Пусть в некоторой плоскости дана линияи пусть дана прямая, перпендикулярнаяи проходящая через точку. Поверхность, образованная движением прямой, когда в точкепробегает линию, называют цилиндрической поверхностью. При этом прямуюназывают образующей, а линию– направляющей поверхности.

Определение 2. Цилиндром называют тело, ограниченное цилинд-рической поверхностью с замкнутой направляющей и двумя плоскостями, перпендикулярными образующей. Части этих плоскостей, высекаемые цилиндрической поверхностью, называют основаниями цилиндра, а расстояние между ними его высотой.

Лемма. Цилиндр кубируем, если его основание квадрируемо; его объём равен произведению площади основания на высоту.

Доказательство. Пусть – высота, аоснование цилиндра ии– многоугольники такие, чтои. Построим прямые призмы, основаниями которых являютсяи. Эти призмы будут вписанными и описанными многогранниками. Из элементарной геометрии известно, что объём призмы равен произведению площади основания на высоту. А так как площади оснований (вписанных и описанных) – имеют равные пределы, то и объёмы многогранников будут иметь равные пределы. Это и означает кубируемость цилиндра.

II Вычисление объёма тела по его поперечным сечениям

Теорема 1. Пусть для данного тела известны площади сечений, перпендикулярных некоторому направлению, принятому за ось . Тогда объём тела выражается формулой

(1)

где – площадь сечения с абсциссойx, a и b – абсциссы крайних сечений тела (предполагается, что функция – непрерывна).

Идея доказательства. Отрезок разобьём на части точкамии, проведя плоскости, разложим тело на слои. Рассмотримk-й слой, расположенный между плоскостями и. На промежуткенепрерывная функциядостигает своего наименьшего и наибольшего значений:исоответственно. Если на этих, наименьшем и наибольшем сечениях построить цилиндры с высотой, то меньший цилиндр будет содержаться вk-м слое тела, а больший содержать в себе этот слой. Наборы этих цилиндров и дадут вписанные и описанные кубируемые тела. Объёмы этих тел, очевидно, равны:

и .

Но эти суммы – это интегральные суммы для функции , которые стремятся к единому пределу –Теорема доказана.

Пример 1. Найти объём эллипсоида

Решение. Сечение эллипсоида плоскостью – это эллипс

Его полуоси равны и, а площадь. Итак, функция, о которой идет речь в теореме 1, имеет вид

и объём эллипсоида дается интегралом

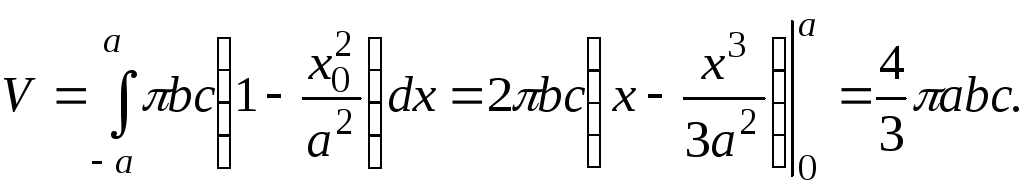
Пример 2. Найти объём «цилиндрического отрезка», т.е. части кругового цилиндра, отсекаемой плоскостью, которая проходит через диаметр основания.

Решение. Пусть основания цилиндра – это круг , секущая плоскость проходит через ось ординат и составляет уголс плоскостью основания – её уравнение. Через точкупроведем плоскость, перпендикулярную оси абсцисс. В сечении получим прямоугольник. Его основание – хорда круга, отстоящая от его центра на расстоянии. Её длина равна. Высота прямоугольника – отрезок образующей цилиндра между его основанием и секущей плоскостью. Его длина. Итак, площадь сечения с абсциссойимеет вид, а искомый объём получим проинтегрировавпо промежутку:

Этот результат можно записать в форме , где – высота «цилиндрического отрезка».