2.3 Метод наименьших квадратов

Один из видов точечной среднеквадратичной аппроксимации с помощью многочлена (2.2)

,

при этом 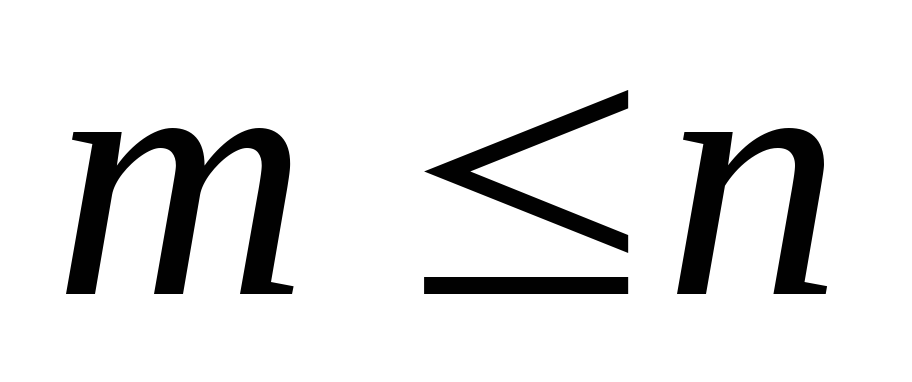(случайm=n соответствует интерполяции глобальной). Как правило, m=1,2,3, что, можно сказать, соответствует локальной интерполяции. Однако это не так. При интерполировании основным условием является прохождение графика интерполяционного многочлена через заданные таблично значения функции в узлах интерполяции. При среднеквадратичном приближении график аппроксимирующего многочлена проходит близко от таблично заданных значений функции.

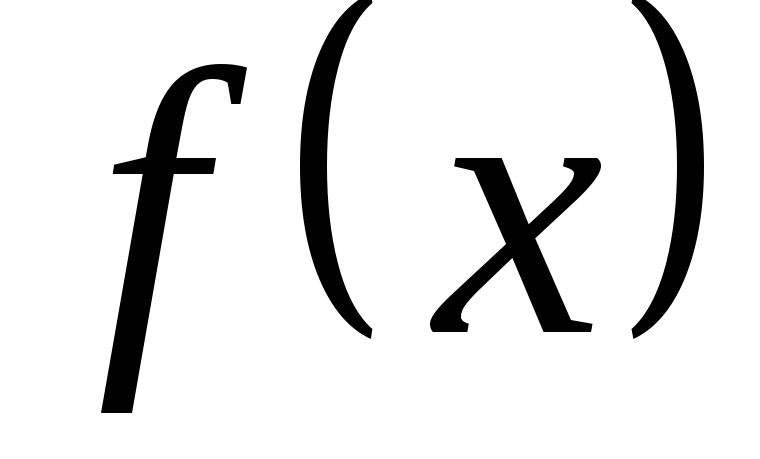Мерой отклонения аппроксимирующего многочлена от заданной функциина множестве точек,при среднеквадратичном приближении является величина

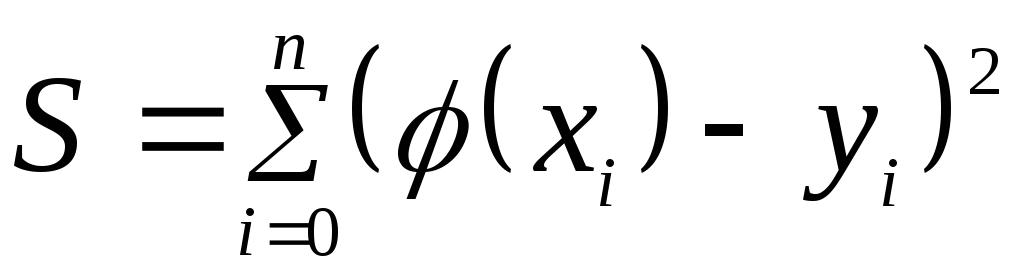
Для метода наименьших квадратов значение S должно быть минимальным. Это требование позволит нам определить коэффициенты аппроксимирующего многочлена.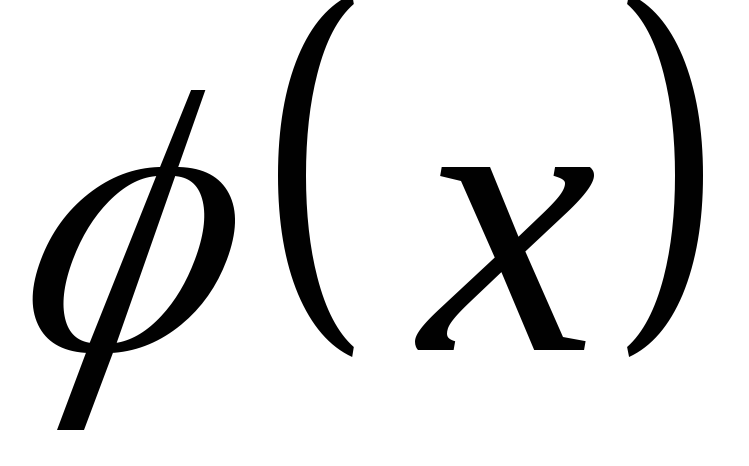

Т.к. в этой формуле параметры выступают в роли независимых переменных функцииS, то ее минимум найдем, приравнивая нулю частные производные по этим переменным

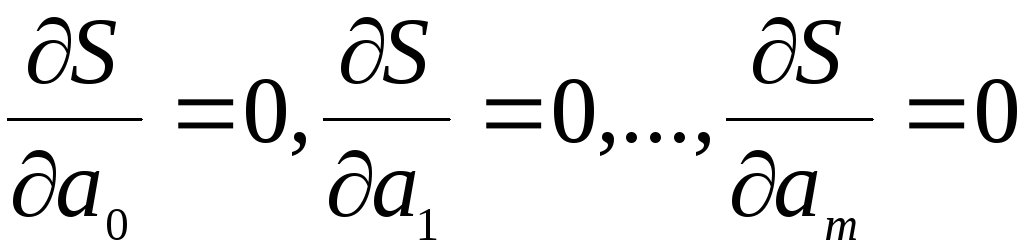
Полученные соотношения представляют систему из m+1 уравнений для определения

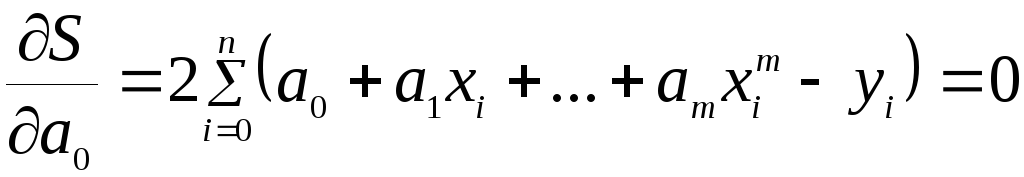
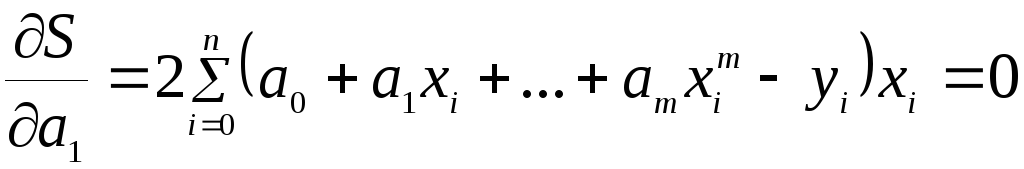
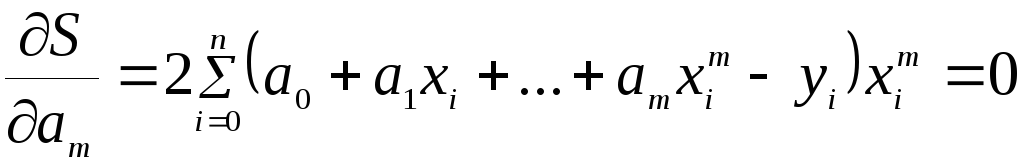
Преобразуя, получаем

…

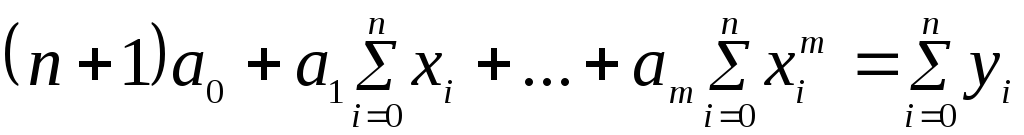
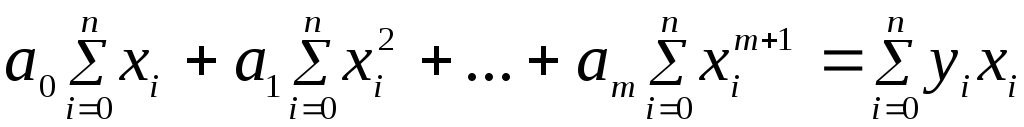
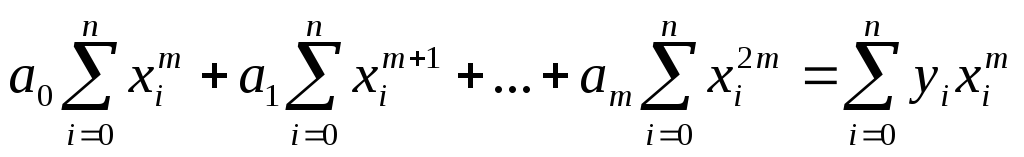
В компактной форме

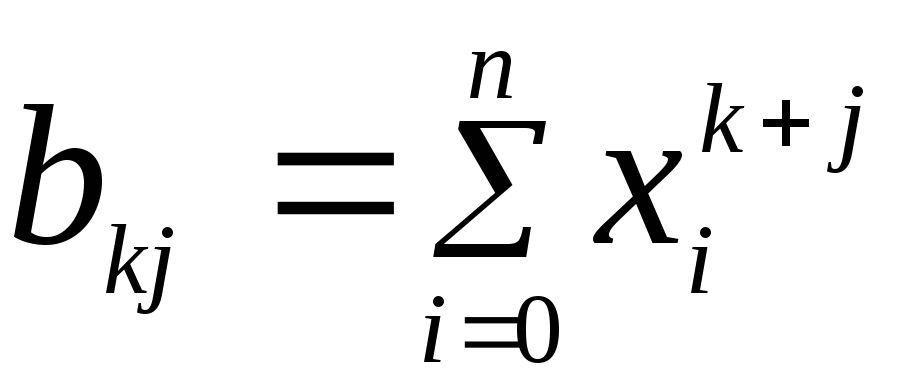
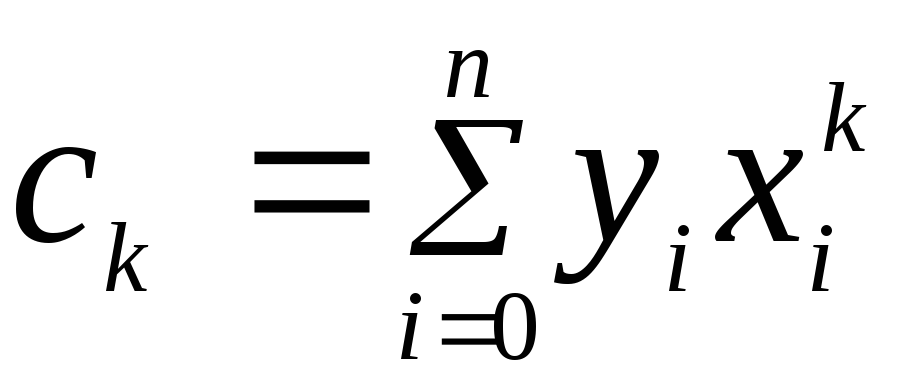
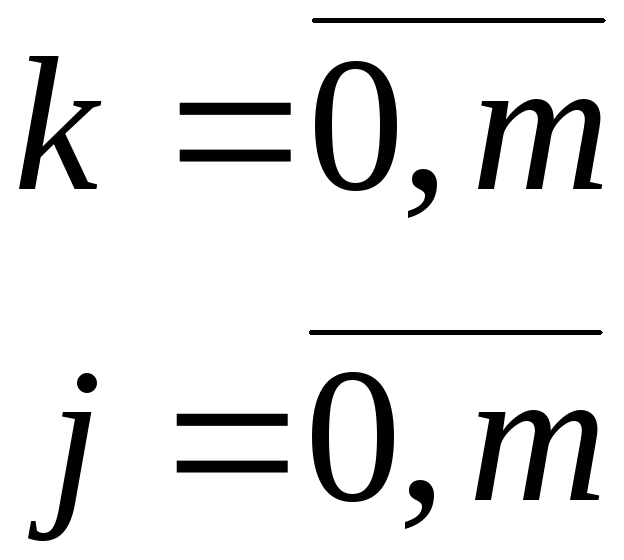
Система из m+1 линейного уравнения с m+1 неизвестным.