
Lektsii-DM
.pdf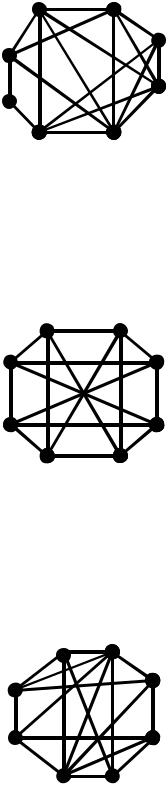
233
9.3 Завдання для самостійної роботи
1. Визначити, чи є граф G планарним, використовуючи критерій Понтрягина-Куратовського або Вагнера. Побудувати плоску укладку графа G , використовуючи алгоритм .
2. Визначити, чи є граф G планарним, використовуючи критерій Понтрягина-Куратовського або Вагнера. Побудувати плоску укладку графа G , використовуючи алгоритм .
3. Визначити, чи є граф G планарним, використовуючи критерій Понтрягина-Куратовського або Вагнера. Якщо вхідний граф був планарним додати мінімальне число ребер до непланарності. Для непланарного графу (вхідного чи перетвореного) визначити характеристики: рід, товщину, число схрещувань та перекрученість.
234
4. Нехай задано граф G множина вершин якого дорівнює N9 , а множина ребер складається за таким принципом: дві вершини із номерами i та j, i, j N9 є суміжними, якщо вони діляться без залишку чи на 7, чи на 8. Визначити, чи є граф G планарним, використовуючи критерій Понтрягина-Куратовського або Вагнера. Побудувати плоску укладку графа G . Якщо вхідний граф був планарним додати мінімальне число ребер до непланарності. Для непланарного графу (вхідного чи перетвореного) визначити характеристики: рід, товщину, число схрещувань та перекрученість.
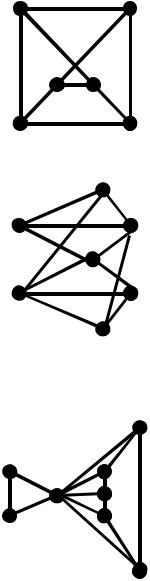
5.Для заданого графа G знайти хроматичне число та хроматичний індекс.
6.Для заданого графа G знайти хроматичне число та хроматичний індекс.
7.Послідовно розфарбувати граф G , знайти хроматичне число та хроматичний індекс.
8. Нехай задано граф G множина вершин якого дорівнює N8 , а множина ребер складається за таким принципом: дві вершини із номерами i та j, i, j N8
235
є суміжними, якщо вони діляться без залишку чи на 5, чи на 6. Для заданого графа G знайти хроматичне число та хроматичний індекс.
9. Нехай задано граф G множина вершин якого дорівнює N10 , а множина ребер складається за таким принципом: дві вершини із номерами i та j, i, j N10 є суміжними, якщо вони діляться без залишку чи на 7, чи на 9. Для заданого графа G знайти хроматичне число та хроматичний індекс.
10. Навести приклад графа, у якого число фарб для правильного розфарбування буде залежати від порядку обходу вершин.
9.4 Контрольні питання
1.Який граф називається плоским, планарним?
2.Що таке жорданова крива? Сформулювати теорему Жордано та наслідок із неї.
3.Дати визначення грані та границі грані плоского графа.
4.Сформулювати теорему Ейлера для плоского графа.
5.Операції підрозбиття та стягнення ребер графу. Гомеоморфні графи.
6.Сформулювати критерії планарності графів. Критерій ПонтрягинаКуратовського та Вагнера.
7.Алгоритм плоскої укладки графа. Дати визначення сегменту, контактної вершини, ланцюга, допустимої грані.
8.Дати визначення характеристикам непланарних графів: число схрещувань, товщина, рід графа, перекрученість.
9.Дати визначення вершинного та реберного розфарбування.
10.Яке розфарбування називається правильним? Привести опис алгоритму послідовного розфарбування.
11.Сформулювати визначення хроматичного числа, хроматичного
індексу.
12.Сформулювати теорему Кеніга та наслідків із неї. Дати визначення біхроматичного графу.

236
РОЗДІЛ 10 ОРІЄНТОВАНІ ГРАФИ (ОРГРАФИ)
10.1 Основні визначення теорії орієнтованих графів
Орієнтований граф G (V, A) – пара множин V і A , таких, що V – деяка кінцева непорожня множина, а A – деяка підмножина декартового квадрату множини V : V2 V V .
Вершини графа G – елементи множини V . Дуги графа G – елементи множини A. Дуга – упорядкована пара вершин a (u, v).
Початок дуги – вершина u, кінець дуги – вершина v.
Дуга виходить з свого початку і заходить у свій кінець.
Орграф G – орграф p -го порядку, якщо потужність множини вершин дорівнює | V | p .
10.2 Способи завдання орграфів
1.Матриця суміжності
A || aij |
||, i, j |
1,p, |
|
| V | p, | A | q . |
||
a |
|
1, |
(i, j) A |
|
||
ij |
|
(i, j) A |
|
|||
|
0, |
|
||||
2.Матриця інцидентності
B || bij ||, i 1, p, j 1, q, | A | q, | V | p. j (i, v) A .
|
1, |
i, v V, |
j (i, v) A |
|
1, |
i, v V |
j (v,i) A |
bij |
|||
|
0, |
else |
|
|
|
Наприклад.
Нехай маємо орграф G(V,A) порядку 4. Графічне зображення орграфу приведено нижче.

237
|
v1 |
a1 |
v2 |
|
|
|
|
a3 |
a2 |
a4 |
a5 |
v3 |
v4 |
Матриця інцидентності BG :
|
a1 |
a2 |
a3 |
a4 |
a5 |
v1 |
1 |
1 |
1 |
0 |
0 |
v2 |
1 |
0 |
0 |
1 |
1 |
v3 |
0 |
0 |
1 |
1 |
0 |
v4 |
0 |
1 |
0 |
0 |
1 |
Матриця суміжності AG : |
|
|
|
|
||
|
|
v1 |
v2 |
|
v3 |
v4 |
|
v1 |
0 |
1 |
1 |
1 |
|
|
v2 |
0 |
0 |
1 |
0 |
|
|
v3 |
0 |
0 |
0 |
0 |
|
|
v4 |
0 |
1 |
0 |
0 |
|
Основа – неорієнтований граф, що виходить внаслідок зняття орієнтації із дуг вхідного орграфа.
Зворотній орграф G 1 (V,A 1 ) – орграф, у якого множина вершин
збігається із множиною вершин орграфу G , і дуга (u, v) A 1 (v,u) A .

238
1 |
2 |
1 |
2 |
3 |
4 |
3 |
4 |
Зворотній орграф G 1 |
|
Основа G |
|
10.3 Степінь вершини орграфа
Напівстепінь заходу вершини v графа G – кількість дуг, що заходять у
вершину v : |
deg (v) |
|
|
|
X |
|
; |
X {x | x (u, v) A}. |
||
|
|
|||||||||
Напівстепінь виходу вершини v графа G – число дуг, що виходять із |
||||||||||
вершини v : |
deg (v) |
|
Y |
|
; |
Y {y | y (v,u) A}. |
||||
|
|
|||||||||
Степінь вершини v графа G – сумма півстепеней заходу та виходу у |
||||||||||
вершині v : |
deg(v) deg (v) deg (v) . |
|||||||||
Лема про рукостискання для орграфів
Сума напівстепеней заходу всіх вершин орграфа G дорівнює сумі напівстепеней виходу та дорівнює кількості дуг орграфа:
p |
p |
|
|
|
deg (vi ) deg - (vi ) |
q , |
q | A |, |
p | V | . |
|
i 1 |
i 1 |
|
|
|
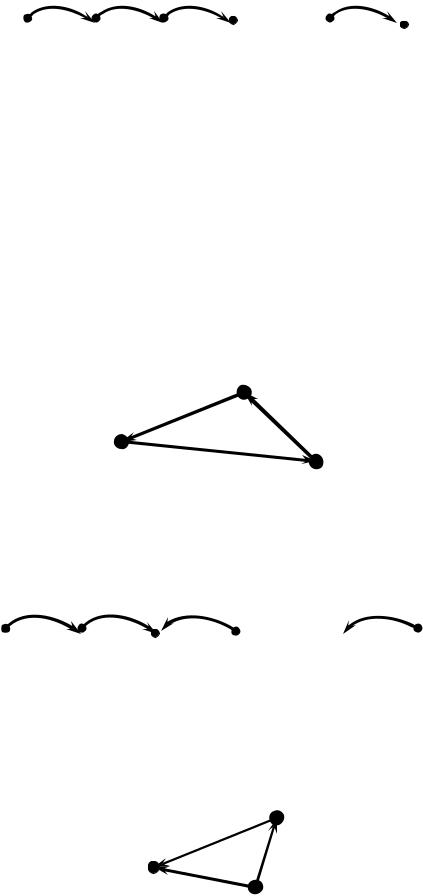
10.4 Маршрути в орграфах Орієнтований маршрут (ормаршрут) – кінцева послідовність, що
чергується з вершин дуг графа таких, що кожна дуга виходить з попередньої вершини і заходить у наступну вершину ai (vi , vi 1 ) :
239
a1 |
a2 |
a3 |
|
ak |
|
|
|
… |
|
v1 |
v2 |
v3 |
vk |
vk 1 |
Орієнтований ланцюг (орланцюг) – орієнтований маршрут без дуг, що повторюються.
Шлях – ланцюг без повторюваних вершин.
Орієнтований цикл (орцикл)– замкнутий орієнтований ланцюг. Контур – замкнутий шлях або или замкнутий шлях без повторення дуг та
вершин (окрім, можливо, крайніх).
Довжина орієнтованого маршруту – число дуг, що складають маршрут з урахуванням повторення.
Приклад контура.
Напівмаршрут (маршрут основи) – послідовність вершин і дуг орграфа,
така, що ai (vi 1 , vi ) або ai (vi , vi 1 ) .
|
a1 |
a2 |
a3 |
|
ak |
|
|
|
|
… |
|
v0 |
v1 |
v2 |
v3 |
vk 1 |
vk |
Аналогічно вводяться поняття напівланцюг, напівшлях, напівконтур.
Приклад напівконтура.

240
10.5 Типи зв'язності у орієнтованому графі
Вершина v орграфа G досяжна з вершини u, якщо існує (u,v)-ормаршрут в G, відповідно вершина u – контрдосяжна для вершини v.
Будь-яка вершина вважається досяжною сама для себе.
Вершини v и u орграфа G – взаємнодосяжні, якщо вершина v досяжна для вершини u, і вершина u досяжна для вершини v.
Орграф G – сильнозв’язний (сильний), якщо будь-які дві вершини в ньому взаємнодосяжні.
Орграф G – односторонньо зв’язний (односторонній), якщо для кожної пари його вершин, принаймні, одна досяжна з іншої.
Орграф G – слабозв'язний (слабкий), якщо будь-які дві його вершини з'єднані напівмаршрутом (напівшляхом).
Орграф G – незв’язний, якщо не зв’язна його основа.
Сильна компонента – максимальний щодо включення вершин сильний підграф вхідного орграфа.
Одностороння компонента – максимальний щодо включення вершин односторонній підграф вхідного орграфа.
Слабка компонента – максимальний щодо включення вершин слабкий підграф вхідного орграфа.
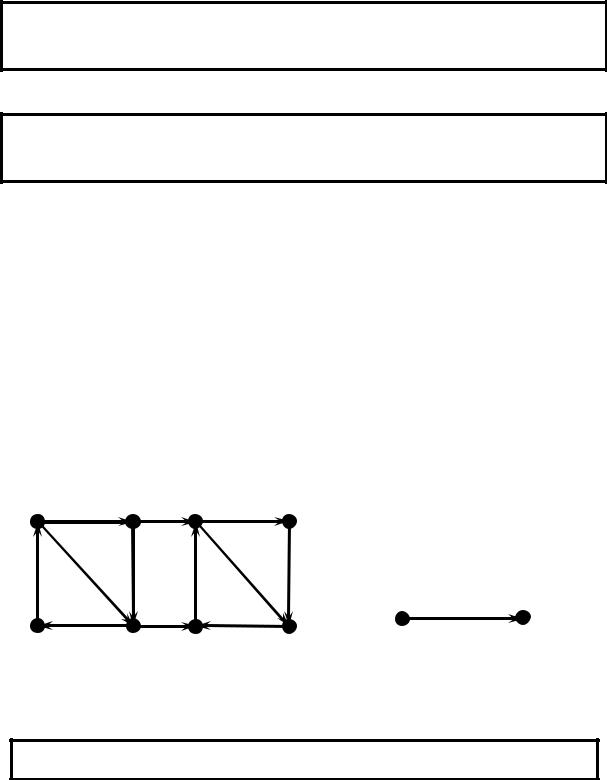
Сильний орграф |
Односторонній орграф |
Слабкий орграф |
10.6 Критерії сильної, односторонньої та слабкої зв’язності у орграфах
Орграф є сильним тоді і тільки тоді, коли в ньому є остовний циклічний ормаршрут.
241
Остовний маршрут – маршрут, що містить усі вершини вхідного графа.
Орграф є одностороннім тоді і тільки тоді, коли в ньому є остовний маршрут.
Орграф є слабким тоді і тільки тоді, коли в ньому є остовний напівмаршрут.
10.7 Конденсація орграфа
Конденсація орграфа G – орграф G , вершини S1 ,S2 ,...,Sm якого відповідають сильним компонентам орграфа G і дуга (Si ,Sj ) належить орграфу
G тоді і тільки тоді, коли в G існує дуга, початок якої, знаходиться в сильній
компоненті Si , кінець – |
в Sj . |
|
|
|
|
|
Наприклад. |
|
|
|
|
|
|
1 |
8 |
7 |
6 |
Сильні компоненти G |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
S1 {1,2,3,8} |
|
|
|
|
|
|
S2 {4,5,6,7} |
2 |
3 |
4 |
5 |
|
|
S2 |
S1 |
||||||
|
Орграф G |
|
Орграф G |
|
– конденсація G |
|
|
|
|
|
|
||
Конденсація G будь-якого орграфа G не має контурів
Алгоритм побудови конденсації
1. Побудуємо матрицю досяжності орграфа G .

 5
5 
 6
6