
Lektsii-DM
.pdf
123
Нехай задано неорієнтований граф G (V,E). V {v1 , v2 , v3 , v4 } – множина вершин графа. E {e1 ,e2 ,e3 ,e4 ,e5 } – множина ребер графа.
| V | 4 – порядок графа. Граф G – 4-граф або (4,5) -граф.
|
|
|
|
|
|
|
|
v2 |
|
|
|||||||||
|
|
e1 |
|
|
|
|
|
|
e2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
e3 |
v3 |
|
|||||||
v1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e4 |
|
|
|
|
|
|
|
e5 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
v4 |
|
|
|||||
3) Матричні способи опису неорграфів |
|
|
|||||||||||||||||
Матриця суміжності – квадратна матриця: |
|
|
|||||||||||||||||
|
|
AG |
|
aij |
|
,i, j |
|
|
, де |
|
|
||||||||
|
|
|
|
1,p |
|
|
|||||||||||||
|
a |
|
1, |
|
|
e i, j E |
. |
|
|||||||||||
|
ij |
|
|
|
e i, j E |
|
|||||||||||||
|
|
0, |
|
|
|
|
|||||||||||||
Матриця інцидентності – прямокутна матриця: |
|
||||||||||||||||||
|
BG |
|
bij |
|
,i |
|
j |
|
, де |
|
|
||||||||
|
|
|
1,p; |
1,q |
|
|
|||||||||||||
1, |
|
i |
V , j E , k V : j {i, k } |
. |
|||||||||||||||
b ij |
|
i |
V , j E, k V : j {i, k } |
||||||||||||||||
0, |
|
|
|||||||||||||||||
Наприклад.
Задано граф G (V,E), де V {a, b, c, d}, E {ab, bc, ac, ad, cd}.
Матриця суміжності AG : |
|
|
|
|
|
|
|
а |
b |
c |
d |
|
|
|
|
|
|
|
а |
0 |
1 |
1 |
1 |
|
|
|
|
|
|
|
b |
1 |
0 |
1 |
0 |
|
|
|
|
|
|
|
c |
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
d |
1 |
0 |
1 |
0 |
|
|
|
|
|
|

124
Матриця інцидентності BG : |
|
|
|
|
|
|
|||
|
|
ab |
|
bc |
ас |
|
ad |
сd |
|
|
|
|
|
|
|
|
|
|
|
|
а |
1 |
|
0 |
1 |
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
b |
1 |
|
1 |
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
c |
0 |
|
1 |
1 |
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
d |
0 |
|
0 |
0 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
5.3 Степінь вершини у неорграфах |
|
|
|
||||||
Степенем або валентністю вершини |
v |
неорієнтованого графа G |
|||||||
називається число ребер, що є інцидентними даній вершині. Степінь вершини позначається, як
deg(v), deg(v) | {e {u, v}: e E}| .
Максимальний степінь усіх вершин графу G – (G) :
(G) MAX deg(v) .
v V
Мінімальний степінь усіх вершин графу G – (G) :
(G) MIN deg(v).
v V
Оточенням вершини v називається множина усіх вершин графа G , суміжних з нею і позначається N(v) .
Наприклад.
v2
v3
v1
v4
deg(v1 ) 3,deg(v2 ) 2,deg(v3 ) 3,deg(v4 ) 2 ; (G) 3, (G) 2 ;
N(v1 ) {v2 , v3 , v4 }, N(v2 ) {v1 , v3 } ;
N(v3 ) {v1 , v2 , v4 }, N(v4 ) {v1 , v3 }.
125
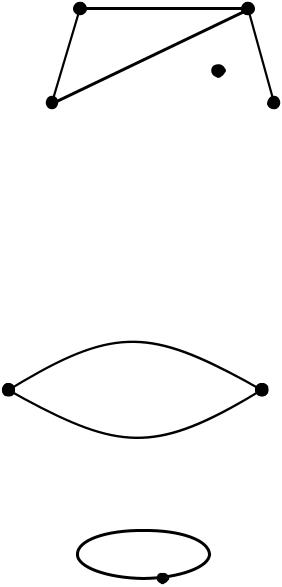
Вершина v графа G називається ізольованою, якщо її степінь дорівнює нулю, deg(v) 0 .
Вершина v графа G називається висячою або кінцевою, якщо степінь цієї
вершини дорівнює одиниці, deg(v) 1. |
|
Вершина v (p,q)-графа G називається |
домінуючою, якщо її степінь |
дорівнює p 1, deg(v) p 1 . |
|
Наприклад. |
|
V2 |
V3 |
V5
V1 |
V4 |
Унаведеному графі нема домінуючої вершини, ізольована вершина – v5 , висяча вершина – v4 .
Узагальному випадку у множині E допускається більш ніж одне ребро із однаковими кінцевими вершинами.
Такі ребра називаються паралельними або кратними.
v1 v2
v2
Ребро, що з’єднує вершину v саму з собою, називають петлею.
v
Граф, що не містить петель, але містить кратні ребра, називається
мультиграфом.

126
v1 |
v2 |
v3
Граф, що містить й петлі, й кратні ребра називається псевдографом.
V2
V1 |
V3 |
Граф, що не містить петель й кратних ребер називається звичайним. Далі, якщо не буде особливо обумовлено, розглядаються звичайні
скінченні графи.
Лема про рукостискання
Сума степеней усіх вершин неорієнтованого звичайного графу G (V,E),| V | p, | E | q є парною та дорівнює
p
подвоєному числу ребер: deg v 2q 2 E .
i 1
Доведення.
Кожне ребро графа інцидентно двом вершинам, тому воно додає до суми степеней вершин графа число два. Оскільки кількість ребер q , отже, сума всіх степеней вершин графа дорівнює 2q та є парним числом.

127
Слідство леми про рукостискання
У будь-якому неорієнтованому звичайному графі число вершин непарним степенем парним
|
|
Доведення. |
|
|
Без |
втрати спільності |
вважатимемо, що |
степінь перших r |
вершин |
v1 ,..., vr |
– є парним числом, а степінь (p - r) вершин, що лишилися – непарне |
|||
число. Тоді, суму S усіх степеней вершин графу можна представити, як суму |
||||
двох доданків: |
|
|
|
|
|
p |
r |
p |
|
|
S deg vi S1 S2 deg vi deg vi . |
|
||
|
i 1 |
i 1 |
i r 1 |
|
За лемою про рукостискання маємо, що S – парне число: |
|
|||
|
|
p |
|
|
|
|
S deg vi 2q . |
|
|
|
|
i 1 |
|
|
S1 |
– сума степеней перших r вершин графу є парним числом, |
як сума |
||
парних чисел, тоді S2 – сума степеней n r вершин графу, що осталися також парна, як різниця парних чисел: S2 S S1 2q S1 . Кожен доданок в сумі S2 є непарним числом, отже кількість доданків парна.
5.4 Спеціальні графи
Граф, що не містить жодного ребра, називається порожнім графом й позначається Op , де p – кількість вершин графа.
Граф, що не містить жодного ребра, жодної вершини, називається 0- графом (нуль-граф).
Тривіальний граф – (1,0)-граф.
Граф, G називається повним, якщо усі його вершини суміжні між собою або кожна його вершина є домінуючою.
Повний граф позначається Kp , де p – кількість його вершин.
Приклади зображень повних графів.

128
K3 |
K4 |
K5 |
K1 K2
Однорідний або регулярний граф – це граф, у якого ступені всіх вершин
рівні.
Усі повні графи є регулярними. Приклади регулярних графів. Граф Петерсона
deg=2 |
deg=3 |
Дводольні або біграфи
Граф G (V,E) називається дводольним або біграфом, якщо множину
його вершин |
V можна |
розбити |
на 2 непересічні підмножини V |
та V , |
|
|
|
1 |
2 |
V1 ,V2 V, V1 |
V2 , |
V1 V2 |
V такі, що будь-яке ребро графа має одну |
|
кінцеву вершину у V1 , а іншу у V2 . |
|
|
||
129
Якщо у звичайному дводольному графі G (V,E) із розбиттям (V1 ,V2 ) :vi V1 , vj V2 e {vi , vj } E , то такий дводольний граф називається
повним дводольним графом.
У повному дводольному графі довільна вершина із однієї долі суміжна довільній вершині із другої долі, й навпаки.
Позначається повний дводольний граф, як:
Kp1 ,p2 , де V1 p1, V2 p2.
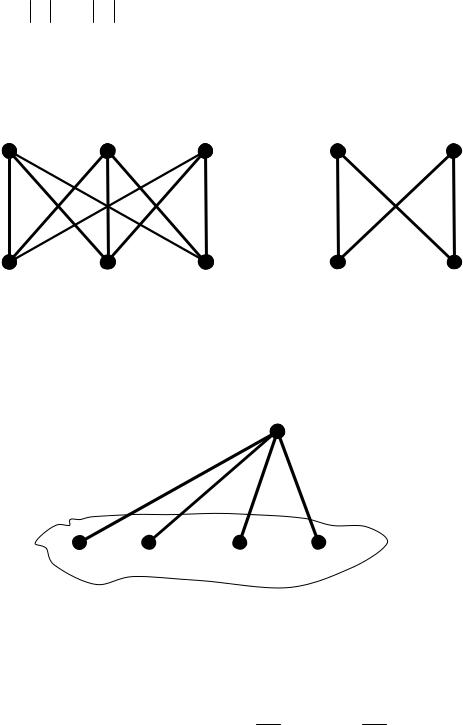
На рисунку представлено повні дводольні графи K3,3 (із відомої задачі про три будинки та три колодязі) та K2,2 .
Повний дводольний граф K1,n називається зіркою.
На рисунку зображено зірку K1,4 .
k -дольні графи
Граф G (V,E) називають k -дольним, якщо множину його вершин V
можна розбити на підмножини Vi ,i 1,k , i, j 1,k, i j: Vi Vj ,

130
k
i 1Vi V таким чином, що будь-яке ребро графа має одну кінцеву вершину в
Vi , а іншу – в Vj .
На рисунку зображено тридольний граф.
Зауваження: вершини однієї підмножини у k -дольному графі несуміжні між собою.
5.5 Підграфи
Неорієнтований граф G (V,E) називають позначеним або перенумерованим, якщо кожній вершині графа поставлена у відповідність унікальна мітка (число, символ). Інакше граф називається абстрактним.
Позначений граф Абстрактний граф
V1
V4 |
V2 |
V3
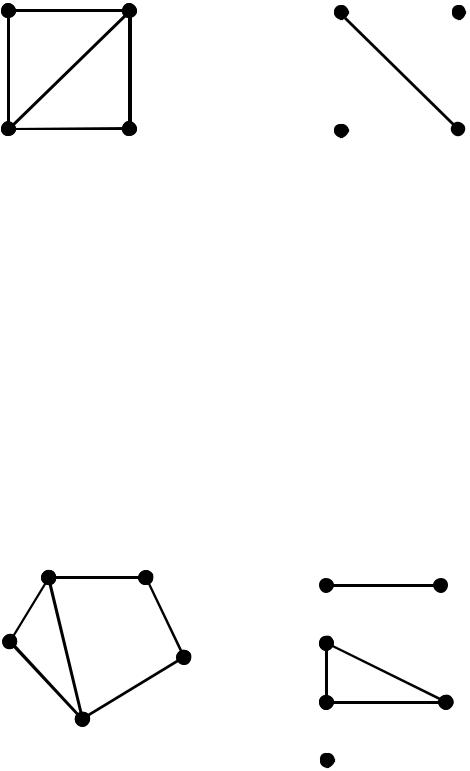
Граф G (V,E) називається доповненням графа G (V,E), якщо
множина вершин графів збігається, тобто V V , а множина ребер дорівнює
E V(2) \ E .
131
V1 |
V2 |
V1 |
V2 |
V3 |
V4 |
V3 |
V4 |
|||
Граф G |
|
Доповнення |
|
|
||
|
G |
|
||||
Множина вершин графа G і його доповнення збігається та будь-які дві |
||||||
вершини, що суміжні в G , несуміжні в його доповненні |
|
. |
|
|
||
G |
|
|||||
Доповнення графа G – |
це доповнення G до повного графа, на тій же |
|||||
множині вершин. |
|
|
|
|
|
|
Підграфом графа G (V,E) називається такий граф G1 (V1 , E1 ), у якого множина вершин є підмножиною множини вершин графу G , а множина ребер є
також підмножиною множини ребер графу G : V1 V, E1 E . |
|
|||
|
Граф G |
Підграфи G1 ,G2 ,G3 графу G |
||
V1 |
V2 |
|
G1 |
|
|
|
V1 |
|
V2 |
V5 |
|
V1 |
G2 |
|
V3 |
|
|
||
|
|
|
|
|
|
V4 |
V5 |
G3 |
V4 |
|
|
|
||
|
|
V1 |
|
|
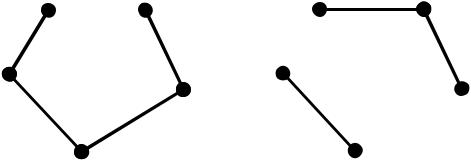
Остовним |
підграфом графа |
G (V,E) називається |
такий підграф |
|
G1 (V1 , E1 ), у якого множина вершин дорівнює множині вершин графу G , а множина ребер є підмножина множини ребер графу G : V1 V, E1 E .
132
Породженим підграфом графа G (породженим множиною вершин V1 ) називається підграф G1 (V1 , E1 ), такий, що V1 V, E1 E й ті вершини, що суміжні у графі G , будуть також суміжні у породженому підграфі.
Наприклад.
1)Для графу G , зображеного на попередньому рисунку, граф G1 є підграф, породжений множиною вершин {v1 , v2 }, G2 є підграф, що породжений множиною вершин {v1 , v4 , v5 }, а граф G3 є підграф, породжений множиною вершин {v1 }.
2)Графи G4 ,G5 для того ж графу G являються остовними підграфами.
|
G4 |
|
G5 |
V1 |
V2 |
V1 |
V2 |
V5 |
V3 |
V5 |
V3 |
|
|
V4 |
V4 |
5.6 Ізоморфізм графів
Два графи G і H називають ізоморфними, якщо існує взаємно однозначна відповідність (бієкція) між множинами їх вершин така, що зберігається відношення суміжності, позначення G H .
Наприклад.
|
|
|
|
|
|
|
1) Графи G та H ізоморфні між собою, бієкція V V , що доводить |
||||||
цей факт, наведена у таблиці. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u V |
v1 |
v2 |
v3 |
v4 |
|
|
|
|
|
|
|
|
|
(u) V |
v4 |
v3 |
v2 |
v1 |
|
