Lektsii-DM

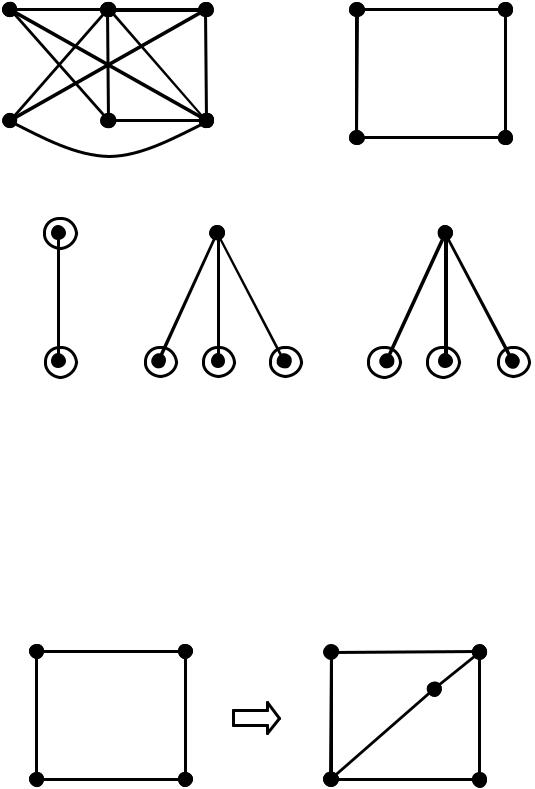
223

1) Визначимо множину сегментів відносно поточної плоскої укладки.

224

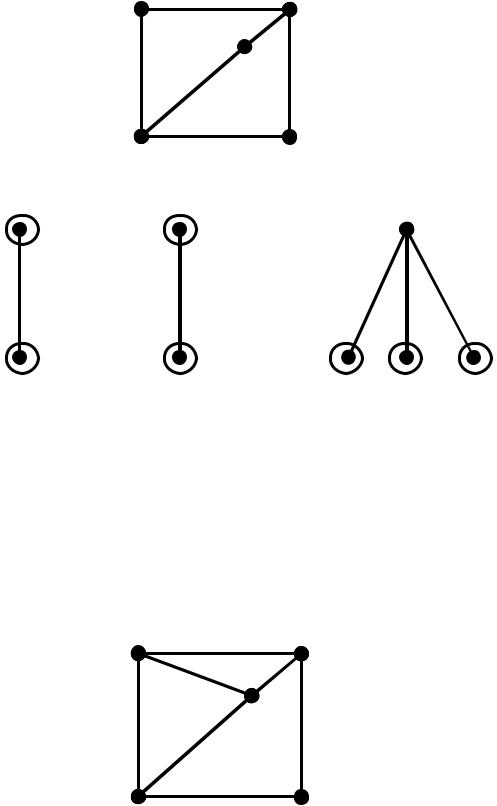
2) Для нової поточної плоскої укладки визначаємо нові множини граней і сегментів.

Для кожного сегмента визначимо множини допустимих граней:

(S1) { 1, 2, 3} , (S2) { 2}, (S3) { 1, 3}.

Обираємо сегмент S2 і укладаємо його в єдину для нього допустиму грань2 . Отримуємо поточну часткову плоску укладку графа G .

225

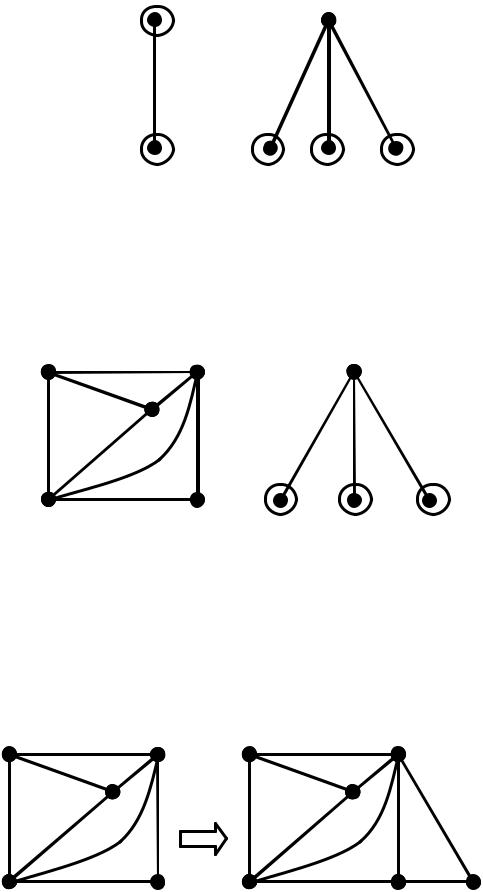
Множини допустимих граней для сегментів: (S1) (S3) { 1, 3}. Обираємо сегмент S1 та укладаємо до допустимої для нього грані 3 .

4) Отримуємо нову часткову укладку. Визначаємо для неї множину граней та сегментів.

226

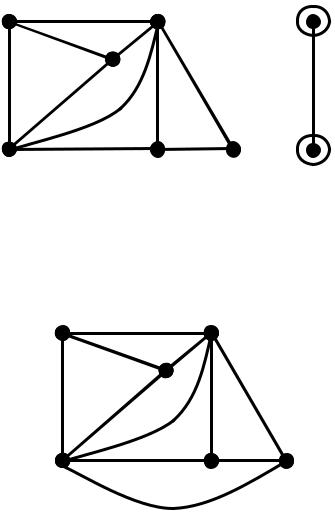
5) Для нової поточної часткової укладки знаходимо множину граней та сегментів.

Для сегмента S3 множина допустимих граней складає: (S3) { 1}. Укладаємо сегмент S3 до допустимої грані 1.

Отримуємо нову поточну плоску укладку. Множина сегментів порожня, отже, алгоритм закінчив роботу. Вхідний граф – планарний і побудована його плоска укладка.

Г1

9.1.6 Характеристики непланарних графів

Граф G укладається у простір L , якщо існує таке відображення вершин та ребер графа G відповідно у точки та жорданові криві цього простору, що різним вершинам відповідають різні точки простору, а криві, що відповідають різним ребрам, перетинаються тільки у інцидентних цім ребрам вершинах.

Наведені нижче характеристики графів представляють ту чи іншу міру непланарності.

227

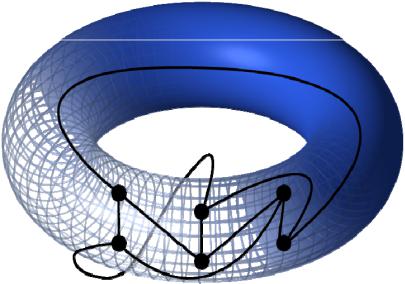
Кількість схрещувань графа G – це мінімальна кількість пересічень двох ребер при зображенні графа G на площині, позначають Cr(G).

Поняття пересічення відноситься до пересічення рівно двох ребер. Кількість схрещувань дорівнює 0 тоді і тільки тоді, коли граф є

планарним.

Перекрученість G – це мінімальна кількість ребер, видалення яких призводить до планарного графа, Sk(G) .

Товщина G – максимальна кількість його планарних підграфів, об’єднання яких дає граф G , позначають t(G).

Вочевидь, що товщина планарного графа дорівнює одиниці.

Рід графа G це мінімальна кількість ручок, які необхідно додати до сфери, щоб можна було укласти граф без пересічень та самопересічень ребер.

Графи, які не можна укласти на площині, але можна укласти на торі (сфері із однією ручкою), називають тороїдальними.

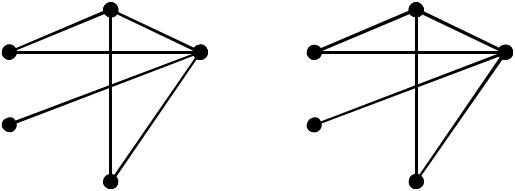
Граф K3,3 укладається на торі без пересічень и самопересічень ребер, рід такого графа дорівнює 1.

Тороідальними являються наступні графи: K5 , K7 , K3,3 , K4, 4 .

Приклад укладки графа K 3,3 на торі.

228

9.2 Розфарбування графів

9.2.1 Вершинне розфарбування

Нехай є неорієнтований граф G і нехай k – деяке натуральне число.

Вершинне k -розфарбуванням або k -розфарбуванням графа G

називається довільна функція f , що відображає множину вершин графа G у деяку k -елементну множину:

f: V {a1 ,a2 ,...,ak } A .

Уякості елементів множини A найчастіше використається відрізок

натурального ряду Nk {1, 2, ..., k} або {a, b, ..., n} або фарби типу {синій, червоний, ..., чорний}.

Розфарбування називається правильним, якщо для будь-яких суміжних вершин u і v графа G : f (u) f(v) або кінцеві вершини будь-якого ребра пофарбовані в різні кольори.

Граф, для якого існує правильне k-розфарбування, називається k-

розфарбованим.

Хроматичне число графа G – це мінімальне число фарб, при якому граф має правильне розфарбування.

Якщо хроматичне число дорівнює k, то граф називається k-хроматичним:

229

(G) = k.

Правильне k-розфарбування графа G можна представити як розбиття множини вершин графа G на не більш ніж k непустих множин, які називаються

однокольоровими класами: V V1 V2 ... Vk .

Кожний кольоровий клас є незалежною множиною вершин. Для повного графа Kp хроматичне число дорівнює: (Kp ) p .

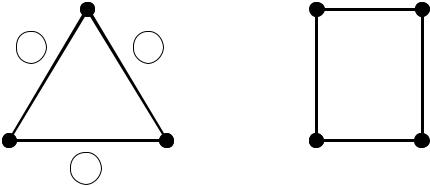
Для простого циклу із парним числом вершин: (C2p ) .

Для простого циклу із непарним числом вершин: (C2n 1 ) 3. Для порожнього графу: (On ) 1 .

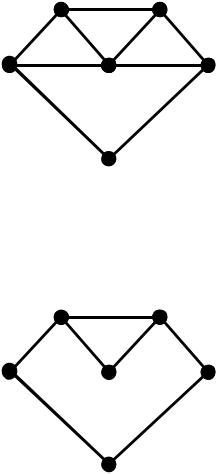
Граф, у якого = 2, називається біхроматичним (біграф).

Теорема Кеніга (критерій дводольності графа)

Непустий граф є біхроматичним тоді й тільки тоді,

коли він не містить циклів непарної довжини

Доведення.

1) Достатність.

Дано: граф G не містить циклів непарної довжини.

Довести: граф G є біхроматичним, тобто (G) .

Візьмемо довільну вершину u графа G, офарбимо її в колір 1, всі суміжні їй вершини офарбимо в колір 2, всі суміжні з вершинами, пофарбованими в колір 2 – офарбимо в колір 1 і так далі. При цьому ніяка вершина не може бути пофарбована у два кольори.

230

Припустимо, що в результаті такого фарбування з'являється вершина, що повинна бути пофарбована двома кольорами. Нехай це вершина w .

Це означає, що вершини u і w з'єднані двома ланцюгами, причому одна з них має парну довжину, інша непарну.

Але тоді вершини u і w належать циклу непарної довжини, що суперечить умові теореми. Отже, будь-яка вершина графа розфарбована в перший або в другий колір, значить графа - біхроматичний.

2) Необхідність.

Дано: граф G – біхроматичний.

Довести: граф G не має циклів непарної довжини. Розфарбуємо вершини графа як і у випадку 1. Візьмемо довільний цикл z , що належить G .

У цьому випадку вершинні кольори 1 і 2 чергуються. Отже, кількість вершин циклу парна. Виходить, він має парну довжину.

Наслідок 1. Будь-яке дерево – біхроматично.

Наслідок 2. Будь-який дводольний граф є біхроматичним.

Задача про пошук хроматичного числа графа є NP-складною, тобто не існує ефективних поліноміальних алгоритмів для її рішення.

231

Алгоритм послідовного розфарбування

(субоптимальний, наближений, дає розфарбування близьке до мінімального)

1.Довільній вершині графа G приписуємо колір 1.

2.Нехай розфарбовані i вершин графа G у кольори від 1 до k , где k i . Довільній незабарвленій вершині приписуємо мінімальний колір

невикористаний при розфарбуванні суміжних з нею вершин.

Алгоритм послідовного розфарбування залежить від способу перебору вершин.

Наприклад.

Послідовність розфарбування така: (a, b, g, d, c, f) . Число красок, що використані для правильного розфарбування вершин графа дорівнює 4.

a f d

3

g

232

9.2.2 Розфарбування ребер

Нехай є G (V, E), де | V | p ,| E | q .

Реберним k-розфарбуванням графа G називається деяка функція , що задає відображення безлічі ребер графа G, у деяку k - елементну множину, тобто.

: E A {a1 ,a2 ,...,ak }.

Множина ребер, пофарбованих у певний колір, називають реберним однокольоровим класом.

Якщо (e) c , то говорять, що ребро e пофарбоване в колір c .

Реберне розфарбування є правильним, якщо суміжні ребра пофарбовані в різні кольори.

Граф у цьому випадку називається реберним k-розфарбованим. Мінімальне число k , при якому існує правильне реберне k -

розфарбування називається реберним хроматичним числом або хроматичним індексом.

Хроматичний індекс для повного графа з парним числом вершин дорівнює:

(K2n ) 2n 1 ,

і з непарним числом вершин:

(K2n 1 ) 2n 1.