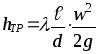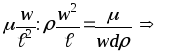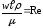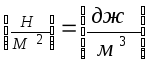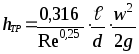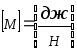9. Гідравлічні опори в трубопроводах

При русі в’язких рідин в трубопроводах і апаратах виникають спротиви, на долання яких витрачається енергія. Розрізняють два види гідравлічних опорів:

• супротив (опір) тертя;

• місцеві опори.

Опір тертя обумовлений силами тертя між рідиною і стінками трубопроводу і пропорційний довжині його. Його величина залежить від режиму руху рідини. При збільшенні турбулентності потоку збільшується турбулентна в’язкість рідини і, як наслідок, збільшується опір тертя.

Місцеві опори обумовлені створенням турбулентних вихорів в перерізах потоку, де швидкість рідини різко змінюється по величині або напряму.

Прикладами місцевих опорів являються:

раптове розширення потоку
раптове звуження потоку
відвід потоку під деяким кутом
засувки, вентиля і інші запиральні и регулюючі устрої

9.1. Витрати напору (тиску) на тертя при ламінарному режимі руху рідини

Розглянемо поток рідини в горизонтальному трубопроводі постійного перерізу

P₁ W₁ d P₂ W₂

1 ℓ 2

Хай d - діаметр трубопроводу;

ℓ - довжина трубопроводу;

P₁ i P₂ - тиск рідини в перерізах 1 і 2;

W - середня швидкість рідини .

Необхідно визначити залежність втрат тиску від геометричних розмірів трубопроводу, швидкості рідини і її властивостей, тобто ∆P_тр f (w, с, µ, ℓ, d).

Для ламінарного потоку ця задача може бути вирішена теоретичним шляхом.

У відповідність з рівнянням Бернуллі для реальної рідини

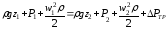
Так як Z₁=Z₂, w₁=w₂ = w, то ∆P_ТР = P₁ - P₂.

Значення P₁ - P₂ можна визначити з допомогою рівняння Пуазейля .

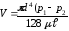Враховуючи, що 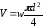, маємо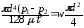, звідки

.

Позначимо 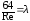- коефіцієнт опору тертя.

Тоді

		Розділивши це рівняння на ρg получимо
	[µ]	- втрата напору на подолання опору тертя.

Для каналів не круглого перетину коефіцієнт тертя ,де В – коефіцієнт, величина якого залежить від форми каналу.

Для квадратного перетину В = 57, для кільцевого перетину В= 96.

9.2. Втрати напору (тиску) на тертя при турбулентному режимі

руху рідини

Для розв’язання задачі скористаємось рівнянням руху в’язкої рідини, яка визначає розподіл швидкостей в потоці довільної форми. Так як це рівняння не може бути вирішено аналітичними методами, то знайдено його вирішення методом подібного перетворення у вигляді залежності між безрозмірними комплексами величин π₁ = f (π ₂, π _{3 …} π _n.

Для оси Z рівняння має вигляд:

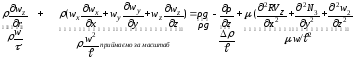зміна кількості сили інерції сили сили тиску сили тертя руху за 1 сек. тяготіння в 1 м³(накопичення)

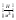
Вибравши в якості одиниці виміру (масштабу) сили інерції, розділимо почергово інші комплекси величин на масштаб:

1.	критерій гомохронності, що характеризує нестаціонарність процесу
	безрозмірний час, що характеризує фазу розвитку процесу
2.	критерій Фруда, що характеризує відношення сил тяготіння і інерції
3.	критерій Ейлера, що характеризує відношення сил тиску і інерції.
4.	критерій Рейнольдса характеризує співвідношення сил тертя і інерції.

Згідно другої теореми подібності вирішення рівняння Нав’є-Стокся можна представити у вигляді залежності між цими критеріями подібності:

, де 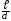- симплекс геометричної подібності

При вимушеному русі рідини під дією сил тиску впливом сил тяготіння можно знехтувати, тобто .

При усталеному (стаціонарному) русі критерій гомохронності перетворюється в константу і може не враховуватися.

Тоді

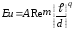
Шляхом обробки експериментальних даних про втрати тиску при русі в’язких рідин в гладких трубах знайдені величини:

А=0,158, m = - 0,25, q = 1

Eu=0,158 ·Re^-0,125 · або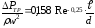

Позначимо -коефіцієнт тертя при турбулентному режимі руху.

Ця формула справедлива при значеннях 4000 < Re <100000.