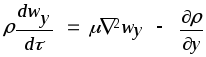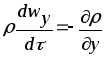- •Основи гідродинаміки
- •1. Сили, що діють на рідину в потоці
- •2. Основні параметри потоку рідини
- •3. Режими руху рідини
- •4. Закони ламінарного потоку
- •4.1. Закон розподілу швидкостей рідини в поперечному перерізі потоку
- •4.2. Витрата рідини в ламінарному протоці
- •4.3. Середня швидкість рідини в поперечному перерізі потоку
- •5. Характеристики турбулентного потоку
- •6. Закон збереження маси потоку Рівняння нерозривності потоку
- •8. Закон збереження енергії рідини рівняння Бернуллі
- •9. Гідравлічні опори в трубопроводах
- •9.1. Витрати напору (тиску) на тертя при ламінарному режимі руху рідини
- •9.2. Втрати напору (тиску) на тертя при турбулентному режимі
- •9.3. Вплив шорсткості (шершавості) на опір тертя
- •9.4. Втрати напору (тиску) на подолання місцевих опорів
- •10. Визначення оптимальної швидкості руху рідини і діаметра
6. Закон збереження маси потоку Рівняння нерозривності потоку
|
|
Розглянемо потік рідини в трубопроводі перемінного перерізу, який рухається без розривів, тобто без утворення пустот.
|
Хай S1 і S2 - площа перерізу 1 і 2 потоку;
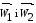 - швидкості
рідини в перерізах 1 і 2 (перемінні по
- швидкості
рідини в перерізах 1 і 2 (перемінні по
перерізу величини);
ρ1 і ρ2 - густина рідина в перерізах 1 і 2 (постійні по перерізу величини).
Необхідно визначити залежність між величиною поперечного перерізу трубопроводу і швидкістю рідини.
Складаємо баланс маси рідини для окресленого потоку.
Для
1 м3
потоку
баланс субстанції виражається основним
рівнянням переносу:

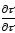 =
= -
-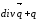 .
Потенціал переносу маси
.
Потенціал переносу маси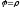 ,
щільність потоку маси
,
щільність потоку маси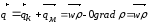 .
.
Після
підстановки цих величин в рівняння
переносу маємо:  =
=
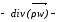 - дир. рівняння нерозривності потоку.
- дир. рівняння нерозривності потоку.
Для
усталеного потоку нестиглої рідини
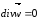 .
.
.
.
Проінтегруємо
рівняння
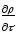 = -
= -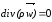 по усьому об’ємуокруглого
потоку:
по усьому об’ємуокруглого
потоку:
 .
.
Згідно теореми Гаусса-Остроградського
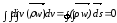 .
.
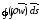 =
=
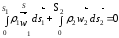
-
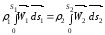
Оскільки
-
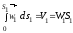 і
і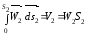 ,
то
,
то
|
ρ1 W1 S1 = ρ2 W2 S2 |
де V1 і V2 - об'ємна витрата рідини переріза 1:2; W1 і W1 – середня швидкість рідини в перерізах 1:2.
Таким чином, при нерозривному русі рідини масова витрата її є постійна величина вздовж усього потоку: G1 = G2 = G = const.
Для нестисної рідини ρ1 = ρ2 = ρ .
Тоді , тобто об'ємна витрата рідини постійна вздовж
W1 S1 = W2S2
V1 V2 усього потоку.
7. Закон збереження кількості руху
Рівняння руху в’язкості рідини
|
|
Виділимо
в потоці довільний об’єм рідіни.Хай
|
Необхідно визначити, як змінюється швидкість рідини в різних точках об’єму з часом, тобто знайти залежності:
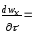 f1(х1
y1
z1
τ
),
f1(х1
y1
z1
τ
),
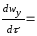 f2(
y2
z2
τ
),
f2(
y2
z2
τ
),
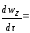 f3(
y3
z3
τ
)
f3(
y3
z3
τ
)
Для
цього складемо баланс проекцій кількості
руху на осі х, у, z. Для 1
м3
рідини рівняння балансу мають вигляд:
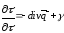 .
.
Для
осі Z:
α = ρwz,
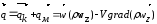
Щільність внутрішніх джерел кількості руху дорівнює сумі сил, що діють на 1 м3 рідини:

Тоді
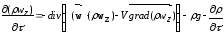
Вирішимо це рівняння для нестисної рідини.
Якщо ρ = const, то рівняння приймає вигляд
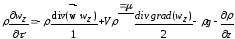
1.
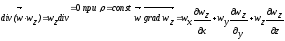
2.
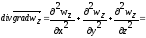 2
Wz
– оператор Лапласа
2
Wz
– оператор Лапласа
Тоді
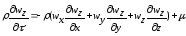 2Wz
–
2Wz
–
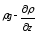

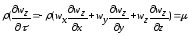 2Wz
–
2Wz
–
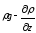
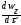 -
субстанційна похідна, тобто повна
похідна швидкість wz
по часу.
-
субстанційна похідна, тобто повна
похідна швидкість wz
по часу.
З урахуванням останнього маємо рівняння балансу проекцій кількості руху на вісі Z,X,Y:
|
сили інерції сили тертя сили тиску |
Диф.рівняння руху в’язкої нестисної рідини Навє-Стоксаю. Всі складові цих рівнянь мають розмірність сил, що діють на 1 м3 рідини. |
Фізичний сенс цих рівнянь:
|
Повна зміна за 1 сек. проекції кількості руху на будь яку вісь дорівнює сумі проекцій сил на цю вісь |
Для ідеальних рідин (µ=0) рівняння спрощується:
|
|
Рівняння руху ідеальної рідини (рівняння Ейлера) |