
- •Кафедра економіки і маркетингу курсова робота
- •Донецьк 2012
- •Реферат
- •1 Теоретичні основи використання статистичних методів при аналізі показників діяльності підприємств
- •2 Методологічні основи статистичного аналізу соціально-економічних явищ і процесів
- •3 Статистичний аналіз показників діяльності підприємства
- •3.2 Побудова економіко-математичної моделі для однофакторного зв'язку. Перевірка якості моделі.
- •Для знаходження b0та b1скористаймося формулами 2.15:
- •Для знаходження коефіцієнту детермінації скористаймося формулою 2.17:
1 Теоретичні основи використання статистичних методів при аналізі показників діяльності підприємств
1.1 Підготовка вихідних аналітичних даних. Засоби їх графічного представлення.
Будь-яке економіко-статистичне дослідження починається із статистичного спостереження. Статистичне спостереження - це попередня стадія статистичного дослідження, яка є планомірним, науково організованим обліком (збір) первинних статистичних даних про масові соціально-економічні явища і процеси.
Не всякий збір даних можна назвати статистичним спостереженням. Спостереження буде статистичним, по-перше, коли воно супроводжується реєстрацією фактів, що вивчаються, у відповідних облікових документах для подальшого їх узагальнення, по-друге - коли носить масовий характер. Це забезпечує обхват значного числа випадків прояву того або іншого процесу, необхідного і достатнього для того, щоб отримати дані, які стосуються не тільки окремих одиниць сукупності, але і всієї сукупності в цілому.
Збір статистичних даних може проводитися як органами державної статистики, науково-дослідними інститутами, іншими державними структурами, так і економічними службами банків, бірж, підприємств, фірм. Тільки в цьому випадку дослідники отримують достовірну і достатньо різноманітну статистичну інформацію, що дозволяє всесторонньо вивчати соціально-економічні явища.
Статистичне спостереження (збір первинного статистичного матеріалу) складається з трьох основних етапів:
підготовка статистичного спостереження;
організація і виробництво спостереження;
контроль отриманих первинних даних.
На етапі підготовки статистичного спостереження визначається мета, встановлюються об'єкт і одиниця спостереження, розробляються інструментарій і програма спостереження. Загальною метою статистичного спостереження є отримання достовірної інформації про тенденції розвитку явищ і процесів для подальшого ухвалення управлінських рішень. Вона повинна бути конкретною і чіткою. Нечітко поставлена мета може привести до збору не тих даних, які необхідні для вирішення конкретного завдання.
Мету визначає об'єкт статистичного спостереження. Об'єкт спостереження є деяка досліджувана статистична сукупність або фізичних осіб (населення, працівники), або юридичних осіб (підприємства, фірми, учбові заклади), або фізичних одиниць (виробниче устаткування, засоби пересування і транспортування, житлові будинки), тобто досліджувана статистична сукупність складається з окремих одиниць.
Одиниця спостереження - це первинний елемент об'єкту статистичного спостереження, який є носієм ознак, що підлягають реєстрації. Вказівка найважливіших ознак дозволяє встановити межі досліджуваної сукупності. Скажімо, якщо необхідно провести дослідження рентабельності поліграфічних підприємств, то необхідно визначити форми власності цих підприємств, організаційно-правові основи, кількість працівників підприємства, об'єм реалізації продукції, тобто те, що відрізняє як державні і недержавні підприємства, так і малі і крупні підприємства. Тільки в цьому випадку ми отримаємо достовірну статистичну інформацію.
Основною формою статистичного спостереження є звітність. Якщо первинний облік (первинний обліковий документ) реєструє різні факти, то звітність є узагальненням первинного обліку.
Звітність - офіційний документ, який скріпляється підписами осіб, відповідальних за надання і достовірність зібраних відомостей, і затверджується органами державної статистики. Окрім річної може мати місце щоденна, тижнева, двотижнева, місячна і квартальна звітність. Звітність може бути представлена поштою, телеграфу, телетайпу, факсу.
До спеціально організованого статистичного спостереження можна віднести перепис. На практиці проводиться перепис населення, матеріальних ресурсів, зелених насаджень, незавершених будівельних об'єктів, устаткування і так далі
Перепис - спостереження, що повторюється через рівні проміжки часу, завданням якого є не тільки визначення чисельності і складу досліджуваної сукупності, але і аналіз кількісних змін в період між двома обстеженнями. Зі всіх переписів найбільш відомі переписи населення.
Достатньо надійним джерелом даних є безпосереднє спостереження, коли можна встановити факт, що підлягає реєстрації. Але даний спосіб вимагає значних витрат праці і наявності всіх необхідних умов. Найчастіше він використовується при спостереженні за введенням в дію будівельних об'єктів.
Інший надійний спосіб - документальний, заснований на використанні як джерело інформації різних документів облікового характеру (рахунки, рекламації і так далі) і сприяючий отриманню точної інформації.
Спосіб спостереження, при якому джерелом відомостей є слова респондентів, називають опитом. Його різновиди: усний (експедиційний), анкетний, кореспондентський, явочний опит і саморегистрація.
Усний опит може бути як прямим (безпосереднє спілкування лічильника з респондентом), таким опосередкованим (наприклад, по телефону).
При анкетному способі певне число респондентів отримують спеціальні запитальники або особисто, або через засоби друку. Даний вид опиту застосовується в дослідженнях, де потрібні орієнтовні результати, що не претендують на високу точність (вивчення громадської думки).
Явочний спосіб використовується в суцільному спостереженні, коли необхідна особиста присутність (реєстрація браків, розлучень, народжень і так далі).
При кореспондентському способі відомості повідомляються штатом добровільних кореспондентів, через що отриманий матеріал не завжди носить якісний характер.
Нарешті, при способі саморегистрації формуляри заповнюються самими респондентами, а лічильники консультують і збирають формуляри. У статистичній практиці різні види статистичних спостережень можуть поєднуватися, доповнюючи один одного.
На третьому етапі зібраний статистичний матеріал повинен пройти контроль. Як показує практика, навіть при чітко організованому статистичному спостереженні зустрічаються погрішності і помилки, які вимагають виправлення. Тому метою цього етапу є як рахунковий, так і логічний контроль отриманих первинних даних. Розбіжність між розрахунковим і дійсним значеннями досліджуваної величини в статистиці називають помилкою спостереження. Залежно від причин виникнення розрізняють помилки реєстрації і помилки репрезентативності.
Помилки реєстрації можуть бути випадковими і систематичними. Випадкові помилки не мають певної спрямованості і виникають під дією випадкових чинників (перестановка цифр, зсув рядків і граф при заповненні статистичного формуляру).
Систематичні помилки реєстрації мають певну спрямованість, можуть або завищувати, або занижувати конкретне значення показника, що у результаті приводить до спотворення дійсного положення.
Для виявлення помилок використовується рахунковий контроль, особливо для перевірки підсумкових сум. Окрім рахункового використовується і логічний контроль, який може поставити під сумнів правильність отриманих даних, оскільки заснований на логічному взаємозв'язку між ознаками. Наприклад, при переписі населення отриманий факт, що п'ятирічна дитина має середню освіту, ставиться під сумнів і в цьому випадку ясно, що при заповненні формуляру допущена помилка.
Для подальшої обробки зібраних в ході статистичного спостереження первинних даних широко використовують і метод угрупування.
Угрупування - це розподіл безлічі одиниць досліджуваної сукупності по групах відповідно до істотної для даної групи ознаки. Метод угрупування дозволяє забезпечувати первинне узагальнення даних, уявлення їх в більш впорядкованому вигляді. Завдяки угрупуванню можна співвіднести звідні показники по сукупності в цілому із звідними показниками по групах. З'являється можливість порівнювати, аналізувати причини відмінностей між групами, вивчати взаємозв'язки між ознаками. Угрупування дозволяє робити вивід про структуру сукупності і про роль окремих груп цієї сукупності. Саме угрупування формує основу для подальшого зведення і аналізу даних.
Ознаки, по яких проводиться угрупування, називають группіровочнимі ознаками. Группіровочний ознаку іноді називають підставою угрупування. Правильний вибір істотної группіровочного ознаки дає можливість зробити науково обгрунтовані виводи за наслідками статистичного дослідження. Группіровочниє ознаки можуть мати як кількісний вираз (об'єм, дохід, курс валюти, вік і так далі), так і якісне (форма власності підприємства, пів людини, галузева приналежність, сімейний стан і так далі).
При визначенні числа груп, як правило, враховуються завдання дослідження, об'єм сукупності і види ознак, які беруться як підстава угрупування.
Метод типологічного угрупування полягає у виявленні в якісно різнорідній сукупності однорідних груп. При цьому дуже важливо правильно відібрати группіровочний ознаку, яка допоможе ідентифікувати вибраний тип. Типологічні угрупування широко застосовуються в дослідженні соціально економічних явищ. Прикладами такого виду угрупувань можуть бути групи підприємств по формах власності, по формах господарювання, соціальні групи населення і так далі У типологічних угрупуваннях часто використовуються спеціалізовані інтервали.
Метод структурного угрупування є розділення однорідної сукупності на групи за тією або іншою варіюючою группіровочному ознакою. На основі структурних змін вивчаються закономірності суспільних явищ
Метод аналітичного угрупування полягає в дослідженні взаємозв'язків між факторними ознаками в якісно однорідній сукупності. За допомогою аналітичних угрупувань вдається виявляти ознаки, які можуть виступати або причиною, або наслідком того або іншого явища. У аналітичних угрупуваннях найчастіше використовуються нерівні інтервали.
Результати группіровочного матеріалу оформляються у вигляді таблиць, де він висловлюється в наочно-раціональній формі. Не всяка таблиця може бути статистичною. Табличні форми календарів, тестових і опитних листів, таблиця множення не є статистичними.
Для зображення статистичних рядів розподілу використовують такі графіки:
полігон,
гістограма,
кумулята і огіва,
Полігон – зображення варіаційного (переважно дискретного) ряду у вигляді ламаної лінії, що з’єднує сукупність точок в прямокутній системі координат. Значення ознаки відкладається на осі абсцис (Х), а частоти (частки, щільність) – на осі ординат (Y).
Гістограма – сходинковий графік для інтервального варіаційного ряду. Утворені прямокутники пропорційні за висотою частотам варіантів для кожного інтервалу. У випадку нерівних інтервалів висота прямокутників пропорційна щільності розподілу ознаки у конкретному інтервалі. Гістограму можна перетворити на полігон, з’єднавши середини вершин стовпчиків лінією. За гістограмою зручно визначати модальне значення ознаки – праву верхню вершину модального (з максимальною ординатою) прямокутника з’єднуємо з правою вершиною попереднього, а ліву вершину модального прямокутника – з лівою вершиною після модального прямокутника. Абсциса точки перетину з’єднувальних прямих буде модою розподілу.
Кумулята і огіва – криві нагромаджених (кумулятивних) підсумків частот або часток. Використовують для зображення як дискретних так і інтервальних рядів. Будуючи кумуляту, на абсцисі відкладають варіанти, на ординаті – нагромаджені частоти. У разі побудови огіви, яка є дзеркальним відображенням кумуляти, навпаки. За цими кривими визначають, скільки одиниць сукупності, або яка їх частка не перевищує певного значення групувальної ознаки (для дискретного ряду) чи верхньої межі відповідного інтервалу (для інтервального ряду). Кумулятивні криві надають можливість графічного визначення медіани – остання ордината кумуляти ділиться навпіл і через середину проводиться пряма паралельно осі абсцис до перетину з кривою. Значення абсциси цього перетину є медіаною.
1.2. Використання середніх величин та характеристик варіації при аналізі економічних показників.
Статистичне дослідження незалежно від його мети та масштабів завжди завершується розрахунком та аналізом різних за видами та формою вираження статистичних показників. За допомогою статистичних показників створюється, передається та зберігається інформація про розміри, пропорції, зміни в часі та інші закономірності досліджуваних явищ.
Показники, які статистично характеризують досліджувану сукупність в цілому чи її окремі частини, називають узагальнювальними і розрізняють за способом обчислення (первинні та похідні), ознакою часу (інтервальні та моментні) та аналітичними функціями.
Узагальнювальні показники можуть бути представлені:
абсолютними,
відносними,
середніми величинами.
Середня величина – узагальнювальний показник, який характеризує типовий рівень варіюючої ознаки, в розрахунку на одиницю однорідної сукупності і може не збігатися з жодним з індивідуальних значень ознаки. Виражається у одиницях виміру ознаки.
Середня буде надійною і характеризуватиме типовий рівень ознаки лише за умови, що сукупність якісно однорідна.
Важлива властивість середньої полягає в тому, що в ній взаємно компенсуються індивідуальні відмінності елементів, які зумовлені дією випадкових факторів і узагальнюються типові риси.
Залежно від особливостей досліджень та характеру вихідних даних, а також певної математичної дії над емпіричними значеннями ознаки (підсумовування, множення, коренювання, степенювання) застосовують відповідний вид середніх величин.
Усі види середніх поділяють на два класи:
степеневі середні – середня арифметична, середня гармонійна, середня геометрична, середня квадратична; кожна може бути проста і зважена;
структурні (позиційні) середні – мода і медіана.
Одним з найпоширеніших видів степеневих середніх у прикладній статистиці є середня арифметична, оскільки для більшості явищ характерна адитивність (підсумовування) обсягів (зарплата, витрати, виробництво, тираж, продаж тощо). Її застосовують при вивченні закономірностей розподілу, коли обсяг ознаки для всієї сукупності є сумою індивідуальних значень її окремих елементів.
Середня арифметична проста ( хсер ) обчислюється для незгрупованих даних таким чином: потрібно скласти всі індивідуальні значення ознаки ( х ) і суму поділити на їх кількість (n):
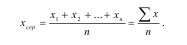
Середня арифметична зважена розраховується для згрупованих даних, коли відома частота повторення однакових значень ознаки (варіантів) у сукупності. Виконують такі операції: множення кожного варіанта ( х ) на його частоту ( ƒ ) – число, що вказує скільки разів цей варіант повторюється, підсумовування отриманих добутків і ділення суми на суму частот:

де процес множення ( хƒ ) – називають зважуванням, що відображує факт рівновагомості окремих варіант, а частоту ( ƒ ) – вагою варіанти.
Важливо відмітити, що на значення середньої вливає коливання структури сукупності. Чим більшу вагу мають великі значення ознаки, тим більша середня, і навпаки, що видно з наведеного вище прикладу. На цю властивість середніх слід зважати при використанні їх у порівняльному аналізі.
Якщо варіанти ознаки подаються у вигляді інтервалу (від..до), то слід знайти серединне значення кожного з інтервалів як півсуму двох меж.
При обчисленні середньої з відносних величин (середній процент, середня питома вага) необхідно брати за ваги знаменники співвідношень, за допомогою яких були обчислені індивідуальні відносні показники.
У структурованій сукупності (складається з декількох груп) при розрахунку середньої зваженої варіантами є групові середні, кожна з яких має відповідну вагу у вигляді групових частот. Обчислену таким способом середню називають загальною.
Основні властивості середньої арифметичної:
алгебраїчна сума відхилень усіх варіантів від середньої дорівнює нулю:
![]()
отже в середній взаємно компенсуються додатні та від′ємні відхилення окремих варіант;
сума квадратів відхилень варіантів від середньої менша за будь-яку іншу величину:
![]()
якщо частоти всіх варіантів поділити чи помножити на будь-яке число, то середня від цього не зміниться:
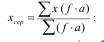
тому величина середньої залежить не від абсолютних значень ваг, а від пропорцій між ними, від питомої ваги варіанта в сукупності; Згідно з цією властивістю замість абсолютних ваг – частот ( ƒ ) – можна використати відносні ваги у вигляді часток ( d ).
Інші степеневі середні використовують рідше. Середню гармонійну – як обернену середній арифметичній, застосовують тоді, коли чисельність сукупності невідома. Середню геометричну – для аналізу рядів динаміки. Середню квадратичну – при розрахунках абсолютних і відносних показників варіації ознаки.
Структурним середнім надають перевагу в умовах недостатньої кількості вихідних даних (наприклад, обмеження інформації у зв’язку з “комерційною таємницею”), а також для більш детального розкриття властивостей розподілу і характеристики структури досліджуваної сукупності.
У середніх узагальнювальних показниках, якими є степеневі середні, не видно ні найбільш визначних досягнень, ні відставань, оскільки середня нівелює (стирає, ігнорує) усі індивідуальні особливості. Тому їх доповнюють особливими показниками – модою та медіаною, які є конкретними описовими характеристиками статистичного ряду. Ці характеристики завжди відповідають повному варіанту.
Виражають показники варіації в абсолютних і відносних величинах.
До абсолютних показників належать:
розмах варіації;
середнє арифметичне відхилення;
дисперсія (середній квадрат відхилень);
середнє квадратичне відхилення.
Функції цих показників полягають у встановленні середньої величини з відхилень індивідуальних значень ознаки від їх середнього значення. Чим меншою є величина відхилень, тим краще, надійніше середній узагальнювальний показник характеризує сукупність.
Розмах варіації ( R ) є найпростішим з показників варіації і використовується для встановлення амплітуди варіаційної ознаки, тобто різниці між найбільшим і найменшим значенням ознаки:
R = xmax – xmin .
Середнє арифметичне (лінійне) відхилення ( dлін ) служить точнішою
характеристикою
варіації, оскільки враховує усі
відхилення ознаки від її середнього
значення. Обчислюється як частка від
ділення суми всіх відхилень на їх число.
Відхилення беруть за модулем, враховуючи
властивість середньої, що
![]() .
Отже:
.
Отже:
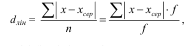
відповідно для незгрупованих та згрупованих даних.
Для більш об’єктивного оцінювання ступеня варіації при якому не порушуються закони алгебри щодо знаку відхилень (“ + ” чи “ – “) прийнято використовувати дисперсію (σ2) – показник середнього квадрата відхилень, міра розсіювання варіантів. Обчислюють аналогічно лінійному відхиленню з різницею у тому, що усі відхилення варіантів від середньої підносять у квадрат:

Види дисперсій:
загальна (σ2) – є результатом впливу усіх факторів, що спричинили варіацію ознаки, як постійних (систематичних), так і випадкових; характеризує варіацію ознаки навколо загальної середньої;
групова (часткова) (σі2) – є результатом впливу випадкових факторів (усіх крім фактора, покладеного в основу групування), характеризує варіацію ознаки у межах групи навколо групової середньої; узагальнюючою мірою внутрішньогрупової варіації є середня з групових дисперсій (σі2)сер;
міжгрупова дисперсія (δ2) – є результатом впливу фактора (постійного), який покладено в основу групування; характеризує відхилення групових середніх від загальної, тобто систематичну варіацію.
Між видами дисперсій існує співвідношення – правило складання дисперсій – загальна дисперсія дорівнює сумі середньої з групових дисперсій і міжгрупової дисперсії:
![]()
отже, чим більший внесок однієї з складових у загальну дисперсію, тим сильніший вплив відповідних їм факторів.
Це правило широко використовується при обчислюванні щільності зв′язку, у дисперсійному аналізі та в ряді інших випадків як для кількісних, так і для якісних ознак (дисперсія альтернативної ознаки дорівнює добутку частки одиниць, які мають цю ознаку, на частку одиниць, що її не мають). Наприклад, можемо дослідити, як впливає наявність спеціальної освіти на плинність кадрів (стаж), якість виконання роботи залежно від кваліфікації та інших умов, якість зберігання продуктів харчування залежно від терміну їх зберігання тощо. Тобто визначити який з факторів, що впливають на варіацію ознаки має більш (або менш) суттєве значення.
Середнє квадратичне (стандартне) відхилення (σ) – це квадратний корінь з дисперсії:
![]() .
.
Чим менше стандартне відхилення, тим повніше середня арифметична характеризує усю досліджувану сукупність, тим більш однорідною вона є.
Абсолютні показники варіації завжди виражаються у одиницях виміру ознаки.
Порівнюючи варіацію різних ознак в одній сукупності чи варіацію однієї ознаки в різних сукупностях, недостатньо виявити абсолютні величини варіації, оскільки вони залежать і від розміру варіації, і від рівня ознаки. Щоб забезпечити порівняння обчислюють відносні показники варіації, значення яких залежить від того, який саме абсолютний показник варіації використовується.
Базою порівняння служить середня арифметична величина ознаки (іноді медіана).
До відносних показників належать:
коефіцієнт осциляції (VR) – характеризує відносне коливання крайніх значень ознаки навколо середньої:

відносне лінійне відхилення (Vd):
![]()
коефіцієнт варіації (V) – найчастіше застосовується:
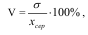
при V ≤ 33% сукупність є однорідною, а середня є типовою та надійною її характеристикою.
1.3 Статистичні методи вимірювання взаємозв'язків та їх роль у прогнозуванні економічних показників.
Метод аналітичного групування полягає у тому, що сукупність розбивається на групи за факторною ознакою (Х), далі по кожній групі та по сукупності визначаються середні значення Х та Y. Можна визначити показники співвідношення між приростами середніх за формулою:
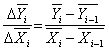 (1.1)
(1.1)
де ![]()
![]() -
середні значення факторної та
результативної ознаки по групах (групові
середні).
-
середні значення факторної та
результативної ознаки по групах (групові
середні).
Якщо
наведене співвідношення по групах
приблизно стале, між показниками існую
взаємозв'язок. Для оцінки тісноти
взаємозв'язку між ознаками визначається
емпіричне кореляційне відношення ![]() :
:
 (1.2)
(1.2)
де ![]() -
міжгрупова дисперсія результативної
ознаки;
-
міжгрупова дисперсія результативної
ознаки;
![]() -
загальна дисперсія результативної
ознаки;
-
загальна дисперсія результативної
ознаки;
![]() -
середня із внутрішньо групових дисперсій
результативної ознаки.
-
середня із внутрішньо групових дисперсій
результативної ознаки.
Емпіричне
кореляційне відношення змінюється в
межах від 0 до 1. Чим ближче його значення
наближається до 1, тим сильнішим є
взаємозв'язок між ознаками. При ![]() зв'язок
вважається функціональним. Крім цього,
визначається коефіцієнт детермінації
(D), який показує, на скільки відсотків
варіація Y зумовлена варіацією Х:
зв'язок
вважається функціональним. Крім цього,
визначається коефіцієнт детермінації
(D), який показує, на скільки відсотків
варіація Y зумовлена варіацією Х:
D= ![]() (1.3)
(1.3)
Для перевірки суттєвості взаємозв'язку між Х та Y часто використовують показник Фішера, який має назву F-критерія та визначається за формулою :
![]() (1.4)
(1.4)
де К2 = n-m, K1 = m-1 - число ступеней волі при кількості одиниць n та кількості груп m.
Критичні значення F-критерія для рівнів значимості 0,05 та 0,01 занесені у спеціальні таблиці. Із цих таблиць у відповідності зі значеннями К1 та К2 визначається так зване табличне значення F-критерія (Fтабл). Якщо виконується умова F>Fтабл , зв'язок між показниками можна вважати суттєвим, (невипадковим).
Стохастичні зв'язки, котрі характеризуються взаємодією середніх значень факторної та результативної ознак, називаються кореляційно-регресійними. Вони досліджуються з допомогою кореляційно-регресійного аналізу.
Найважливішою характеристикою кореляційного зв'язку є ліній регресії, тобто функція, котра пов'язує середні значення Х та Y . Кореляційно-регресійна модель взаємозв'язку являє собою рівняння регресії, яке у загальному вигляді записується наступним чином:
![]() (1.5)
(1.5)
де ух – теоретичні значення Y ;
![]() -
лінія регресії;
-
лінія регресії;
![]() -
залишкова компонента.
-
залишкова компонента.
У парному кореляційно-регресійному аналізі переважно використовуються наступні функції (рівняння регресії):
лінійна

параболічна
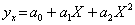
кубічна
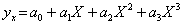
степенева

гіперболічна
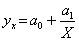
Метод побудови моделі такого зв'язку має назву багатофакторного кореляційно-регресійного.
Важливі умови побудови багатофакторної моделі зв'язку: достатня кількість одиниць у сукупності та відсутність мультиколінеарності факторів. Якщо два факторних показники мультиколінеарні, один з них повинен бути виключений з моделі.
На практиці використовуються два види рівнянь множинної регресії:
-
лінійне (адитивне): ![]()
-
нелінійне (мультиплікативне): ![]() ,
,
де а0, а1, а2, ... , аm – параметри рівняння множинної регресії;
Х1, Х2,Х3,. . ., Хm - факторні ознаки.
Оцінка параметрів рівняння множинної регресії здійснюється методом найменших квадратів. Параметри а1, а2 , . . . , аm називаються коефіцієнтами регресії та показують, на скільки одиниць змінюється у при збільшенні х на одиницю (якщо інші фактори є сталими). Наприклад, рівняння залежності ціни (Y) від рівня продуктивності праці (X1) та якості сировини (X2):
Ух = 12,3+9,5х1+4,2 х2 .
Для вимірювання тісноти взаємозв'язку між двома ознаками, що включені у модель, визначають парні коефіцієнти кореляції (ryx1, ryx2, rx1x2). Тісноту зв'язку між результативною ознакою (Y) та факторною характеризують часткові коефіцієнти кореляції (Ryx1, Ryx2).
Тісноту взаємозв'язку між результативною ознакою та сукупністю всіх факторних ознак визначають на основі коефіцієнта множинної кореляції R. Величина D = R2 називається коефіцієнтом детермінації, який показує, на скільки процентів варіація Y обумовлюється варіацією всіх факторних ознак у моделі.
Висновки по розділу 1
1. Статистичне спостереження - це планомірний, науково організований процес збирання даних щодо масових явищ і процесів, які відбуваються в різних сферах життя суспільства, шляхом їх реєстрації за спеціальною програмою, розробленою на основі статистичної методології.
Будь-яке статистичне дослідження послідовно проходить три етапи: перший етап - збір первинного матеріалу через реєстрацію фактів або опитування респондентів; другий етап - зібрані дані підлягають систематизації та групуванню: від характеристики окремих елементів переходять до узагальнених показників; третій етап передбачає аналіз варіації, динамік.
2. Середня величина є узагальнюючою мірою ознаки, що варіює, у статистичній сукупності. Середня дозволяє здійснювати порівняльний аналіз декількох сукупностей. У кожному конкретному випадку використовується певний вид середньої, зокрема: середня арифметична; середня гармонічна; середня геометрична; т. д. Залежно від характеру первинної інформації середня будь-якого виду може бути простою чи зваженою.
3. Метод аналітичного групування полягає у тому, що сукупність розбивається на групи за факторною ознакою (Х), далі по кожній групі та по сукупності визначаються середні значення Х та Y. Найважливішими умовами побудови багатофакторної моделі зв'язку є достатня кількість одиниць у сукупності та відсутність мультиколінеарності факторів. Тісноту взаємозв'язку між результативною ознакою та сукупністю всіх факторних ознак визначають на основі коефіцієнта множинної кореляції R. Величина D = R2 називається коефіцієнтом детермінації, що показує, на скільки процентів варіація Y обумовлюється варіацією всіх факторних ознак, включених у модель.
