1.1.2 Десятковий запис наближених чисел. Значуща цифра числа. Кількість вірних знаків

Будь яке десяткове наближення число а може бути наведено у вигляді

(1.8)

де – цифра числа, причому

–старший десятковий розряд числа .

Наприклад:

Значущою цифрою наближеного числа називається будь яка цифра в його десятковому зображенні, відмінна від нуля, і нуль, якщо він міститься між значущими цифрами або є представником збереженого десяткового розряду.

Наближене число а вигляду (1.8) містить n вірних значущих цифр у вузькому значенні, якщо абсолютна похибка цього числа не перевершує половини одиниці десяткового розряду, що виражається n-й значущою цифрою, рахуючи зліва направо, тобто якщо виконується нерівність

(1.9)

Наближене число а вигляду (1.8) містить n вірних значущих цифр в широкому значенні, якщо абсолютна похибка цього числа не перевершує одиниці десяткового розряду, виразимого n-ю значущою цифрою, якщо рахувати зліва направо, тобто якщо виконується нерівність

(1.10)

Приклад 1.2 Округлити число 1,2500 до двох значущих цифр.

Рішення.

Отримаємо наближене число 1,2 з абсолютною похибкою, що дорівнює

1.1.3 Зв'язок між кількістю вірних значущих цифр і похибкою числа

Якщо строгий підрахунок похибок не робиться, то можна приблизно оцінити за формулами

–у вузькому значенні (1.11)

–у широкому значенні. (1.12)

Приклад 1.3 Зі скількома десятковими знаками треба узяти , щоб відносна похибка була рівною 0,1%?

Рішення.

Оскільки перша цифра 4, то , та. Маємо, звідкиі.

1.1.4 Пряма і зворотна задачі теорії похибок

1.1.4.1 Пряма задача теорії похибок

Необхідно обчислити похибки даної функції, якщо відомі похибки аргументів.

З теорії похибок відомо, якщо була задана функція, що диференціюється і дані – абсолютні похибки аргументів, то з урахуванням виразу (1.2), гранична абсолютна похибка функції :

(1.13)

де - граничні абсолютні похибки аргументів функції .

За граничну відносну похибка функції можна прийняти:

(1.14)

Приклад 1.4 Знайти граничні абсолютну і відносну похибки об'єму кулі, якщо діаметрсмсм, а

Рішення.

Розглядаючи і як змінні величини, обчислюємо частинні похідні

Гранична абсолютна похибка об'єму:

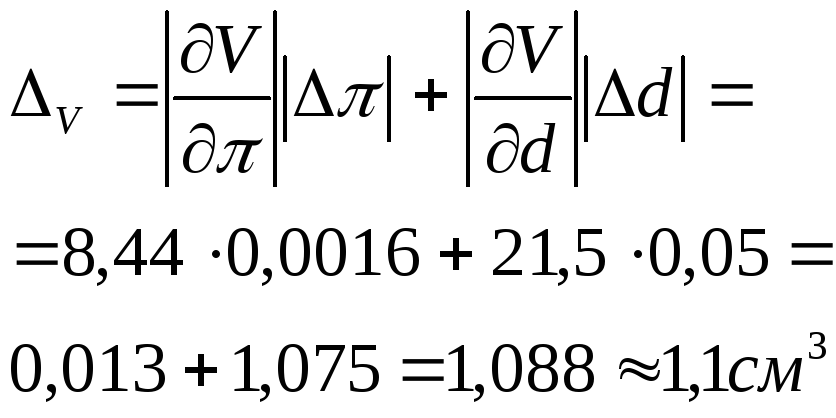
Тому

Звідки гранична відносна похибка об'єму

1.1.4.2 Зворотна задача теорії похибок

На практиці важлива також зворотна задача: які повинні бути абсолютні похибки аргументів функції, щоб абсолютна похибка функції не перевищувала заданої величини.

Ця задача математично невизначена, оскільки задану граничну похибка функціїможна забезпечити, встановлюючи по різному граничні абсолютні похибкиїї аргументів.

Найпростіше рішення отримуємо за принципом рівних впливів, тобто передбачається

Звідки

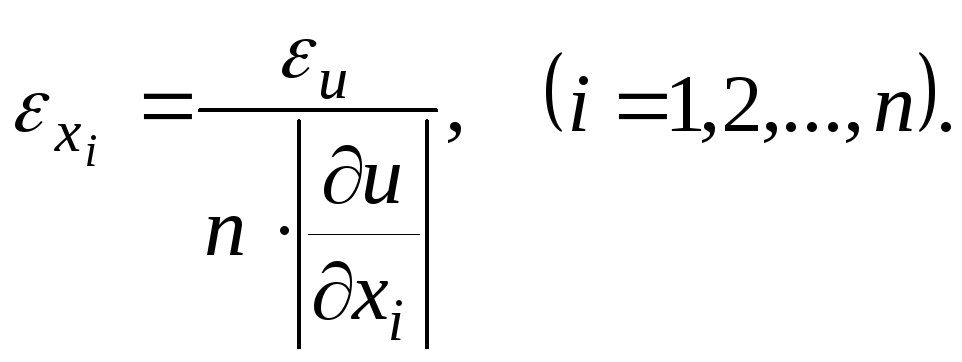(1.15)

Приклад 1.5 Радіус основи циліндра ; висота циліндра . З якими абсолютними похибками потрібно визначитиі, щоб об'єм можна було обчислити з точністю до?

Рішення.

Маємо і . Вважаючи ;;; приблизно отримаємо:

Отже