4.1.7 Комбінований метод дотичних і хорд

Характерна риса методів дотичних і хорд полягає в тому, що послідовності їхніх наближень монотонні. Причому, якщо для даного рівняння послідовність наближень методу хорд монотонно спадаюча, то послідовність наближень методу дотичних – монотонно зростаюча, і навпаки. Одночасне застосування цих методів дає можливість наближатися до кореня рівняння з двох сторін, одержуючи наближення з нестачею й надлишком.

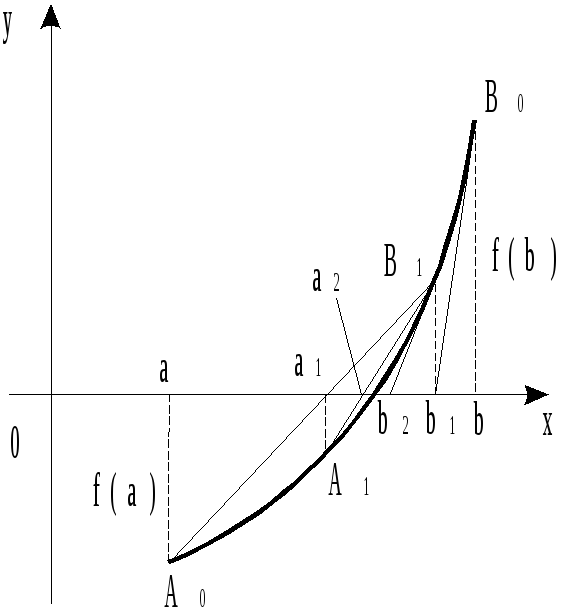
Рисунок 4.4 – Геометрична інтерпретація комбінованого методу

Розглянемо рівняння , корінь якого. Приймемо, наприклад,,,,(рис. 4.4).

У даному випадку за початкове наближення в методі хорд вибирають значення , а в методі дотичних – точку. На відрізкузастосовують метод дотичних і хорд (спочатку дотичних, а потім хорд). У результаті одержують нові наближення,, і початковий відрізок ізольованого кореня звужується. Для знаходження нових наближень застосовують метод дотичних і хорд уже на відрізку. У результаті одержують наближенняівідповідно, причому. Такий процес продовжують доти, поки довжина відрізкастане менше чи дорівнюватиме величині, де– наперед задана точність кореня.

За значення кореня , який шукається, беруть напівсуму наближеньі, тобто, а модуль їх напівсуми дає граничну абсолютну похибку наближеного кореня, тобто

.

Зауважимо, що на кожному кроці комбінованого методу за нерухомий кінець у формулі методу хорд потрібно брати наближення, обчислене на цьому ж кроці за формулою дотичних.

Формули комбінованого методу дотичних і хорд наведені нижче:

, , (4.8)

, (4.9)

За початкове наближення у формулі (4.8) методу дотичних беруть той з кінців відрізка, в якому значення функціїі її другої похідної мають однакові знаки, тоді протилежний кінець відрізкаберуть за початкове наближенняу формулі (4.9) методу хорд.

Завдяки своєрідній комбінації методів дотичних і хорд комбінований метод має більш високу швидкість збіжності, ніж методи хорд і дотичних окремо узяті.

4.2 Завдання на проведення лабораторної роботи

Варіанти завдань представлені в таблиці 4.1.

1) Відокремити корені заданого рівняння одним з методів: графічним, аналітичним чи методом послідовного перебору.

2) Уточнити один з відділених коренів рівняння двома, зазначеними в табл. 4.1, методами з точністю і.

3) Порівняти використані методи між собою за кількістю ітерацій, необхідних для знаходження кореня з заданою точністю.

4) Навести блок-схеми алгоритмів методів, які було використано в роботі.

Пояснення до виконання роботи. Виконуючи П.1 завдання, відрізок ізоляції кореня бажано звузити до довжини, що не перевищує одиниці.

При уточненні ізольованого кореня методом ітерації наведене в табл. 4.1 рівняння необхідно привести до виду , де функціяна відрізку ізоляції кореня повинна задовольняти умові.

Перед тим як використовувати методи хорд, дотичних і комбінований, необхідно перевірити достатні умови збіжності відповідного методу.

Таблиця 4.1 – Варіанти завдань

№	Рівняння	Метод
1		дихотомії, хорд
2		ітерації, комбінований
3		хорд, дотичних
4		дихотомії, хорд
5		хорд, Ньютона
6		дихотомії, комбінований
7		хорд, дихотомії
8		ітерації, хорд
9		дихотомії, комбінований
10		ітерації, комбінований
11		хорд, дотичних
12		хорд, Ньютона
13		ітерації, комбінований
14		хорд, дотичних
15		дихотомії, хорд
16		ітерації, комбінований
17		дихотомії, хорд
18		Ньютона, комбінований
19		ітерації, комбінований
20		хорд, дотичних
21		ітерації, хорд
22		дихотомії, комбінований
23		Ньютона, комбінований
24		хорд, дотичних
25		дихотомії, хорд
26		ітерації, комбінований
27		хорд, дотичних
28		дихотомії, комбінований
29		ітерації, комбінований
30		Ньютона, комбінований