2.2) Метод корреляционно-регрессионного анализа (рка)

Изучение корреляционной связи между признаками начинается с регрессионного анализа.

Регрессионный анализ позволяет выразить форму взаимосвязи между признаками с помощью уравнения регрессии и определить параметры уравнения регрессии.

Важной характеристикой корреляционной связи в методе (модели) корреляционно-регрессионного анализа (КРА) является теоретическая линия регрессии.

Теоретическая линия регрессии описывается определенной функцией (), которую называютуравнением регрессии, а () –теоретическим уровнем результативного признака.

Теоретическая линия регрессии в меньшей степени зависит от субъективизма исследователя, чем эмпирическая, однако, здесь так же может быть произвол при выборе формы (функции) взаимосвязи (уравнения регрессии). Считается, что выбор функции должен опираться на глубокое знание специфики предмета исследования.

Если анализируется зависимость между одним факторным и одним результативным признаками, то в этом случае имеем парную корреляционную связь и соответственно уравнение парной регрессии.

На практике чаще всего применяются следующие формы регрессионных моделей:

-	линейная
-	логарифмическая
-	гипербола
-	парабола второго порядка
-	показательная
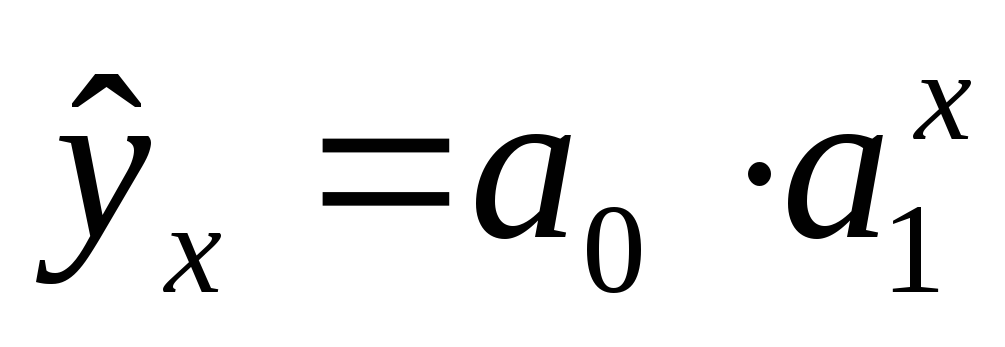
-	степенная

здесь а₀, а₁, а₂ – параметры уравнений регрессии, подлежащие определению.

Наибольшее распространение в экономико-статистических расчетах получила линейная форма регрессионной модели:

.

1.12

Параметры уравнения регрессии определяются методом наименьших квадратов, основное условие которого – минимизация суммы отклонений эмпирических значений (),от теоретических значений ():

.

(1.13)

Математически доказано, что значения параметров а₀ и а₁, при которых минимизируется сумма квадратов отклонений эмпирических значений результативного признака от его теоретических значений (1.12), определяются из системы нормальных линейных уравнений:

(1.14)

Решая эту систему, находим такие значения параметров:

;	(1.15)
.	(1.16)

Параметр а₀ – (свободный член уравнения регрессии) - характеризует теоретическое значение результативного признака () при нулевом значении факторного признака. Если границы вариации факторного признака () не содержат нуля, то этот параметр имеет только расчетное значение.

Параметр а₁ - (коэффициент регрессии) - характеризует на сколько единиц изменится результативный признак при изменении факторного признака на единицу.

В небольших по объему совокупностях коэффициент регрессиисклонен к случайным колебаниям. Поэтому следует проверить его истинность. Прилинейной связиистинность коэффициента регрессии проверяют при помощиt– критерия (критерия Стьюдента), величина которого определяется по формуле:

,

(1.17)

где стандартная ошибка коэффициента регрессии. Ее величина может быть определена по следующей формуле:

,

(1.18)

здесь - дисперсия факторного признака;

- остаточная дисперсия результативного признака;

- число степеней свободы;

- количество параметров уравнения регрессии. Для линейной функцииm=2.

Дисперсия факторного признака и остаточная дисперсия результативного признака могут быть определены по следующим формулам:

,	(1.19)
.	(1.20)

Полученное значение критерия Стьюдента () сравнивают с критическим значением (). Критическое значение принимается по таблицам в зависимости от уровня значимости () и числа степеней свободы ().

Таблица Значения квантилей t распределения Стьюдента при = 0,05.

Число степеней свободы	для критерия
	двухстороннего	одностороннего
4	2,78	2,13
5	2,57	2,01
6	2,45	1,94
7	2,38	1,89
8	2,31	1,86
10	2,23	1,81
15	2,13	1,75
20	2,09	1,73
30	2,04	1,70
	1,96	1,64

При соотношении > гипотеза о случайном характере коэффициента регрессии, отклоняется.

Для коэффициента регрессии, как и для любой другой случайной величины, определяются доверительные интервалы ().

Важной характеристикой регрессионной модели является относительный коэффициент влияния факторного признака (x) на результативный признак (y) – коэффициент эластичности (K_e):

.

(1.21)

Коэффициент эластичности показывает, на сколько процентов в среднем изменяется результативный признак (y) при изменении факторного признака на 1 %.

Корреляционный анализ используется для определения (1) тесноты и (2) существенности взаимосвязи между признаками.

1) Оценка тесноты корреляционных зависимостей дается после определения характера связи (расчета параметров уравнения регрессии) и эффекта влияния факторного признака на результативный признак.

Оценка тесноты связи или оценка согласованности вариации взаимосвязанных признаков позволяет установить количественную меру влияния факторного признака на результативный признак. Если влияние факторного признака на результативный значительное, то факторный признак своим влиянием формирует вариацию результативного. При отсутствии связи - вариация результативного признака не зависит от вариации факторного.

Для оценки тесноты связи в статистике используются целый ряд коэффициентов со следующими общими свойствами:

- при отсутствии какой-либо связи значение коэффициента приближается к нулю; при функциональной связи – к единице;

- при наличии корреляционной связи коэффициент выражается дробью, которая по абсолютной величине тем больше, чем теснее связь.

Для оценки тесноты линейной связи используют линейный коэффициент корреляции (r).

Вычисление линейного коэффициента корреляции базируется на отклонениях значений факторного и результативного признаков от их средних значений [(); ()] и осуществляется по формуле:

.

(1.22)

Интервал изменения линейного коэффициента корреляции:

- 1 + 1.

Для оценки тесноты связи можно воспользоваться следующей шкалой:

0,3	- связь между признаками слабая;
0,3 <0,6	- связь между признаками умеренная;
0,6 << 1,0	- связь между признаками тесная.

Коэффициент корреляции, оценивая тесноту связи, указывает также на ее направление:

- если связь прямая, коэффициент корреляции положительная величина;

- если связь обратная – отрицательная величина.

Знаки коэффициента корреляции и коэффициента регрессии одинаковы, а их величины связаны функционально (1.24).

На практике используют разные модификации приведенной формулы коэффициента корреляции. Приведем некоторые из них:

,	(1.23)
.	(1.24)

Измерение тесноты нелинейной связи базируется на соотношении вариаций теоретических и эмпирических (фактических) значений результативного признака. В регрессионном анализе это отклонения от линии регрессии () и отклонения линии регрессии от среднего из эмпирических значений результативного признака ().

Отклонения () являются следствием действия факторного признака (х), отклонения () – следствием действия других факторов. Взаимосвязь факторной и остаточной дисперсий описывается правилом сложения дисперсий:

.

(1.25)

где - общая дисперсия результативного признака;

- факторная дисперсия;

- остаточная дисперсия.

Эти дисперсии могут быть рассчитаны по формулам:

.	(1.26)
.	(1.27)
.	(1.28)

Очевидно, значения факторной дисперсии будет тем большим, чем сильнее влияние факторного признака на результативный. Отношение факторной дисперсии к общей рассматривается как мера тесноты корреляционной связи и называется коэффициентом детерминации:

.

(1.29)

Коэффициент детерминации показывает долю дисперсии результативного признака, которая объясняется выбранной регрессионной моделью.

Интервал изменения коэффициента детерминации - .

Чем ближе значение коэффициента детерминации к 1, тем лучше выбранная регрессионная модель объясняет эмпирические данные.

Вычисление и интерпретация коэффициента детерминации (R2) и корреляционного отношения () показывают – эти характеристики меры тесноты корреляционной связи по содержанию идентичны ихарактеризуют влияние факторного признака (x) на общую вариацию результативного признака (y).

Корень квадратный из коэффициента детерминации называют индексом корреляции (R) и используют для измерения тесноты связи между признаками:

.

(1.30)

Интервал изменения индекса корреляции - 01,0.

Для оценки тесноты связи можно воспользоваться следующей шкалой:

0 <0,3	- связь между признаками слабая;
0,3 <0,6	- связь между признаками умеренная;
0,6 << 1,0	- связь между признаками тесная.

При линейной связи между признаками – (). Исходя из этого по рассчитанному линейному коэффициенту корреляции можно определить влияние факторного признака на результативный признак. Так, приможно сказать, что 64 % вариации результативного признака зависит от вариации факторного признака.

2) После установления тесноты связи выполняется оценка существенности связи между признаками.

Порядок оценки существенности (истинности) связи:

1) Проверка истинности связи базируется на сравнении фактического (расчетного) значения коэффициента детерминации () с критическим значением ().

Критическое значение коэффициента детерминации () – это его максимальное значение при отсутствии связи между признаками

Критические значения () и () выбираются по таблице в зависимости от:

- факторной () или межгрупповой () дисперсии - ();

- числа степеней свободы остаточной () или средней из групповых () дисперсий - ();

- уровня значимости - ().

,

где n – число элементов статистической совокупности;

m – число факторных переменных уравнения регрессии. Для линейного уравнения т = 2.

Если при сравнении эмпирического и критического значений корреляционного отношения окажется:

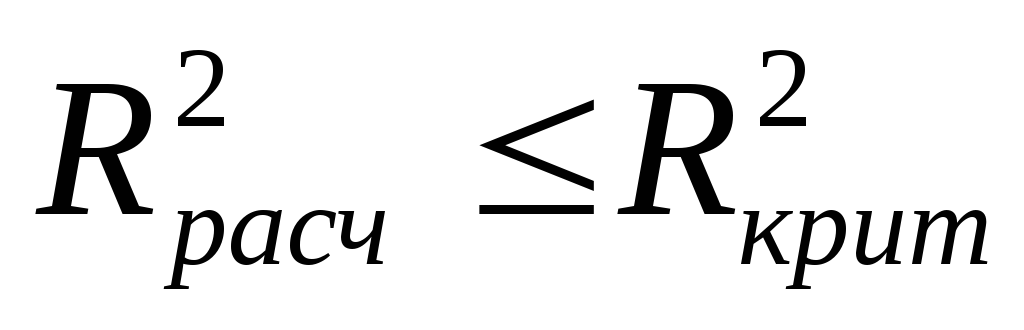
	- то установленная связь между признаками случайная;
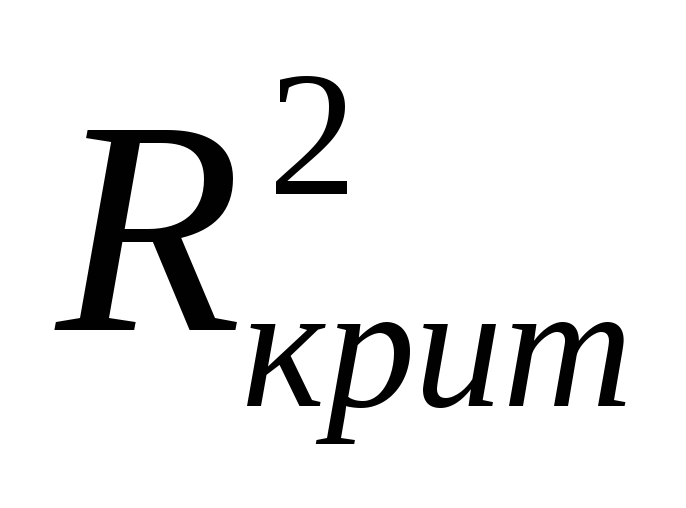
>	- то установленная связь между признаками существенная.

2) Проверка истинности связи может быть выполнена также с использованием F – критерия (критерия Фишера), который функционально связан с коэффициентом детерминации:

.

(1.31)

Порядок оценки истинности связи такой же – расчетное значение критерия Фишера () сравнивается с критическим значением () и по их соотношению делается соответствующий вывод:

	- то установленная связь между признаками случайная;
>	- то установленная связь между признаками существенная.
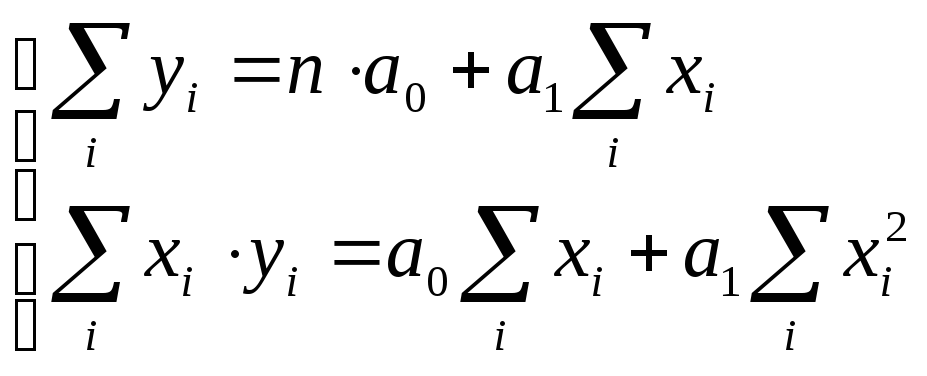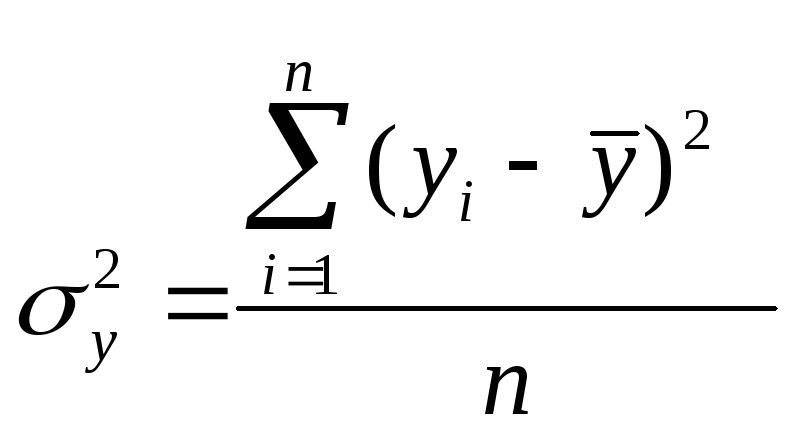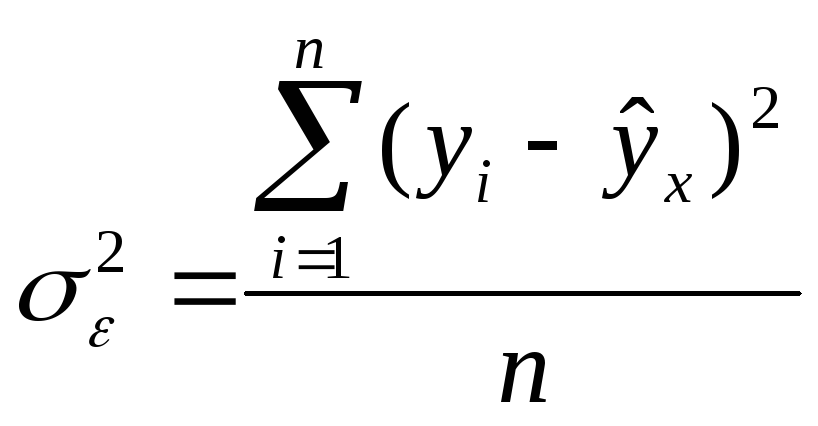