2. Индексный метод

Индексный метод изучения функциональных взаимосвязей будет рассмотрен в отдельной теме (тема «Статистические индексы»).

3. Статистические методы изучения стохастических связей

Основными методами изучения стохастических (вероятностных) связей являются:

1. метод параллельных рядов;

2. методы изучения корреляционных связей (метод аналитических группировок, метод КРА);

3. непараметрические методы изучения стохастических взаимосвязей.

1) Метод параллельных рядов

Метод параллельных рядов позволяет установить направление взаимосвязи между социально-экономическими явлениями путём сопоставления двух или более рядов показателей.

Сущность метода параллельных рядов заключается в следующем:

1. вначале показатели факторного признака располагаются в порядке возрастания или убывания, либо каждому факторному признаку присваивается определенный ранг (порядковый номер значения признака);

2. после этого параллельно значениям факторного признака или их рангам располагаются соответственно значения результативного признака или их ранги;

3. сравнение построенных таким образом рядов позволяет не только подтвердить наличие связи между признаками, но и выявить ее направление.

Для ориентировочной характеристики тесноты связи и ее направления в методе параллельных рядов используют:

1) в рядах представленных количественными признаками - коэффициент Фехнера.

Порядок определения коэффициента Фехнера:

1. Вычисляются средние значения факторного и результативного признаков - .

2. Для каждой пары определяется,, где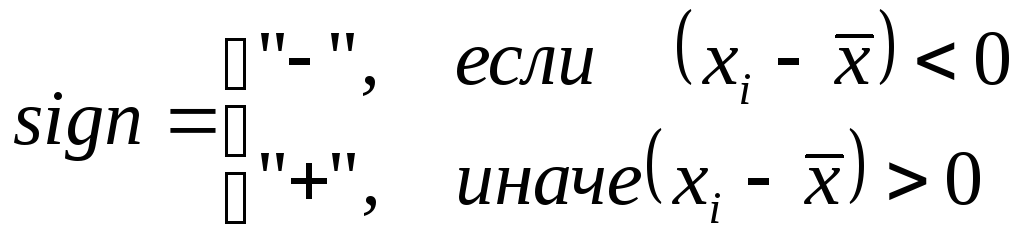

3. Расчёт ,

4. Расчет коэффициента Фехнера:

.

(1.3)

5. Определение тесноты и направления связи.

.

Если , то связь обратная,- связь отсутствует.

Если , то связь прямая,- связь функциональная.

Для качественной оценки тесноты связи можно воспользоваться соотношениями Чеддока:

	0	(0,1-0,3)	(0,3-0,5)	(0,5-0,7)	(0,7-0,9)	(0,9-0,99)	1,0
Сила связи	Отсутствует	Слабая	Умеренная	Заметная	Тесная	Весьма тесная	Функциональная

Или следующими интервалами коэффициента Фехнера:

0 <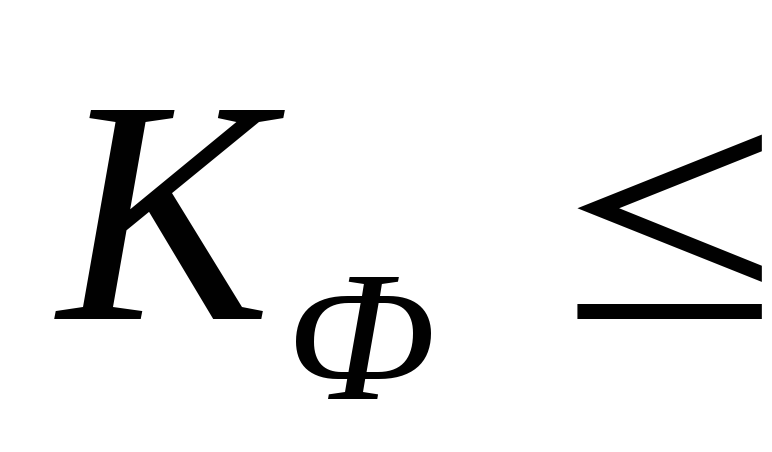0,3	- связь между признаками слабая;
0,3 <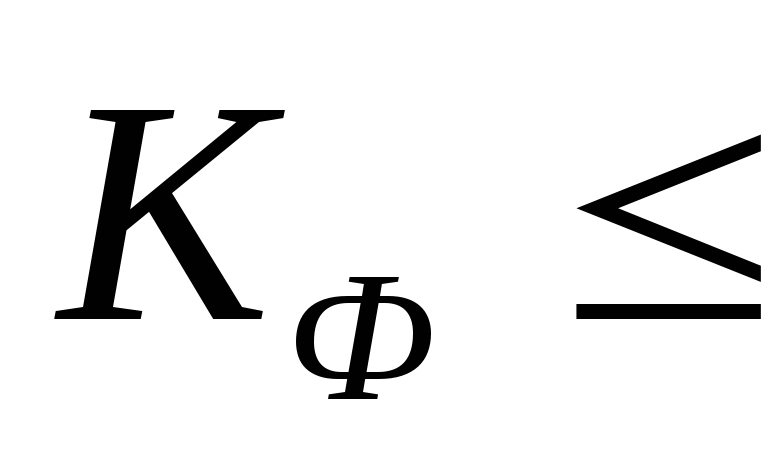0,6	- связь между признаками умеренная;
0,6 < <1,0	- связь между признаками тесная.

2) в рядах, представленных количественными или атрибутивными признаками, или количественным и атрибутивным признаками - коэффициент корреляции рангов (коэффициент Спирмена).

Порядок определения направления и тесноты связи с помощью коэффициента корреляции рангов (Спирмена):

1. Против каждого значения соответственно факторного и результативного признаков записываются их ранги ()(порядковые номера величин признаков). В случае наличия одинаковых значений признака каждому из них присваивается среднее арифметическое значение их рангов;

2. Определяется отклонение между рангами соответственно результативного и факторного признаков ;

3. Рассчитывается коэффициент корреляции рангов (Спирмена):

.

(1.4)

где n – количество единиц изучаемого ряда;

4. По величине коэффициента корреляции рангов определяют тесноту и направление связи между признаками.

.

Если , то связь обратная,- связь отсутствует.

Если , то связь прямая,- связь функциональная.

Для качественной оценки тесноты связи можно воспользоваться соотношениями Чеддока или следующими интервалами:

0 <0,3	- связь между признаками слабая;
0,3 <0,6	- связь между признаками умеренная;
0,6 < <1,0	- связь между признаками тесная.