2) Методы изучения корреляционных связей

Изучение корреляционной связи между признаками занимает значительное место в исследованиях социально-экономических явлений в экономике и управлению. Содержание такой связи составляет теория корреляции. Основоположниками этой теории являются английские ученые-биологи Ф. Гамильтон (1822 - 1911 гг.) и К. Пирсон (1857 - 1936 гг.).

Термин «корреляция» взят из природоведения и означает соотношение, соответствие.

С позиций математической статистики - корреляция – зависимость между случайными величинами, не имеющая строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.

Корреляционные связи в статистике изучаются методом аналитических группировок и методом корреляционно-регрессионного анализа (КРА).

В обоих случаях используется один и тот же подход. Вначале проводится регрессионный анализ, а затем – корреляционный анализ.

2.1) Метод аналитических группировок

Применение метода аналитических группировок начинается с регрессионного анализа, который позволяет установить эмпирическую линию регрессии.

Эмпирическая линия регрессии представлена групповыми средними результативного признака (), каждая из которых принадлежит соответствующему интервалу значений группировочного признака ().

Порядок определения эмпирической линии регрессии:

1. Определение факторного (Х) и результативного признака (У);

2. Определение средних значений факторного 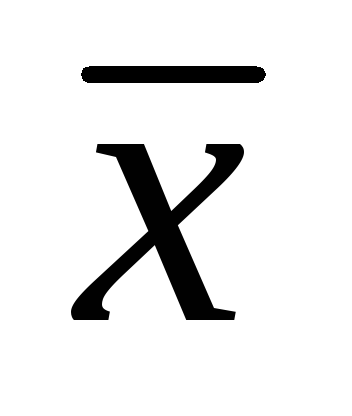и результативногопризнаков;

3. Группировка данных в соответствии с факторным признаком;

4. Определение среднего арифметического значения результативного признака 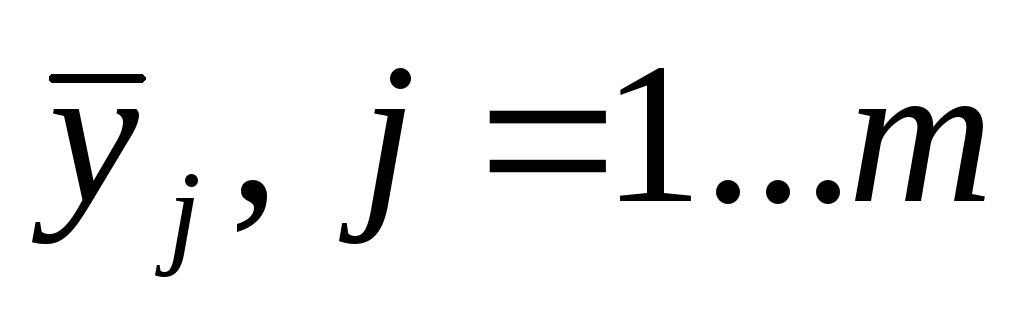для каждой группы;

5. Определение среднего арифметического значения факторного признака 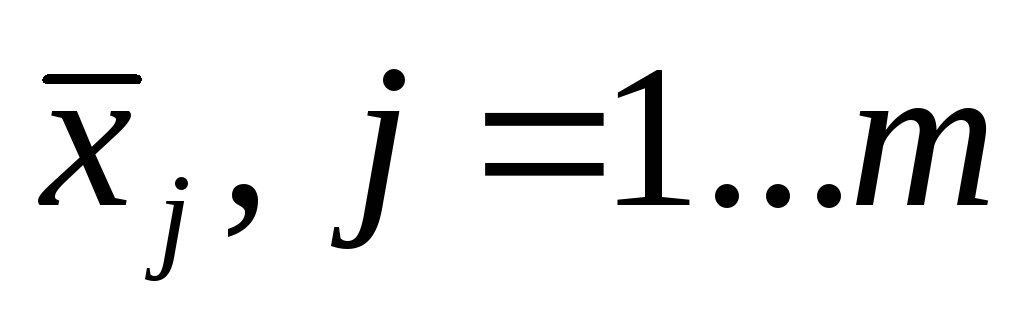для каждой группы;

6. Определение эмпирической линии регрессии (направления связи между признаками):

- если наблюдается одновременный рост (спад) средних внутригрупповых значений результативного и факторного признака, то связь прямая;

- если же наблюдается рост (спад) средних внутригрупповых значений результативного признака и спад (рост) средних внутригрупповых значений факторного признака, то связь обратная.

После определения эмпирической линии регрессии приступают к проведению корреляционного анализа. Корреляционный анализ используется для установления:

- тесноты связи между признаками;

- существенности связи между признаками.

Порядок определения тесноты связи между признаками:

1) Определение дисперсии результативного признака для каждой группы:

.

(1.5)

Внутригрупповые дисперсии показывают вариации результативного признака, вызванные всеми возможными факторами, кроме различий в значениях факторного признака;

2) Определение средней дисперсии из внутригрупповых дисперсий результативного признака:

.

(1.6)

3) Определение межгрупповой дисперсии результативного признака:

.

(1.7)

Межгрупповая дисперсия характеризует вариацию групповых средних результативного признака, обусловленную различиями между группами по факторному признаку;

4) Определение общей дисперсии результативного признака:

.

(1.8)

Общая дисперсия отражает суммарное влияние всех возможных факторов на общую вариацию результативного признака;

5) Определение корреляционного отношения:

.

(1.9)

Корреляционное отношение – показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния факторного признака на образование общей вариации результативного признака.

Интервал изменения корреляционного отношения: .

Чем ближе значение эмпирического коэффициента детерминации к 1, тем лучше модель объяснят эмпирические данные.

6) Определение индекса корреляции:

.

(1.10)

Индекс корреляции показывает тесноту связи между факторным и результативным признаками. Если значение индекса корреляции:

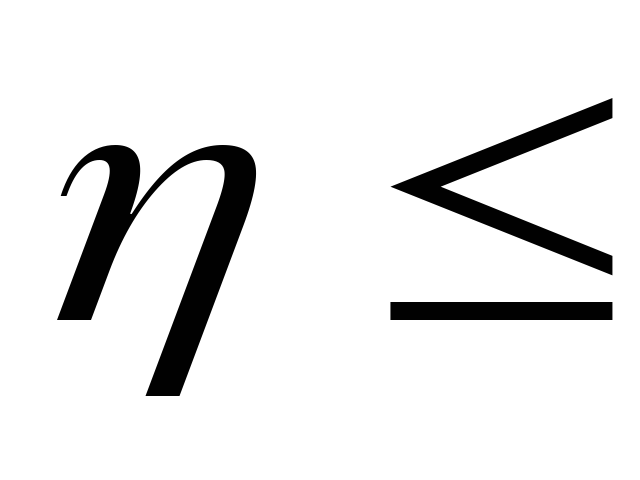0,3	- связь между признаками слабая;
0,3 <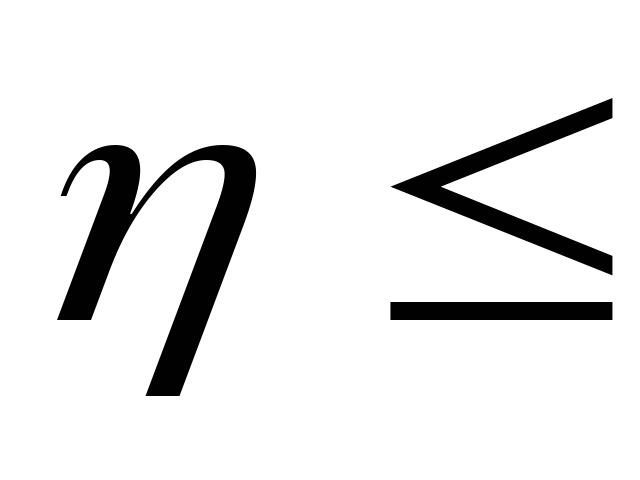0,6	- связь между признаками умеренная;
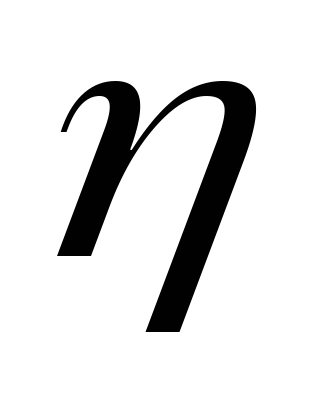> 0,6	- связь между признаками тесная.

Для качественной оценки тесноты связи на основе показателя индекса корреляции можно воспользоваться соотношениями Чеддока (см. метод параллельных рядов).

После установления тесноты связи необходимо выполнить оценку существенности связи между признаками. Под термином «существенность связи» понимают оценку отклонений эмпирических переменных от их значений в генеральной совокупности. Оценку существенности связи выполняют с помощью статистических критериев.

Порядок оценки существенности (истинности) связи:

1) Проверка истинности связи базируется на сравнении фактического (расчетного) значения корреляционного отношения () с критическим значением ().

Критическое значение корреляционного отношения – это его максимальное значение при отсутствии связи между признаками.

Критические значения выбираются по таблицам в зависимости от числа степеней свободы средней из групповых дисперсий (), межгрупповой дисперсии () и уровня значимости () – ().

,

где n – число элементов статистической совокупности;

m – число групп.

Если при сравнении эмпирического и критического значений корреляционного отношения окажется:

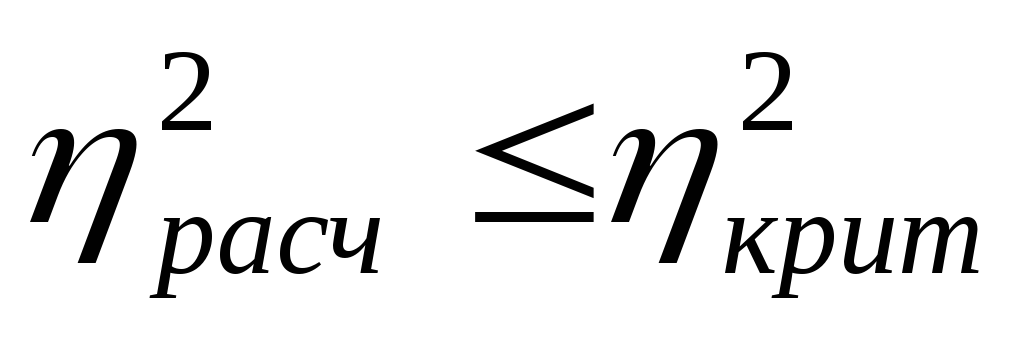
	- то установленная связь между признаками случайная;
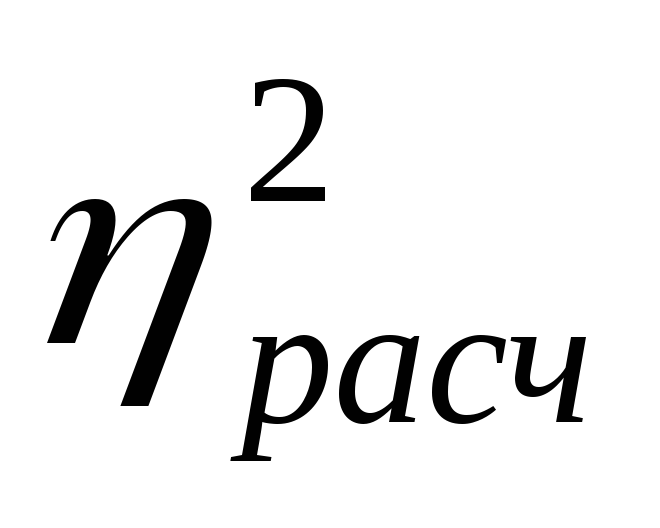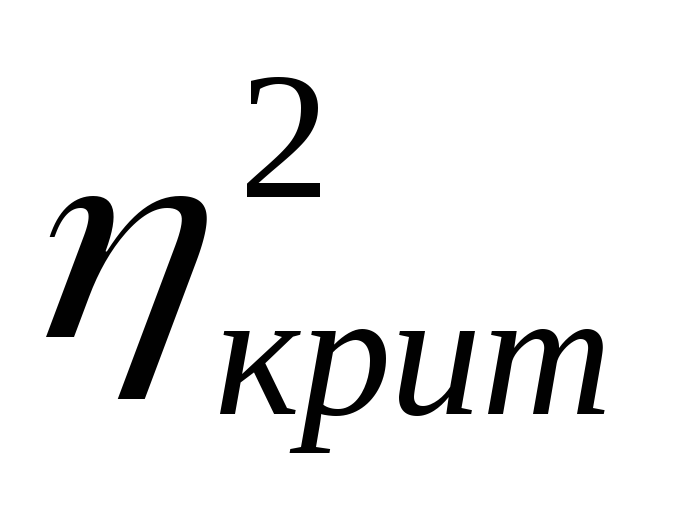
>	- то установленная связь между признаками существенная.

2) Проверка истинности связи может быть выполнена также с использованием F – критерия (критерия Фишера), который функционально связан с корреляционным отношением:

.

(1.11)

Порядок оценки истинности связи такой же – расчетное значение критерия Фишера сравнивается с критическим значением и по их соотношению делается вывод.
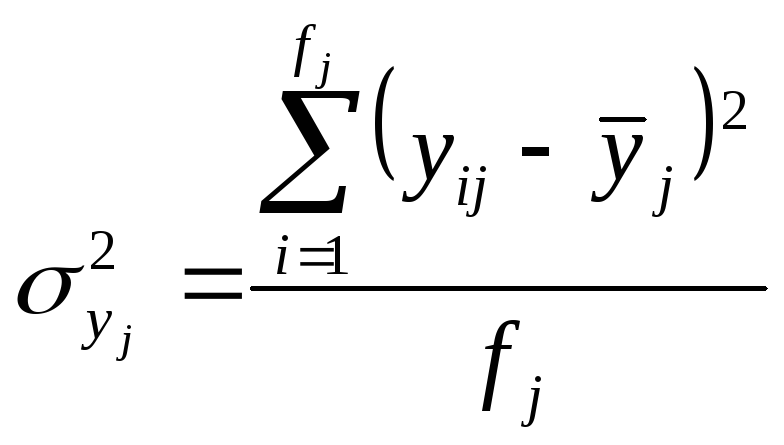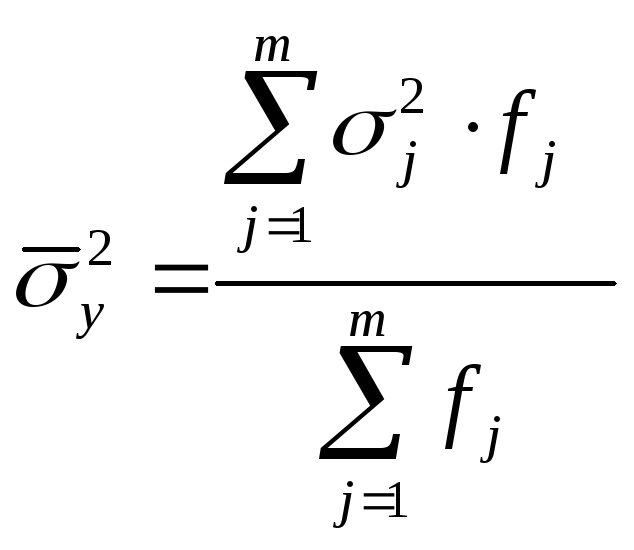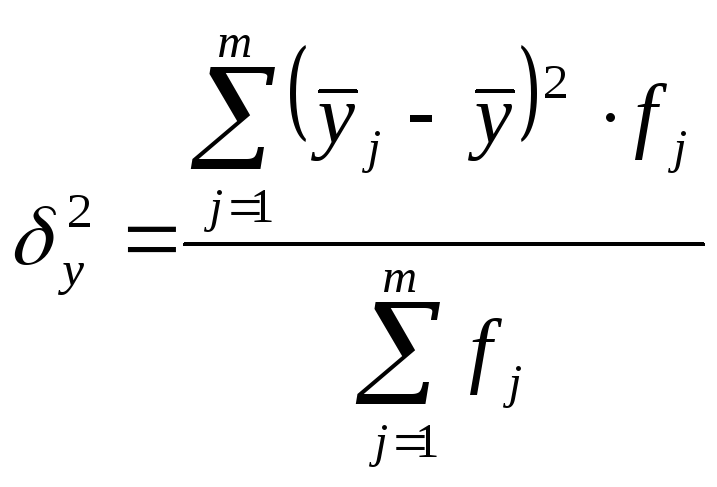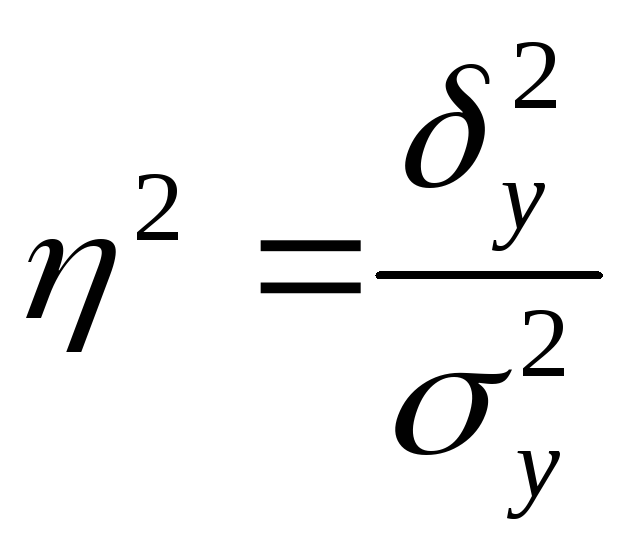