2.2 Рівняння тепловіддачі

За законом тепловіддачі щільність потоку тепла від стінки до рідини (або в зворотному напрямку) пропорційна різниці температур стінки і рідини.

q_к = (t_ст – t_рід).

Якщо q_к = const по всій поверхні стінки, то загальний потік тепла від стінки до рідини становить:

Q = q_кF = (t_ст – t_рід)F.

де  - коефіцієнт тепловіддачі, Вт/(м²град);

F – площа поверхні стінки, м².

Коефіцієнт тепловіддачі залежить від швидкості руху рідини вздовж стінки, її властивостей і геометричних розмірів потоку:

 = f(, , , С_р, , , l, d),

де  - температурний коефіцієнт об’ємного розширення рідини (м³/(м³град)), який відіграє значну роль при природній конвекції.

Теоретичним шляхом визначити  можна було б із умови рівності потоків тепла в межовому шарі за законом Фур’є і від стінки до рідини за законом тепловіддачі Ньютона:

де - градієнт температур в ламінарному шарі.

Для визначення градієнта температур необхідно знати розподіл температур в потоці, тобто функцію

2.3 Диференційне рівняння конвективного теплопереносу

Розподіл потенціалу переносу в системі описується основним рівнянням переносу:

Потенціал переносу тепла  = С_рt

Щільність потоку тепла

Якщо  = 0, то

Якщо  = const і С_р = const, то

– субстанціональна похідниця

Тоді – рівняння Фур’є-Кірхгора (дифрівняння конвективного теплопереносу).

Це рівняння повинно вирішуватись разом з рівняннями Нав’є-Стокса, нерозривності і межовими умовами. В загальному випадку ця система рівнянь не може бути вирішена аналітичними методами. Тому її рішення знаходять шляхом подібного перетворення диференційних рівнянь і знаходження залежності між безрозмірними комплексами величин.

2.4 Критерії теплової подібності

Виконаємо подібне перетворення диференційного рівняння конвективного теплопереносу:

накопичення тепла

Дж/м³с

конвективний теплоперенос, Дж/м³с

-масштаб молекулярний теплоперенос, Дж/м³с

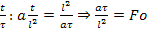1. – критерій Фур’є, що характеризує нестаціонарність процесу

– безрозмірний час

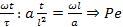2. – критерій Пекле, що характеризує співвідношення між інтенсивностями конвективного і молекулярного переносів тепла.

Замість критерію Пекле часто використовується похідний критерій, в який не входить швидкість:

Ре : Rе = - критерій Прандтля, характеризує подібність полів швидкостей і температур.

Він враховує вплив властивостей рідини на швидкість теплопереносу.

Критерії Fo і Ре (або Pr) є визначальними, оскільки в них входять тільки величини із умов однозначності. Визначаний критерій одержимо із умови теплообміну на межі тверда стінка-рідина, а саме із рівності молекулярного потоку тепла через межовий ламінарний шар (Закон Фур’є) і конвективного потоку тепла від стінки в ядро потоку рідини (закон тепловіддачі):

t

Масштаб

 t/l

Якщо за масштаб обрано молекулярний перенос тепла, то:

t : = Nu - критерій Нуссельта.

Nu = - відношення поперечного розміру потоку до товщини ламінарного межового шару.

У відповідності з другою теоремою подібності рішення диференційних рівнянь конвективного теплопереносу може бути представлено у вигляді функціональної залежності між знайденими безрозмірними комплексами величин:

Nu = f (Ho, Re, Fr, Fo, Pr, )

Для усталеного процесу Foconst, Нoconst. При вимушеній конвекції силами тяготіння (Fr) можно знехтувати. Тоді:

- критеріальне рівняння конвективного теплообміну при вимушеній конвекції.

Константи С, m, n, q визначають шляхом обробки експериментальних даних.

Наприклад, при турбулентному режимі руху рідини в прямій трубі при l/d  50 знайдено: C = 0,023, m = 0,8, n = 0,4, q = 0. Тобто:

При природній конвекції: Nu = f (Re, Fr, Pr, ).

Оскільки в критерії Re і Fr входить швидкість руху рідини, визначення якої при природній конвекції є складною задачею, то замість цих критеріїв використовують похідні критерії, в які не входить швидкість рідини.

Критерій Галіллея характеризує відношення сил тяжіння до сил тертя.

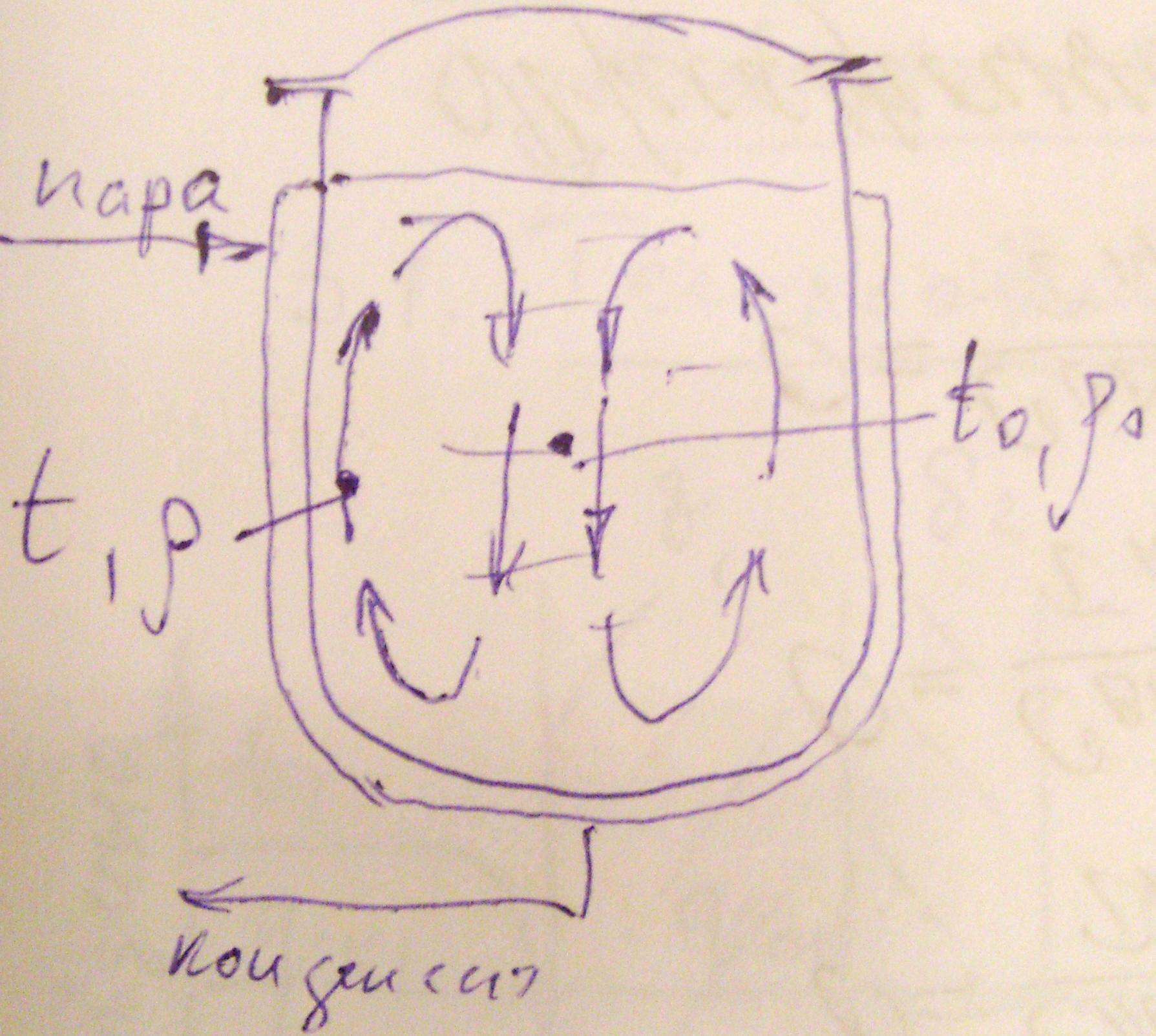
Рух рідини в представленому апараті обумовлений силами Архімеда, які становлять тільки частку сил тяжіння. Їх відношення до сил тертя називають критерієм Архімеда.

Якщо різниця густини рідини обумовлена різницею температур в різних точках, то:

₀ -  =  = ₀t,

де  - температурний коефіцієнт об’ємного розширення рідини, град^-1_. Тоді

- критерій Грасгофа

Всі величини, що входять в цей критерій легко визначаються при проведенні експериментів.

Критеріальне рівняння конвективного теплопереносу при природній конвекції має вигляд:

Можна бачити, що в цьому рівнянні критерій Gr заміняє критерій Re, тобто визначає вплив режиму руху рідини на інтенсивність теплопереносу.

3 Теплообмін між рідинами через стінку. Рівняння теплопередачі.

3.1 Теплообмін через пласку стінку

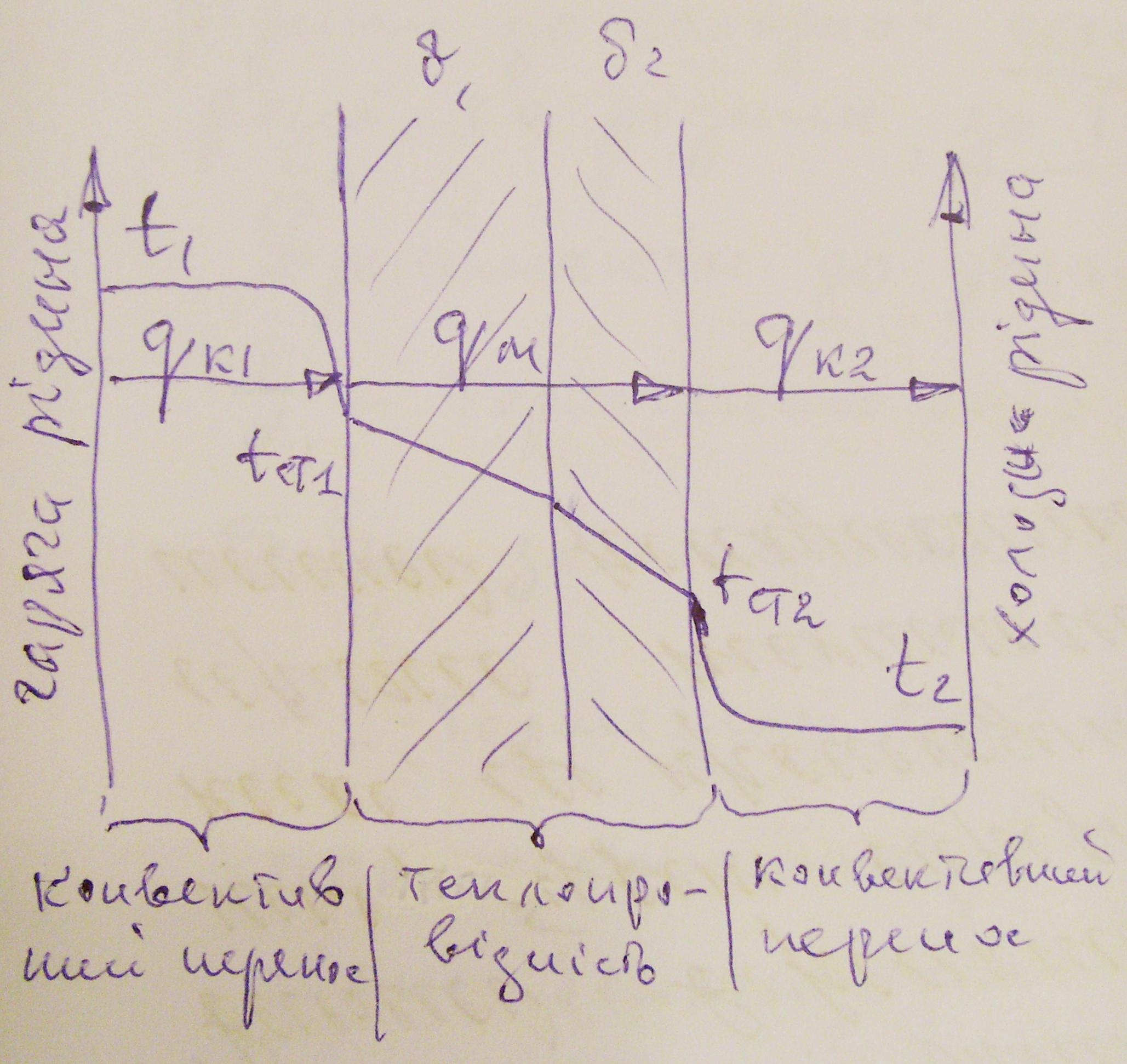
Розглянемо механізм переносу тепла від гарячої рідини до холодної.

Хай t₁ і t₂ – температура гарячої і холодної рідини;

₁ і ₂ – коефіцієнти тепловіддачі гарячої і холодної рідин;

₁ і ₂ – товщина шарів стінки;

₁ і ₂ - коефіцієнт теплопровідності шарів стінки.

Необхідно визначити щільність потоку тепла від гарячої рідини до холодної q.

Визначимо щільність потоку тепла на окремих ділянках системи:

q_к1 = ₁(t₁ – t_ст1) або q_к1 = (t₁ – t_ст1) (1)

q_к2 = ₂(t_ст2 – t₂) або q_к2 = (t_ст2 – t₂) (3)

При сталому процесі переносу тепла:

q_к1 = q_м = q_к2 = q

Склавши рівняння (1), (2,) (3) одержимо:

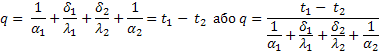
Позначимо тобто кількість тепла, що передається від гарячої рідини до холодної через 1 м² поверхні стінки, що розділяє рідини за 1 сек.

Приймаючи до уваги, що

- термічний опір гарячої рідини, ;

- загальний опір багатошарової стінки, ;

- термічний опір холодної рідини, ,

Можна констатувати, що К = , тобто коефіцієнт теплопередачі є обернена величина загального термічного опору системи. Таким чином щільність потоку тепла в даному перерізі q = К(t₁ – t₂) = Кt, а загальний потік тепла через стінку, площа поверхні якої F, становить:

Q = К(t₁ – t₂)_срF = Кt_ср F, Вт,

де t_ср = (t₁ – t₂)_ср – середнє значення рушійної сили теплопередачі в даному апараті.

В окремих випадках визначення коефіцієнта теплопередачі може спрощуватись.

Якщо .

Якщо , то К  ₁, а термічний опір називається визагальненим.

3.2 Теплообмін через циліндричну стінку

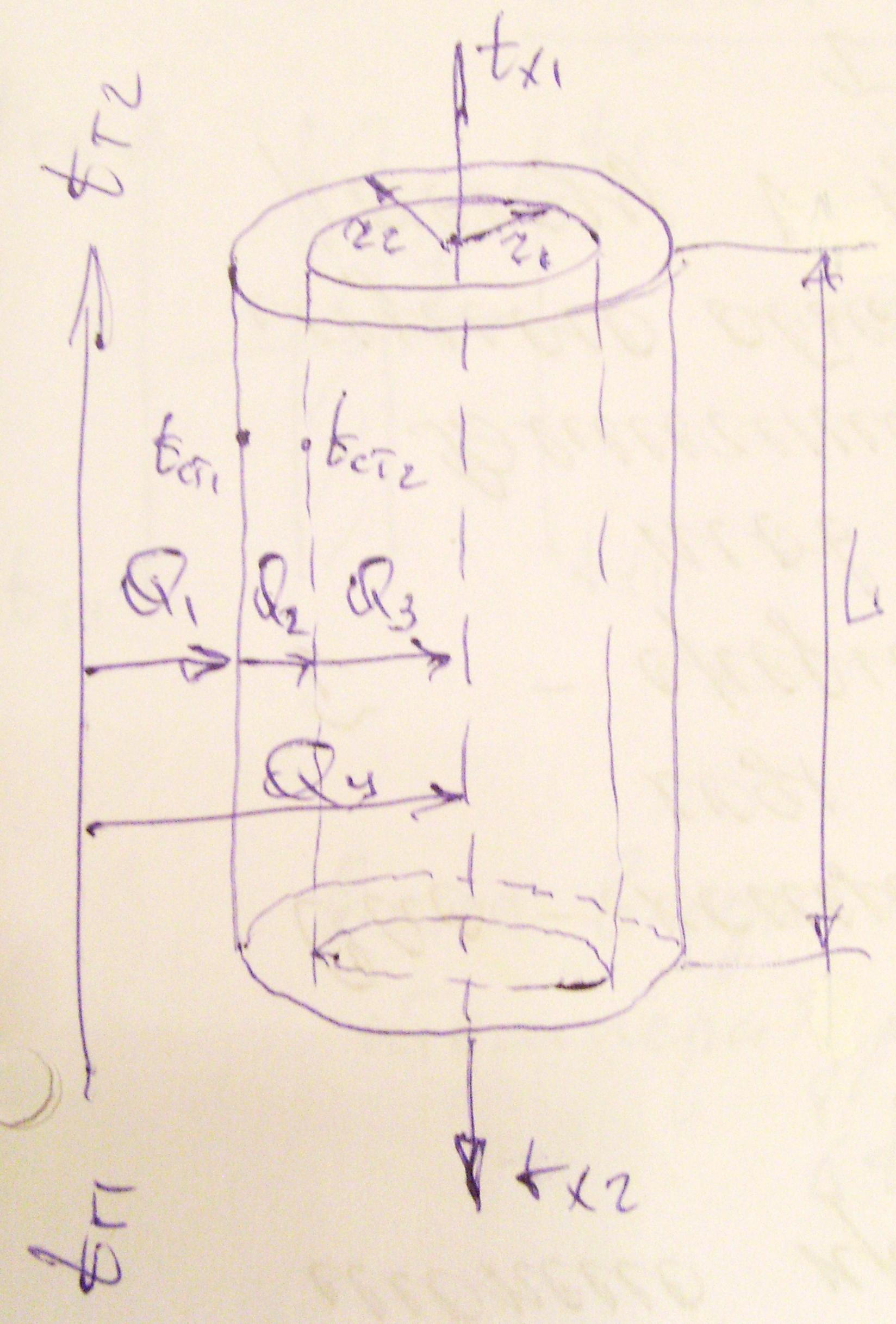
Визначимо потоки тепла на окремих ділянках системи:

Q₁ = ₁(t_г – t_ст1)_ср2r₁L

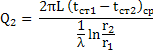
Q₃ = ₂(t_ст2 – t_х)_ср2r₂L

Вирішимо ці рівняння відносно рушійної сили на відповідних ділянках:

Для сталого процесу Q₁ = Q₂ = Q₃ = Q_ц.

Склавши рівняння (1), (2,) (3) одержимо:

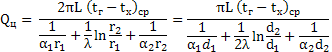
Позначимо - лінійний коефіцієнт теплопередачі, Вт/(мград), тоді Q_ц = К_L(t_г – t_х)_срL.

Якщо , то ,

де  = 0,5 (d₁ – d₂) – товщина стінки труби.

3.3 Визначення середньої різниці температур гарячої і холодної рідин

У більшості випадків температури гарячої і холодної рідин змінюються вздовж поверхні теплообміну, тобто по довжині теплообмінного апарату. Тому t = (t_г–t_х)=f, тобто рушійна сила теплопередачі є змінна вздовж поверхні теплопередачі. Вона визначається початковими і кінцевими температурами теплоносіїв і напрямком їх рухую

t_ср = f(t_г1, t_г2, t_х1, t_х2, схема руху теплоносіїв).

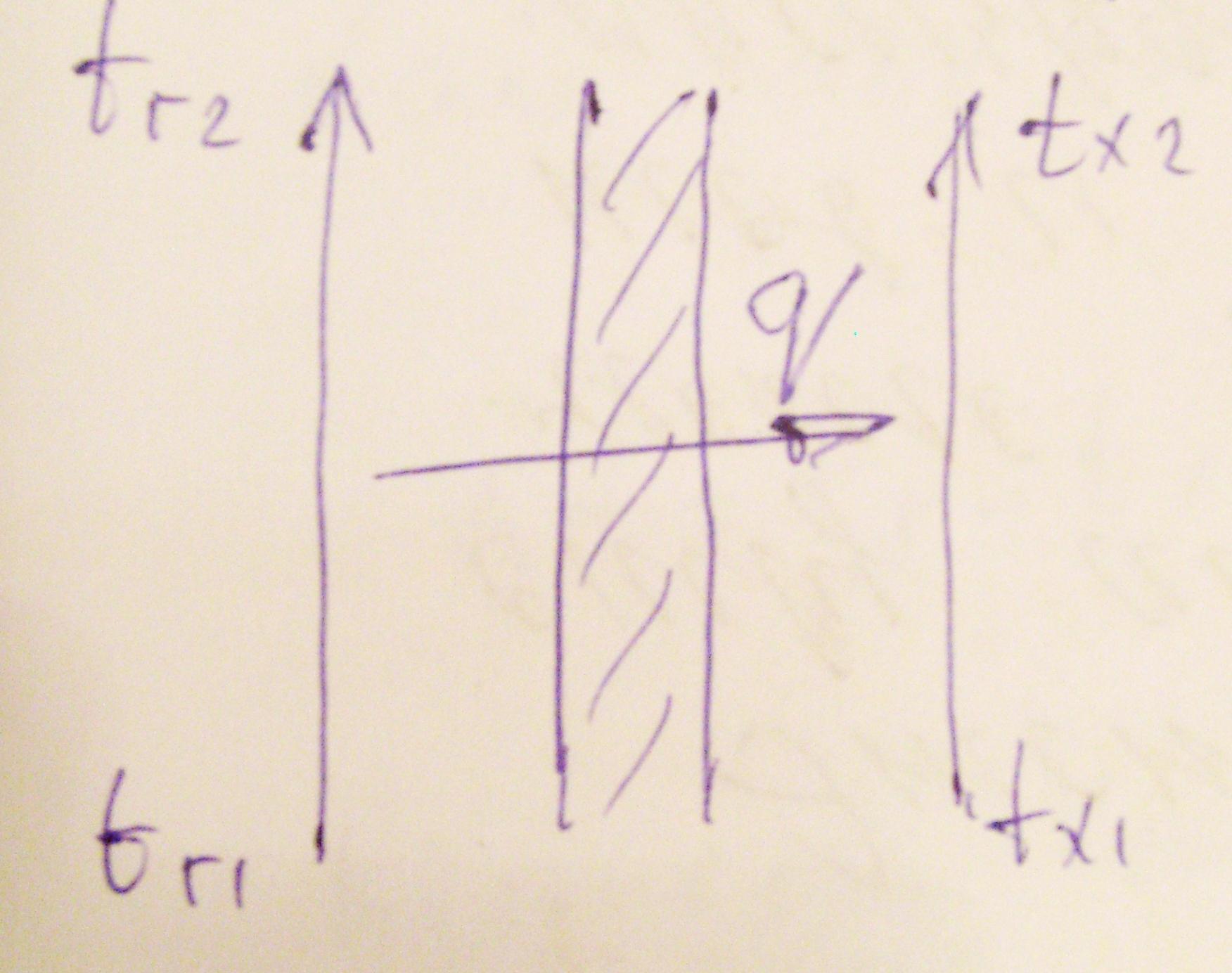
Існують різні схеми руху теплоносіїв:

• прямотік (паралельний тік)

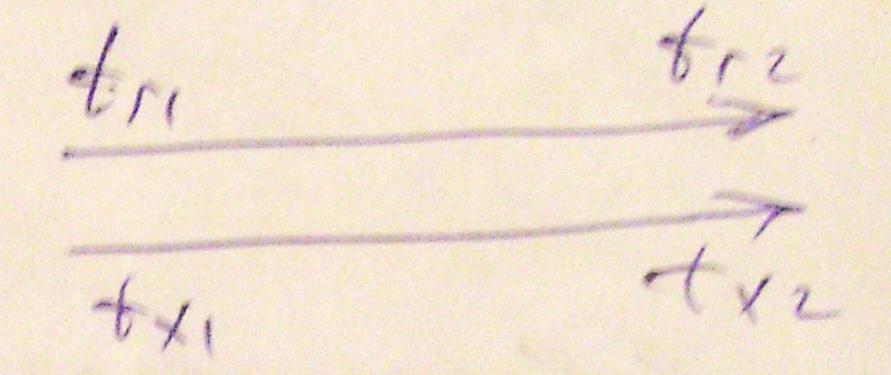
• протитік

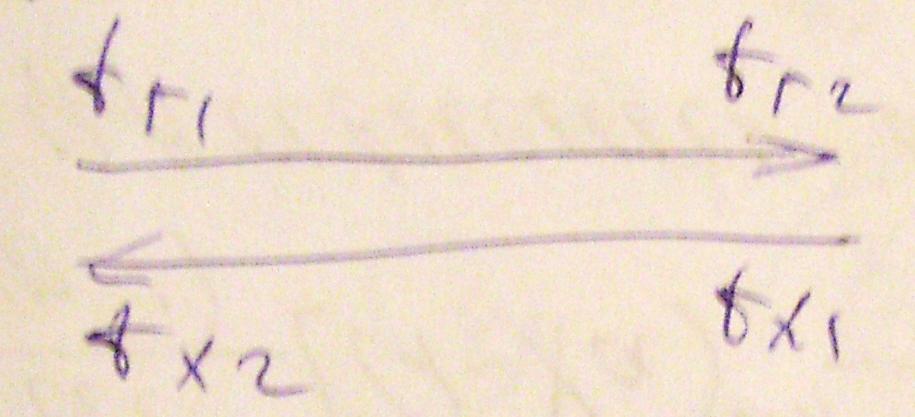
• перехресний тік

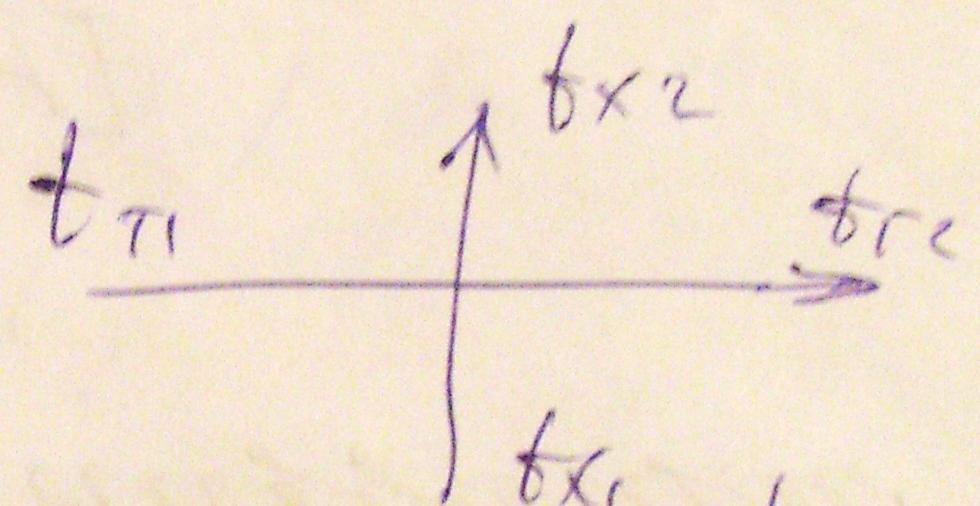
• змішаний тік

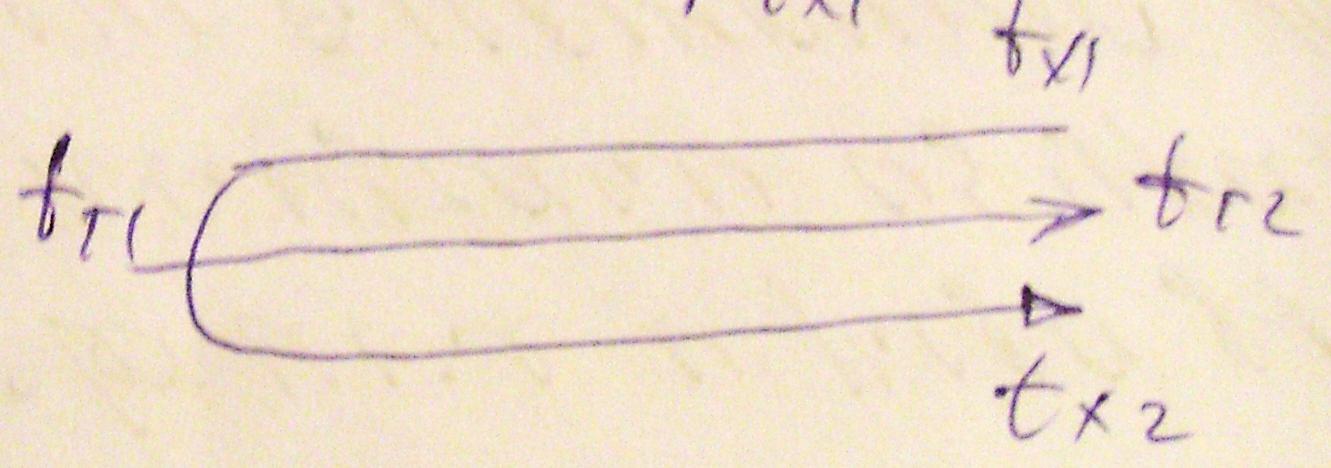
Визначення t_ср при прямотоці

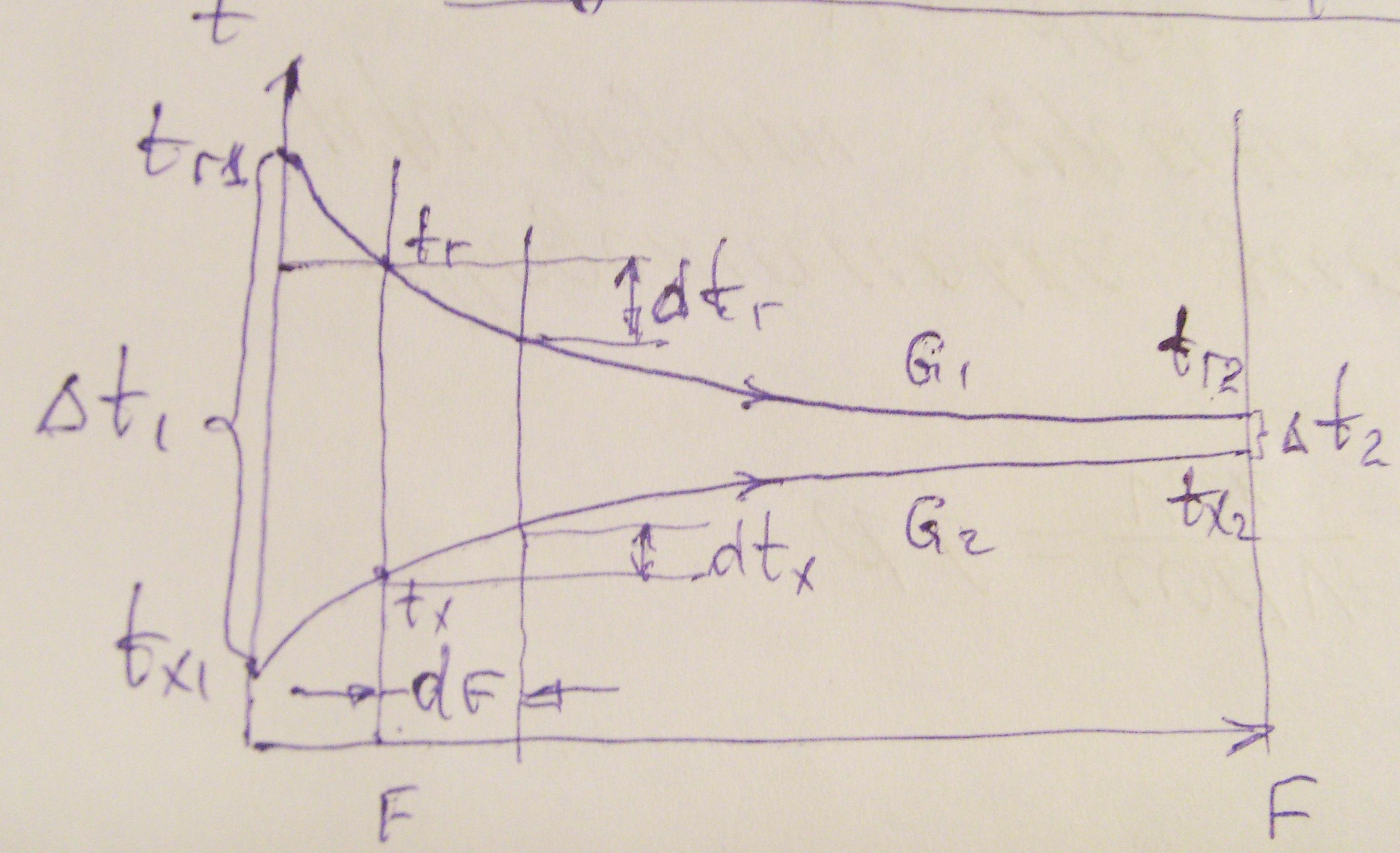
Хай G_г і G_х – витрати гарячої і холодної рідини, кг/с;

С_г і С_х – питома теплоємність гарячої і холодної рідини, Дж/(кгград);

t_г1, t_г2, t_х1, t_х2 – температури гарячої і холодної рідини на вході і виході із апарату, град.

Необхідно визначити t_ср.

Виділимо в теплообмінну елементарну ділянку площею dF і розглянемо тепловий баланс для неї.

Хай dt_г, dt_х – зміна температури гарячої і холодної рідини на цій ділянці;

t = t_г – t_х – рушійна сила теплопередачі на цій ділянці.

Кількість тепла, що віддає гаряча рідина на цій ділянці:

dQ = - G_гС_гdt_г, звідки dt_г = - (1)

Кількість тепла, що одержує холодна рідина:

dQ = G_хС_хdt_х, звідки dt_х = - (2)

Відрахувавши (2) із (1) одержимо:

t

По рівнянню теплопередачі кількість тепла, що передається від гарячої рідини до холодної:

t

Підставимо (4) в (3):

Після інтегрування маємо:

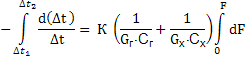
Визначимо і через теплову загрузку апарата і зміну температур гарячої і холодної рідин в ньому.

Кількість тепла, що віддає гаряча рідина через всю поверхню:

Q = G_гС_г(t_г1 - t_г2), звідки (6)

Кількість тепла, яке одержує холодна рідина в апараті:

Q = G_хС_х(t_х2 – t_х1), звідки (7)

Підставляємо (6) і (7) в (5), одержимо:

або

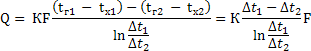
Таким чином:

де t₁ t₂ – рушійна сила теплопередачі на одному і другому кінцях апарату відповідно.

Якщо t₁ / t₂  2, то - середньо арифметична різниця температур.

Середня різниця температур при протитоку

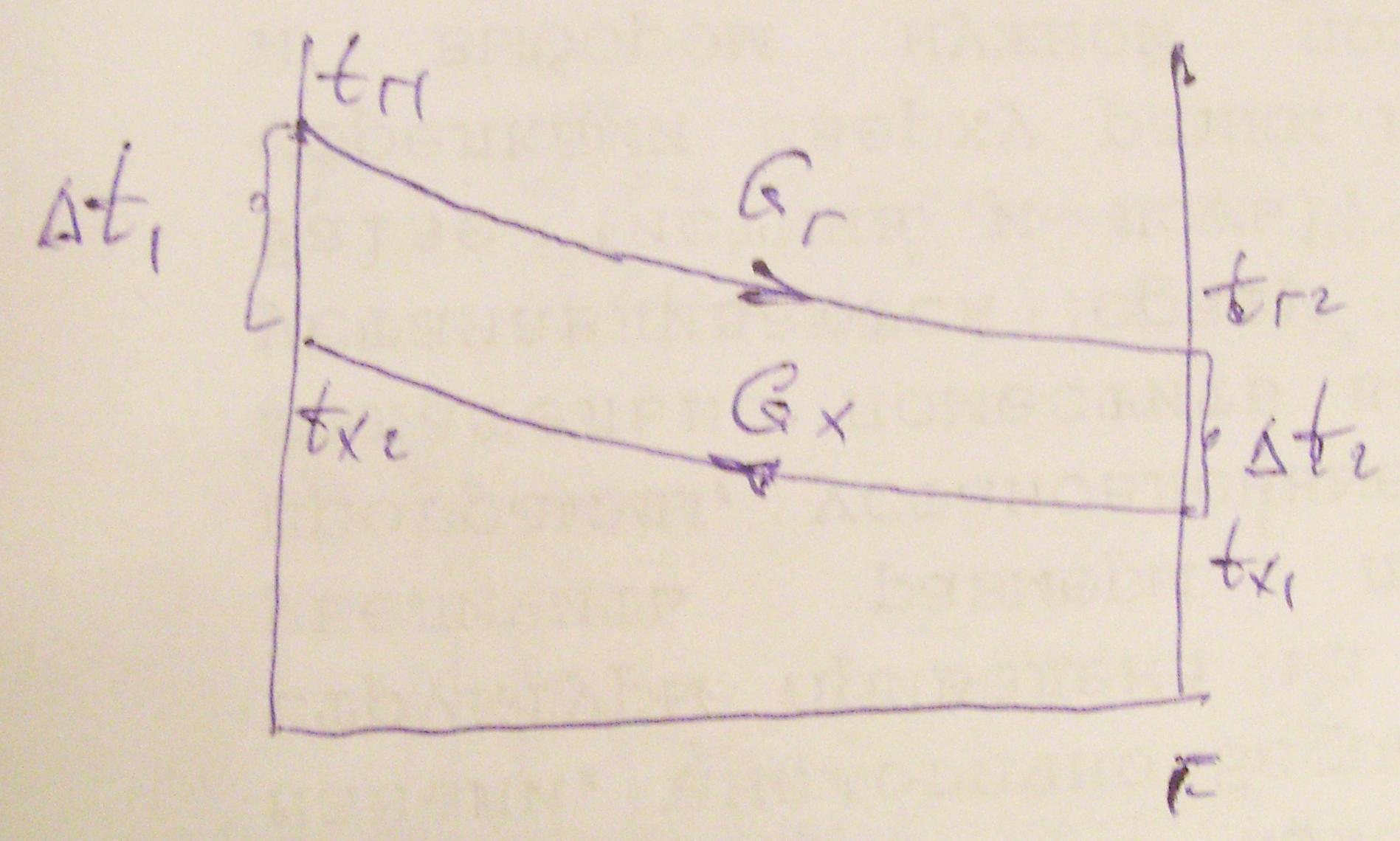
Вирішуючи задачу аналогічним шляхом, одержуємо той же результат:

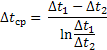
Середня різниця температур при перехресному і змішаному токах рідин

При однакових початкових і кінцевих температурах теплоносіїв:

Величини t_пхт і t_змт визначають в долях t_птт, тобто t_пхт = ₁t_птт і t_змт = ₂t_птт. Значення ₁ і ₂ для різних схем руху теплоносіїв наведені в довідковій літературі.

3.4. Порівняння прямо току і протитоку

Протиточна схема руху теплоносіїв має ряд переваг перед прямоточною, що обумовлює більш широке застосування її в технології. Переваги проти точної схеми заключаються в наступному:

1. Кількість тепла, яке може бути передане від гарячої рідини до холодної при протитоці значно більше, ніж при прямотоці.

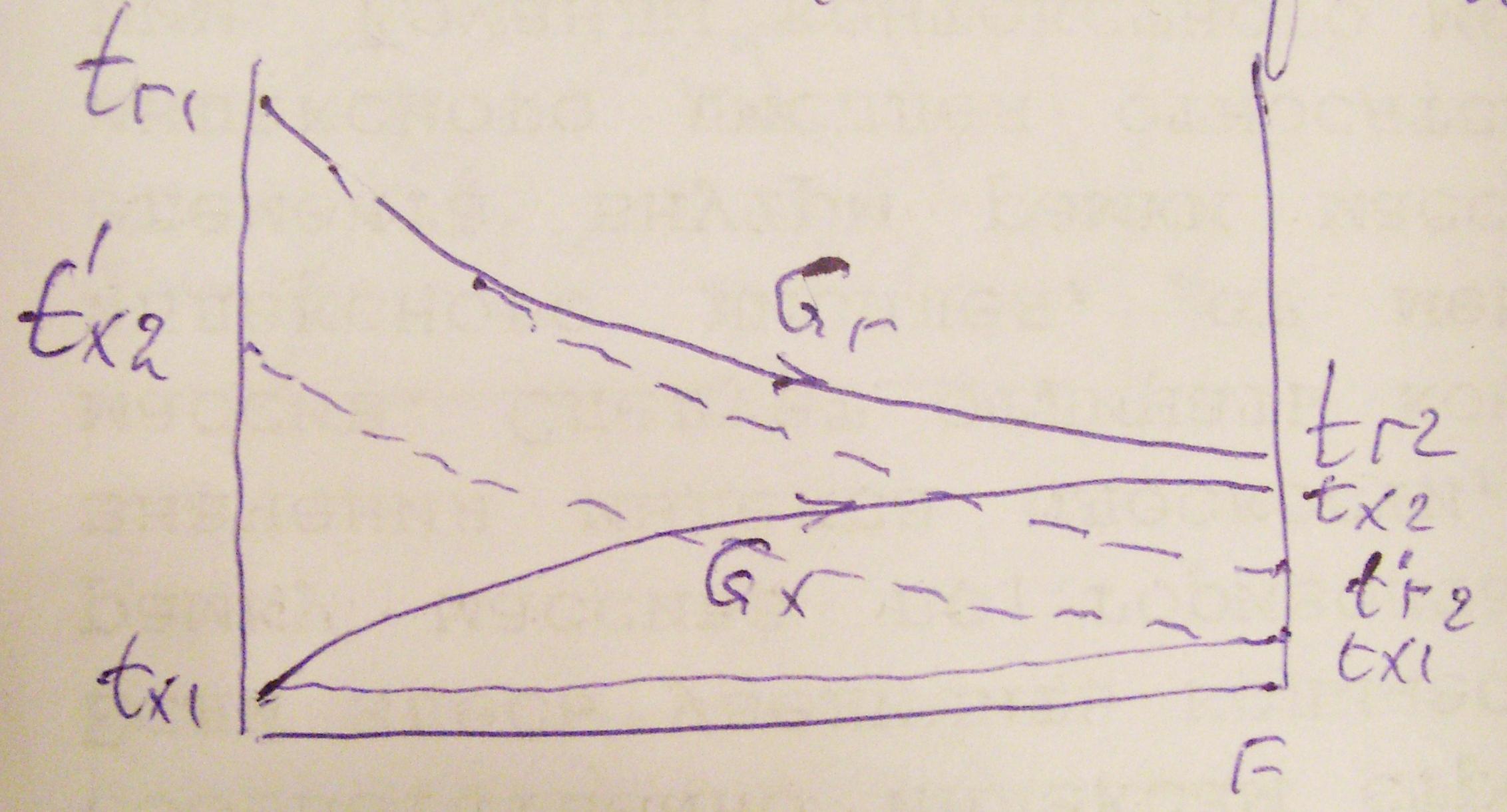
При прямотоці:

Q_пмт = G_гС_г(t_г1 - t_г2) = G_хС_х(t_х2 – t_х1)

При протитоці:

Q_птт = G_гС_г(t_г1 - t_г2^’) = G_хС_х(t_х2^’ – t_х1)

Оскільки (t_г1 - t_г2^’)  (t_г1 - t_г2), то Q_птт  Q_пмт.

2. При заданих початкових і кінцевих температурах теплоносіїв t_ср при протитоці більше, ніж при прямотоці.

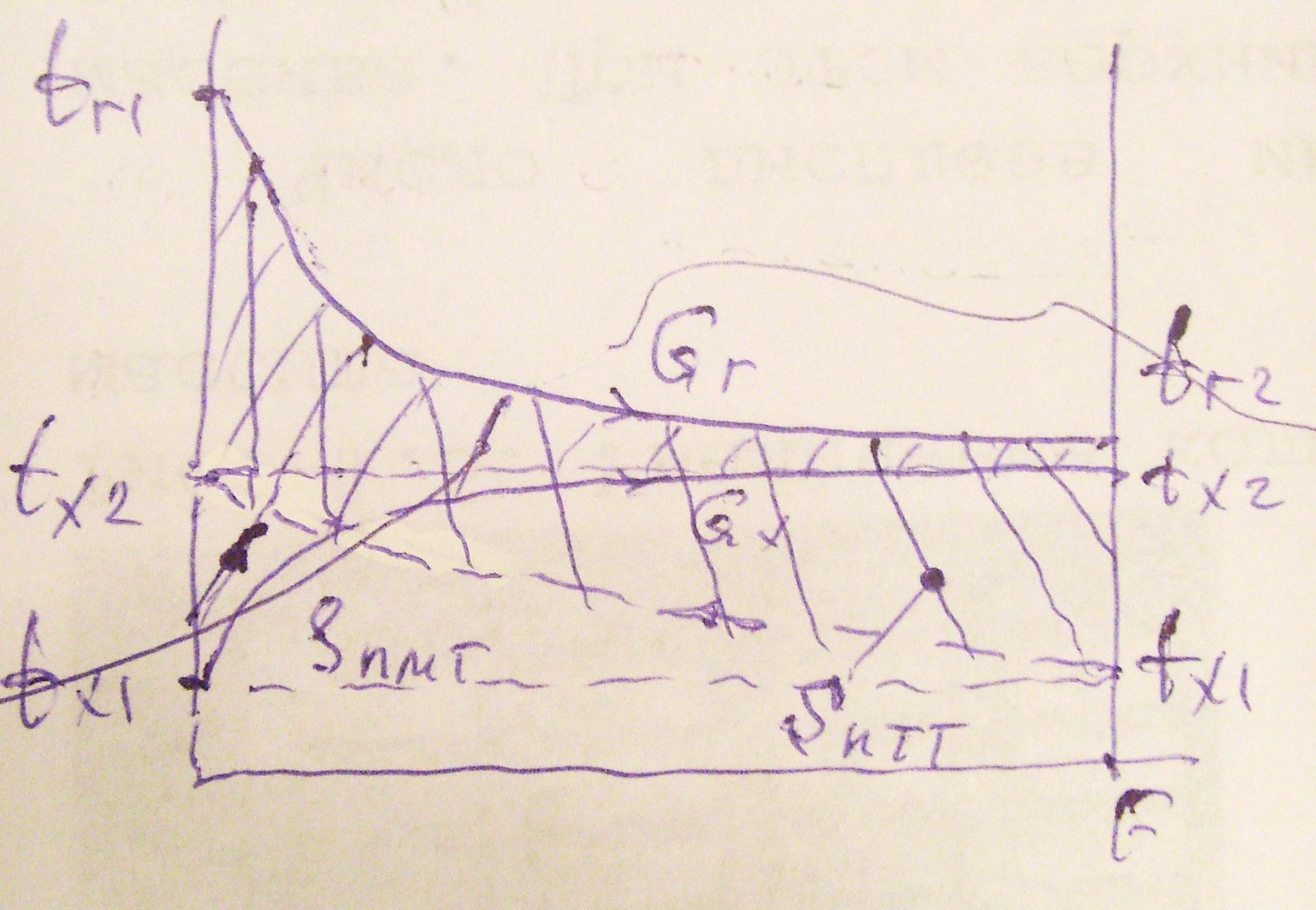
Тому для передачі однакової кількості тепла при протитоці необхідна менша поверхня теплопередачі. Дійсно t_птт  S_птт, а t_пмт  S_пмт. На діаграмі видно, що S_птт S_пмт, тому t_птт  t_пмт, а .

3. Для охолодження заданої кількості гарячої рідини від t_г1 до t_г2 при протитоці потрібно менша витрата холодної рідини.

Оскільки (t^’_х2 - t_х1)  (t_х2 - t_х1), то G_{х птт}  G_{х пмт}.

В окремих випадках, коли температура одного або обох теплоносіїв є постійною по всій поверхні теплопередачі, взаємний напрямокруху теплоносіївне має впливу на t_ср і необхідну поверхню теплопередачі.

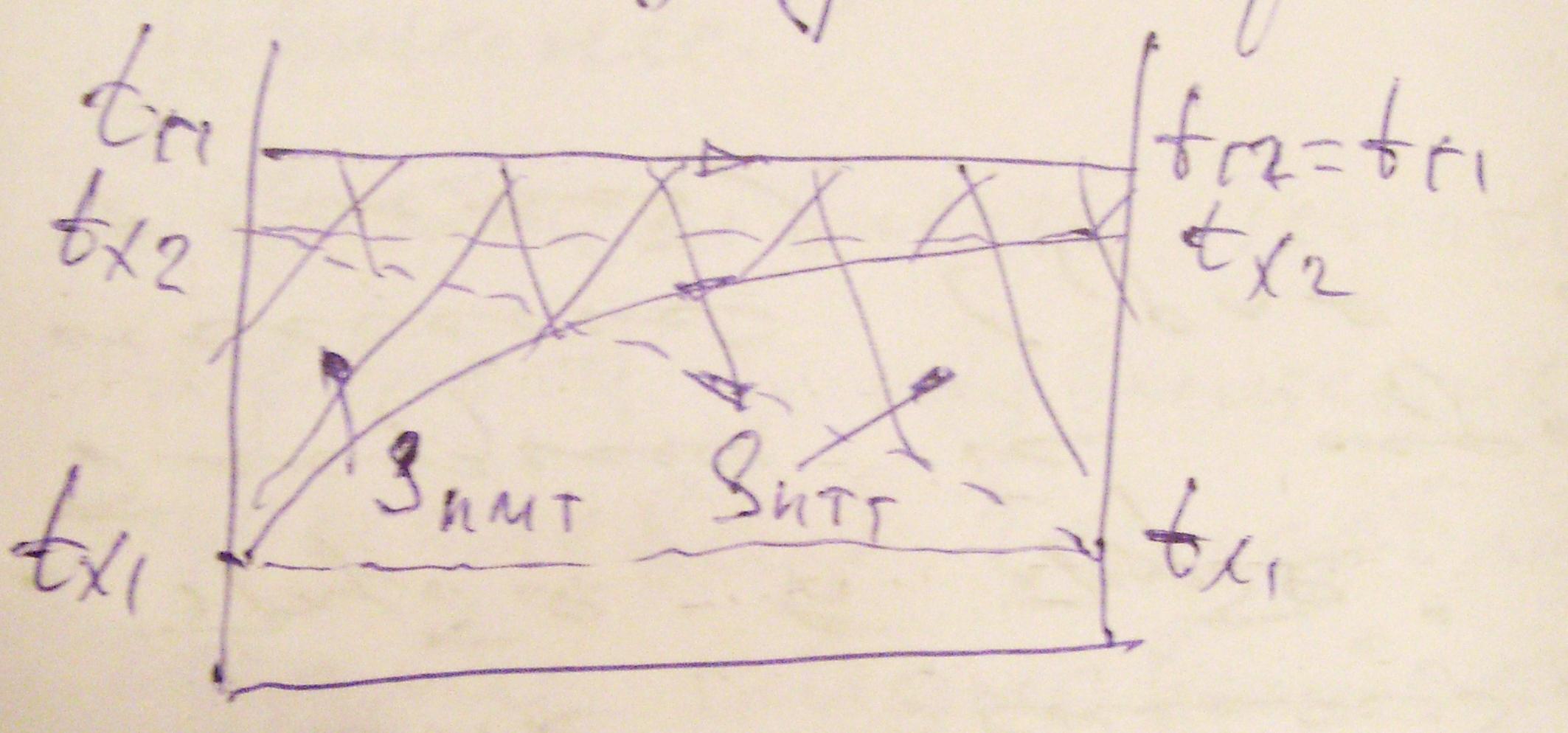
Оскільки S_пмт = S_птт, то t_пмт = t_птт і F_пмт = F_птт.

4. Теплове випромінювання.

Всі тіла здатні випромінювати енергію і поглинати енергію, випромінювану іншими тілами.

Тверді тіла мають безперервний спектр випромінювання, тобто вони здатні випромінювати хвилі будь-якої довжини при будь-якій температурі.

Гази мають смугастий спектр, тобто вони здатні випромінювати хвилі тільки визначеної довжини.

Інтенсивність теплового випромінювання збільшується з підвищенням температури. При t  600 ⁰С променевий теплообмін між твердими тілами і газами стає переважним, тобто він в декілька разів інтенсивніший за конвективний або молекулярний перенос.

Для рідин теплове випромінювання не має практичного значення тому, що його інтенсивність незначна в порівнянні з конвективним теплопереносом.

1. Закони теплового випромінювання

   1. Закон збереження енергії

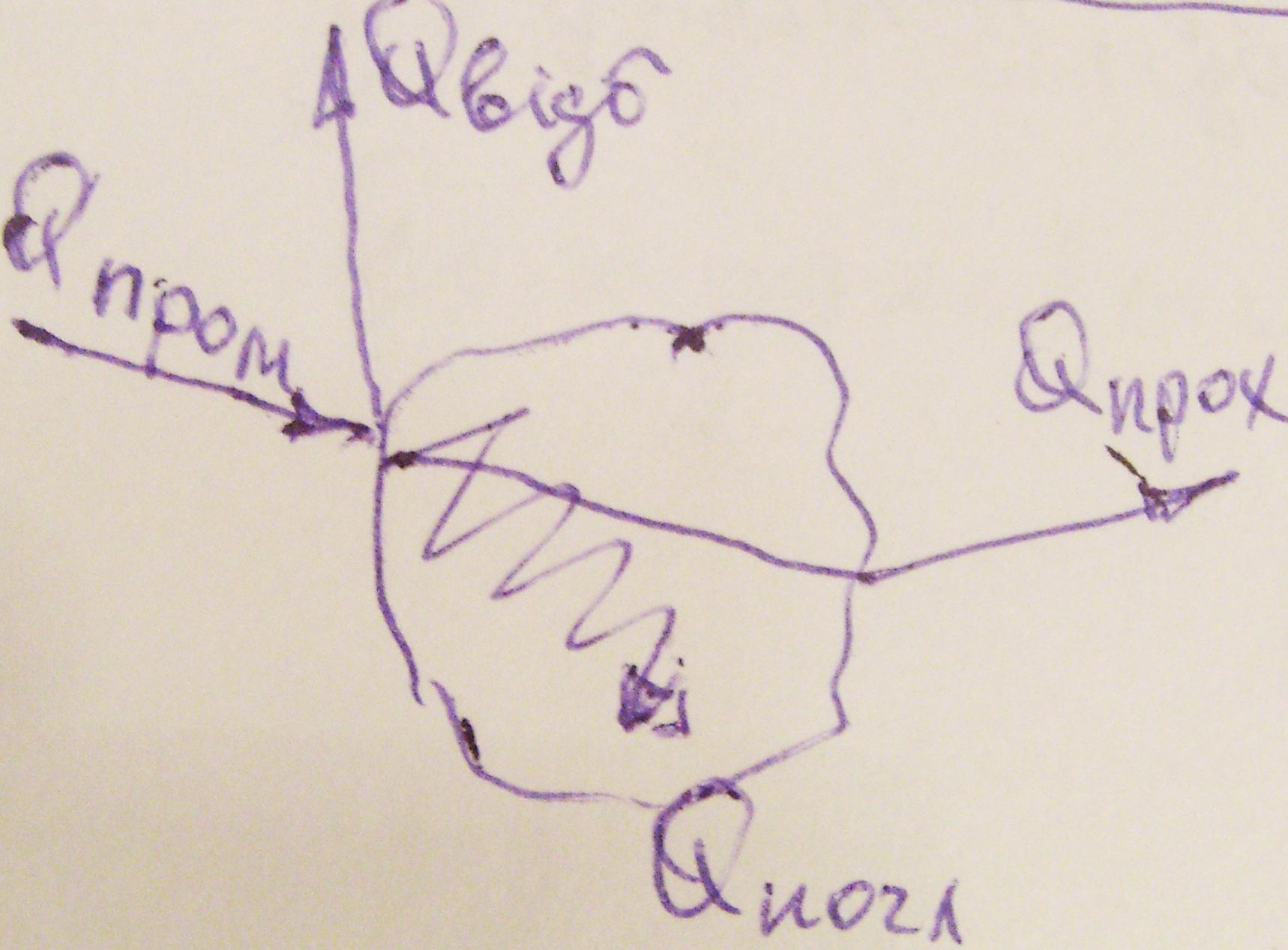
Тепловий потік, що падає на поверхню тіла, рівний сумі відбитого, поглинутого і пройденого крізь тіло потоків.

Рівняння балансу має вигляд:

Q_пром = Q_погл + Q_відб + Q_прох або

В залежності від співвідношення між цими потоками всі тіла ділять на 4 групи:

• абсолютно чорні, які повністю поглинають променевий потік, що падає на їх поверхню 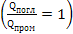. Близькими до цієї групи є тіла, поверхня яких покрита шаром сажі;

• абсолютно білі, які повністю відбивають променевий потік 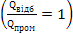. Для полірованої поверхні алюмінію Q_відб / Q_пром 0,97;

• абсолютно прозорі (діатермічні), які повністю пропускають через себе променевий потік, що падає на їх поверхню, тобто 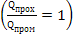. Близькими до цієї групи є скло, двохатомні гази (N₂,O₂, H₂), одноатомні гази (Ne, Не та інші);

• сірі тіла, які частково відбивають, а частково поглинають або пропускають променевий потік, що падає на їх поверхню. Більшість природних тіл відносяться до цієї групи.