19

Часть 1. Математические основы теории искусственного интеллекта

1.1. Общие сведения

Пусть имеется универсальное множество объектов U. Понятие «универсальное множество» означает, что не существует объектов, не принадлежащих множествуU.

Пусть имеется множество объектов B= {x}U. Пусть у каждого объектаxUимеется свойство{0;1} принадлежности к множествуB. МножествоBназываютчетким множеством, т.к. отношение любого объекта универсального множества к нему бинарно (принадлежит/не принадлежит). Свойствоназываютчеткой логической (булевой) переменнойиливысказыванием. Функцию_B(x){0;1}, определяемую на множествеU, называютчеткой логической (булевой) функциейилипредикатом.

Рассмотрим более общий случай. Пусть имеется множество объектов FU, информация о котором нечетка, т.е. состав множества известен недостоверно. Это означает, что для каждого объектаxUможно указать вероятность[0;1] принадлежности его множествуF. ПоэтомуFсчитают множеством парF= {x,_F(x)} и называютнечетким множеством. Функцию принадлежности_F(x)[0;1] называютнечеткой логической функцией, а величину[0;1] -нечеткой логической переменной.

Выражение, содержащее несколько логических переменных, объединенных логическими функциями, называется предложениемилиформулой.

Совокупность правил, используемых для определения истинности или ложности логической формулы, называется исчислением. В частности, ИВ – высказываний, ИП - предикатов.

1.2. Основные операции и функции

Таблица 1 - Основные логические функции

Наименование	Тип	Обозначение
Отрицание, дополнение	Унарный	not,-, ~, не, 
Конъюнкция, пересечение	Бинарный	And, &, и, *, , 
Дизъюнкция, объединение	Бинарный	or, |, или, +, , 
Импликация, включение, доминирование	Бинарный	, =>, , 
Эквивалентность	Бинарный	, 
Разность	Бинарный	-
Дизъюнктивная сумма, исключающее ИЛИ	Бинарный	
Алгебраическое произведение	Бинарный	
Алгебраическая сумма	Бинарный

1.3. Основные понятия

Специфика ИВ по отношению к ИП и нечеткой логике порождает ряд понятий:

Литеройназывают элементарное высказывание (P) или его отрицание (~P).

Дизъюнктомназывают дизъюнкцию конечного числа литер. Пустой дизъюнкт – невыполнимый дизъюнкт. Он обозначается символом "#". Хорновским называют дизъюнкт, содержащий не более одной позитивной литеры.

Конъюнктивная нормальная форма (КНФ)- конъюнкция конечного числа дизъюнктов.

Формула выполнима, если она может быть истинной. Например,pvq, гдеp,v,q- высказывания, - выполнимая формула.

Формула невыполнима, если она не может быть истинной. Например,p(~p) - невыполнимая формула.

Формула общезначима, если она истинна независимо от истинности значений составляющих ее высказываний. Например, ~~p=p- общезначимая формула, т.к. она верна при любомp. Общезначимые формулы называют такжетавтологиями. Формулы, не являющиеся общезначимыми, называют необщезначимыми.

Понятия ИП.

Понятие предиката введено в п. 1.1. Предикаты называются также предикатными именами. Это определение отражает тот факт, что предикат есть имя функции. Более широким понятием ИП является понятие функционального имени.Функциональное имя- это имя функции произвольного (не обязательно булевского) типа.

Литеройв ИП называют предикат или его отрицание.

В частном случае предикат может быть логической формулой, и тогда к нему применимы понятия выполнимости и общезначимости.

Понятия нечеткой логики.

Величина называетсявысотойнечеткого множестваF.Нечеткое множествоFнормально, если. Принечеткое множество называетсясубнормальным. Очевидно, что для четкой логики понятие нормальности не имеет смысла.

Нечеткое множество пусто, если. Непустое субнормальное множество можно нормализовать по формуле:

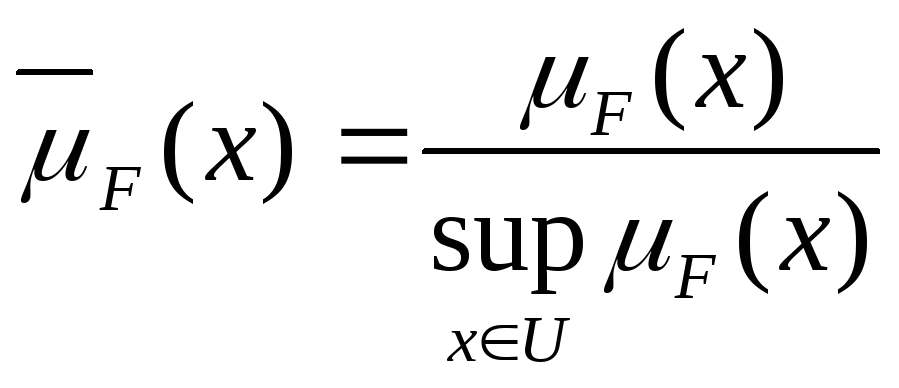
Нечеткое множество унимодально, если_F(x) = 1 только для одного объектаxизU. Объектxв этом случае называютмодой. Понятие унимодальности правомерно также для предикатов: предикат является унимодальным, если он тождественно истинен только для одной комбинации значений своих аргументов.

Точками переходанечеткого множестваFназываются объектыxU:_F(x) = 0.5.