
Физика / Физика / Молекулярная физика (11-18) PDF / Мет. 14
.pdfФедеральное агентство по образованию РФ Ухтинский государственный технический университет
14
Определение динамической вязкости жидкости по методу падающего шарика
Методические указания к лабораторной работе для студентов всех специальностей дневной и заочной формы обучения
Ухта
2007
УДК 53(075) Б 73
ББК 22.3 Я7
Богданов, Н.П. Определение динамической вязкости жи дкости по методу падающего шарика [Текст]: метод. указания/ Н.П. Богданов, И.Н.Андронов. – Ухта: УГТУ, 2007. – 11с.
Методические указания предназначены для выполнения лабораторной р а- боты по физике по теме «Молекулярная физика» для студентов специал ь- ностей 290700, 290300 и направлению 550100.
Содержание методических указаний соответствует рабочей учебной пр о- грамме.
Методические указания рассмотрены и одобрены кафедрой физики от 19.02.07., пр. № 5.
Рецензент: Шамбулина В.Н., доцент кафедры физики Ухтинского государственного технического университета.
Редактор: Северова Н.А., доцент кафедры физики Ухтинского государственного технического университета.
В методических указаниях учтены предложения рецензента и редактора. План 2007 г., позиция 58.
Подписано в печать 30.11. 07г. |
Компьютерный набор. |
Объем 11 с. Тираж 60 экз. |
Заказ №215. |
Ухтинский государственный технический университет, 200 7 169300, г. Ухта, ул. Первомайская, 13.
Отдел оперативной полиграфии УГТУ. 169300, г. Ухта, ул. Октябрьская, 13.
3
ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКОЙ ВЯЗКОСТИ
ЖИДКОСТИ ПО МЕТОДУ ПАДАЮЩЕГО ШАРИКА
Цель и содержание работы
Целью работы является ознакомление с одним из методов опред е- ления динамической вязкости жидкости с п омощью падающего в этой жидкости шарика.
Краткая теория работы
Всякая реальная жидкость обладает вязкостью, т.е. свойством оказывать сопротивление при перемещении одного слоя жидкости относ и- тельно другого.
Согласно молекулярно-кинетической теории строения вещества жидкость представляет совокупность молекул, ра сположенных очень близко друг другу и непрерывно находящихся в беспорядочном колеб а- тельном движении около некоторых средних положений равновесия. При этом молекула многократно сталкивается с соседними молекулами, обмениваясь с ними импульсом и энергией.
При низких температурах (вблизи температуры отвердевания) мол е- кулы под действием приложенной внешней силы могут лишь немного смещаться относительно положения равновесия, испытывая действие у п- руго-вязких сил. Никакого скольжения слоев в этом случае не возникает.
Перемещение одного слоя жидкости относительно др угого может происходить лишь тогда, когда молекулы получают возможность систем а- тически изменять свое положение относительно других молекул. Таким образом, упруго-вязкие силы характеризуют сопротивление перемещению слоев жидкости под действием вне шних сил.
При повышении температуры возрастает среднее ра сстояние между молекулами, увеличивается запас энергии молекул, жидкость становится как бы «пористой» и, при подходящих условиях, молекулы проскакивают между раздвинувшимися соседними молекулами, т.е. скачками перех одят из одних временных положений равновесия в другие, выходя из окруж е- ния своих ближайших соседей - молекул и начинают колебаться относ и- тельно других положений равновесия.
По образному выражению Я.И.Френкеля такое повед ение молекул жидкости называется «оседло-кочевым».
4
Такие скачки происходят беспорядочным образом, однако под де й- ствием разности давлений эти перескоки молекул принимают более направленный характер, молекулы ч аще начинают перемещаться в сторону более низкого давления, и начинается скольжение одного слоя по другому. Так как время между последовательными скачками молекул м ало, то такое прерывное движение воспринимается как непр ерывное скольжение.
Чем реже молекулы изменяют свои положения равновесия, тем м е- нее текуча и более вязка жидкость.
При увеличении температуры вязкость жидкости уменьшается, так как возрастает возможность скачкообра зных переходов молекул.
Силы, действующие между скользящими друг относительно друга слоями жидкости, называются силами внутреннего трения или силами вязкости. Эти силы направлены по касательной к поверхностям слоев.
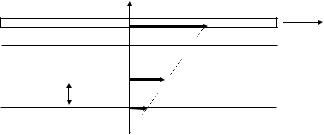
Рассмотрим однородную жидкость, заключенную ме жду плоскими параллельными поверхностями, скользящими друг относительно друга (рис.1)
Под действием внешней силы F поверхность I движется равномерно со скоростью 0 относительно неподвижной поверхности II.
Частицы жидкости, прилегающие непосредственно к поверхности I, прилипают к ней, образуя связанную с поверхностью тонкую пленку. Эта пленка полностью принимает участие в движении поверхности I со скоростью 0 , слой жидкости, прилегающий к этой пленке, отстает от после д-
ней; точно так же каждый следующий слой жидкости, более отдаленный от поверхности I, отстает от слоев, более близких к поверхности I. Слои при этом скользят друг относительно друга, не перемешиваясь. Такое т е- чение жидкости называется ламинарным (слоистым).
У F
I
|
|
|
0 |
|
|
|
|
+d |
|
|
|
|
|
|
|
|
dy |
|
|
II |
|
|
|
|
|
|
|
|
|
|
|
Рис.1. |
|
|
|
|
|
|
Ламинарное течение стационарно - скорости частиц жидкости зависят от расстояния до стенок и это распредел ение скоростей не изменяется со временем.
Пусть два соседних слоя жидкости, расстояние между которыми dy , движутся со скоростью и dv . Отношение d / dy будет характе-

5
ризовать изменение скорости в направление оси Y . Это отношение называется градиентом скорости.
Ньютоном было установлено, что сила внутреннего трения FТР про-
порциональна поверхности S соприкасающихся слоев жидкости и град и- енту скорости по направлению, перпендикулярному к направлению дв и- жения потока:
Fm р |
d |
S . |
(1) |
|
|||
|
dy |
|
|
Коэффициент пропорциональности в формуле (1), характеризую-
щий свойства данной жидкости, называется динамической вязкостью. Из формулы (1) имеем:
|
Fm р |
. |
(2) |
||
|
|||||
|
S |
d |
|||
|
|
|
|
|
|
dy
Динамическая вязкость на основании формулы (2) численно равна
силе внутреннего трения, действующей на единицу поверхности соприкасающихся слоев жидкости, при градиенте скорости, равном ед и-
нице. В системе СИ динамическая вязкость измеряется в Н с/м2.
Динамическая вязкость равна 1Н с/м2, если при градиенте скорости 1с-1 действует сила внутреннего трения в 1 Н.
Размерность в системе СИ [ ] = Н с/м2 = кг/м с.
Размерность в системе СГС 1пз = дин с/см2 = г/см с.
Единицей динамической вязкости в системе СГС явл яется пуаз (пз). В зависимости от рода жидкости и температуры динамическая вяз-
кость |
меняется в широких границах: от 10 |
-5 н c |
для газов, до 10 |
9 |
|
|
м2 |
|
|||
|
|
|
|
|
|
н 2c для битума при 150С.
м
Величина коэффициента динамической вязкости имеет большое значение при определении качества смазочных материалов, при ра с- чете движения нефти и нефтепродуктов по трубопроводам, расчете подачи топлива в двигателях внутреннего сгорания и в р яде других случаев.

6 |
|
В данной лабораторной работе динамическая вязкость |
определя- |
ется из закона Стокса: |
|
FТР 6 r . |
(3) |
Эта формула, полученная путем сложных расчетов из формулы (1), определяет величину силы внутреннего трения FТР , действующую на ша-
рик радиуса r , движущийся с небольшой скоростью в вязкой среде. Формула (3) справедлива при следующих условиях:
1) малые скорости движения такие, при которых чи сло Рейнольдса - порядка единицы:
r ж 1 ,
2) среда, в которой движется шарик, практически безгранична, это значит, что стенки сосуда находятся далеко от шарика.
Если учесть, что сосуд, в котором движется шарик, имеет конечные размеры, то для случая, когда шарик падает вдоль оси цилиндрического сосуда радиуса R , сила внутреннего трения FТР будет равна:
FТР |
= 6 r (1 2,4 |
r |
) . |
(4) |
|
||||
|
|
R |
|
|
На шарик радиуса r и плотности ш , движущийся в вязкой среде, будут действовать следующие силы (рис.2.):
1) сила тяжести
P mg ш0 g |
4 |
r 3 ш g |
, |
(5) |
|
3 |
|
|
|
2) сила внутреннего трения |
|
|
|
|
FТР 6 r k , |
|
(6) |
||
где через k обозначен коэффициент при скорости в формуле Стокса (3);
3) выталкивающая сила, определяемая по закону Архимеда,

|
|
7 |
|
|
FА = |
4 |
πr 3 ρж g |
, |
(7) |
|
3 |
|
|
|
где ж - плотность жидкости, в которой движется шарик.
Вес и выталкивающая сила при движении шарика остаются пост о- янными. Сила же внутреннего трения растет по ме ре увеличения скорости. В определенный момент вес тела уравновесится силами, направленными вертикально вверх, и движение шарика станет равномерным. Следов а- тельно
P FA FТР
или
4 |
r 3 ш g |
4 |
r 3 с g 6 r V |
, |
||
3 |
|
|
3 |
|
|
|
откуда |
|
|
|
|
|
|
|
|
2r 2 |
( ш ж )g |
. |
(8) |
|
|
|
|
9 |
|||
|
|
|
|
|
|
|
|
F |
|
FA |
|
|
|
P |
|
Рис.2. |
Выразив радиус шарика r через диаметр d, а скорость падения V через
путь и время t, получим окончательную формулу для определения коэффициента вязкости:
|
d |
2 ( ш ж )gt |
. |
(9) |
|
18 |
|||
|
|
|
|

8
Приборы и принадлежности, необходимые для выполнения лабораторной работы
1.Стеклянный сосуд с жидкостью, вязкость которой необходимо опред е- лить.
2.Стальные шарики диаметром 0,8 - 1,5 мм.
3.Микрометр для измерения диаметров шариков.
4.Масштабная линейка для измерения пути, пройденного шариком ме ж- ду двумя метками на сосуде.
5.Секундомер для измерения времени падения шарика.
Выполнение работы
1.Верхнюю метку (металлическое колечко) расположить на расстоянии 4-5 см от поверхности жидкости, а нижнюю - на расстоянии 4-5 см от дна сосуда и измерить расстояние между ними.
2.Измерить с помощью микрометра диаметр первого шарика в нескол ь- ких местах и записать в таблицу среднее значение dСР диаметра.
3.Опустить шарик в жидкость, как можно ближе к оси с осуда. В момент прохождения шариком верхней метки включить секундомер и выкл ю- чить в момент прохождения нижней. Записать в таблицу время пад е- ния шарика.
4.Повторить измерения диаметра и времени падения еще для четырех шариков.
5.Выписать из справочных таблиц на стене лаборатори и плотности шарика и жидкости.
6.По формуле (9), представив ее в виде
Аd2t |
, где |
А |
ш ж |
g |
|
18 |
|||||
|
|
|
|
вычислить значение коэффициента вязкости по результ атам каждого опыта и найти среднее значение.
7. По формуле:
|
|
d 2 |
|
|
щ с |
2 |
|
g 2 |
|
t 2 |
|
2 |
||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
щ с |
|
|
|
|
|
|||||||
|
d |
|
|
|
|
|
g |
|
t |
|
|
|
|
|||
найти относительную и абсолютную погрешности измерения коэффициента динамической вязкости .
9
Таблица измерений и вычислений
№№ |
ш |
ж |
|
А |
d ср |
t |
|
|
|
cр |
пп |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы
1.Почему скорость течения вязкой жидкости различна в разных сечениях потока?
2.Что такое градиент скорости?
3.Объясните причины вязкости жидкости.
4.Дайте определение единицы динамической вязкости в системе СИ.
5.Как будут отличаться установившиеся скорости движения для шар и- ков разных диаметров?
6.Как зависит вязкость от температуры?
7.Почему верхнюю метку на цилиндре следует располагать на некот о- ром расстоянии от поверхности жидкости?
8.Какие силы действуют на шарик, падающий в жидкости?
Индивидуальные задания
1.Самолет летит со скоростью 360 км/ч. Считая, что слой воздуха у крыла увлекаемый вследствие вязкости, равен 4 см , найти: а) градиент скорости в слое увлекаемом вследствие вязкости, б) касательную силу,
действующую на каждый метр поверхности крыла. Коэффиц иент вязкости воздуха равен 2. 10-5 Н с./м2 .
2.Смесь свинцовых дробинок диаметром 3 мм и 1 мм опустили в бак с глицерином глубиной H =1м. На сколько позже упадут на дно дробин-
ки меньшего диаметра по сравнению с дробинками большего диаме т- ра? Вязкость глицерина =1.47 Н с./м2.(Сила трения, действующая со стороны жидкости на дробинки, действует по закону Стокса).
3.Высокий сосуд наполнен маслом, коэффициент вязк ости которой 0.5 Нс./м2. По оси цилиндра опускают маленький свинцовый шарик. Слои жидкости движутся со скоростью, которая меняется с расстоянием r
от трубки по закону u u0 (1 r 2 / R 2 ) , (u =0.25 м/с, R =5 см). Найти:
10
а) градиент скорости вблизи стенки трубки ; б) силу трения, которую испытывает единица длины поверхности трубки со стороны жидк о- сти.
4. Какой наибольшей скорости может достичь дождевая капля диаме т- ром d =0.3 мм, если динамическая вязкость воздуха равна 1,2 .10-4 г/см.с. Плотность воздуха 1,29 кг/м3. Плотность воды 103 кг/м 3 . (Сила трения, действующая на каплю, рассчитывается по закону Ст окса).
5.Шарик всплывает с постоянной скоростью в жидкости, плотность к о- торой в четыре раза больше плотности м атериала шарика. Во сколько
раз сила трения FТР , действующая на шарик, больше веса P этого шарика? (Сила трения на шарик FТР со стороны жидкости действует по закону Стокса).
6.В широком сосуде, наполненном глицерином (плотность =1.2 г/см3),
падает с установившейся скоростью 5 см/ с стеклянный шарик ( =2.7 г/ см3) диаметром 1мм. Определить динамическую вязкость глице-
рина.
Ответ: 1,6 Па.c
7. Тонкая плоскопараллельная пластинка площадью S находится в потоке жидкости, текущей вдоль ее поверхности. Определить вя зкость жидкости, если на пластинку действует сила F , а градиент скорости в месте её нахождения равен K .Ответ .
8.В высокий цилиндрический сосуд, наполненный глицерином, брос ают алюминиевый шарик диаметром d =6мм. Определить, при какой скорости падение шарика станет равномерным. Ламинарным или турб у- лентным будет при этом движение жидкости? Критическое число Ре й- нольдса Reкр=2300. Ответ:V =0,0198м/с, движение ламинарное
9. Стальной шарик радиусом r =2.10-3 м падает в жидкости со скоростью V =0,2м/с. Определить вязкость жидкости, если ее плотность равна 1,2.10 3кг/м3. Ответ: 0,290 Па.с
10. Определить время подъема движущихся с постоянной скоростью п у- зырьков воздуха со дна водоема глубиной 1м, если диаметры пузыр ь- ков соответственно равны 2 и 1 мм. Расширением пузырьков прене б- речь. Ответ: 0.505с,2.02 с
