Основы теории теплообмена [1, с.57-68]

Теория теплообмена – это наука о процессах переноса теплоты. Теплообмен представляет собой сложный процесс, который можно расчленить на ряд простых процессов. Различают три элементарных принципиально отличных один от другого процесса теплообмена – теплопроводность, конвекция и тепловое излучение.

Теплопроводность – происходит при непосредственном соприкосновении (соударении) частиц вещества (молекул, атомов, свободных электронов), сопровождающемся обменом энергии. Теплопроводность в газах и жидкостях незначительна. Значительно интенсивнее протекают процессы теплопроводности в твёрдых телах. Тела с малой теплопроводностью называют теплоизоляционными.

Конвекция – происходит лишь в жидкостях и газах и представляет собой перенос теплоты в результате перемещения и перемешивания частиц жидкости или газа. Конвекция всегда сопровождается теплопроводностью.

Если перемещение частиц жидкости или газа обуславливается разностью их плотностей (из-за разности температур), то такое перемещение называют естественной конвекцией.

Если жидкость или газ перемещаются с помощью насоса, вентилятора, эжектора и других устройств, то такое перемещение называют вынужденной конвекцией. Теплообмен происходит в этом случае значительно интенсивнее, чем при естественной конвекции.

Тепловое излучение состоит в переносе теплоты от одного тела к другому электромагнитными волнами, возникающих в результате сложных молекулярных и атомных возмущений. Электромагнитные волны распространяются от поверхности тела во все стороны. Встречая на своём пути другие тела, лучистая энергия может ими частично поглощаться, превращаясь снова в теплоту (повышая их температуру).

Основные понятия и определения [1, с.54-57]

1. Перенос теплоты от одного тела к другому, а также между частицами данного тела происходит только при наличии разности температур и направлен всегда в сторону более низкой температуры.

2. Количество теплоты, переносимой в единицу времени, называется тепловым потоком Q, Вт. Отношение Q к единице площади F, м², называется поверхностной плотностью теплового потока q, Вт/м²:

q=Q/F. (1.2)

3. Температурное состояние тела или системы тел можно охарактеризовать с помощью температурного поля, под которым понимается совокупность мгновенных значений температур во всех точках изучаемого пространства. Температура различных точек тела есть функция координат x, y, z и времени :

t=f(x,y,z,) (1.3)

Температурное поле, изменяющееся с течением времени, называется нестационарным.

Если температура в любой точке тела с течением времени не изменяется, то температурное поле называется стационарным (установившемся), и описывается выражением:

t=f(x,y,z). (1.4)

4. Температурное поле в рассматриваемом теле или системе тел удобно характеризовать с помощью изотермических поверхностей, под которыми понимается геометрическое место точек с одинаковой температурой. Такие поверхности могут быть замкнутыми или выходить на границы тела, но между собой никогда не пересекаются.

Если изотермические поверхности пересечь плоскостью, то на плоскости сечения получим изотермические линии, называемые изотермами.

Изменение температуры в теле наблюдается лишь в направлениях, пересекающих изотермические поверхности (например, направление х, см. рис. 1.1). При этом наиболее резкое изменение температуры получается в направлении нормали n к изотермической поверхности. Производная температуры по нормали к изотермической поверхности называется температурным градиентом:

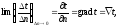[град/м]. (1.5)

Если тепловой поток отнесён к единице изотермической поверхности, то величина q является вектором, направление которого совпадает с направлением распространения тепла в данной точке и противоположно направлению вектора температурного градиента.

Закон Фурье [1, с.57-61]

Изучая процессы распространения тепла в твёрдых телах, Фурье экспериментально установил, что количество переданного тепла пропорционально падению температуры, времени и площади сечения, перпендикулярного направлению распространению тепла.

Если количество переданного тепла отнести к единице сечения и единице времени, то можно записать:

(1.6)

Уравнение (1.6) является математическим выражением основного закона теплопроводности – закона Фурье. Этот закон лежит в основе всех теоретических и экспериментальных исследований процессов теплопроводности. Знак минус указывает, что вектор теплового потока направлен в сторону, противоположную температурному градиенту.

Коэффициент теплопроводности [1, с.57-58]

Множитель пропорциональности  в уравнении (1.6) является коэффициентом теплопроводности. Он характеризует физические свойства тела и способность его проводить тепло:

(1.7)

Величина  представляет собой количество тепла, которое проходит в единицу времени через единицу площади изотермической поверхности при температурном градиенте равном единице.

Для различных веществ коэффициент теплопроводности различный и зависит от природы вещества, его структуры, влажности, наличия примесей, температуры и других факторов. В практических расчётах коэффициент теплопроводности строительных материалов надлежит принимать п СНиП II-3-79** «Строительная теплотехника».

Для примера:

• для газов - =0,0050,5 [Вт/мС]

• для жидкостей - =0,080,7 [Вт/мС]

• строительные материалы и теплоизоляторы - =0,023,0 [Вт/мС]

• для металлов - =20400 [Вт/мС]

Теплопроводность плоской стенки [1, с.57-61]

Рассмотрим однослойную плоскую стенку толщиной , с коэффициентом теплопроводности . На наружных поверхностях поддерживаются постоянные температуры t₁ и t₂, причём t₁>t₂. Теплота распространяется только вдоль оси x. При этих условиях температурное поле в стенке будет одномерным, и изотермическими поверхностями будут плоскости, параллельные поверхностям стенки.

Выделим внутри стенки слой dx, ограниченный двумя изотермическими поверхностями.

На основании закона Фурье можно записать:

или (1.8)

Проинтегрировав данное уравнение, получим:

(1.9)

Из последнего выражения следует, что температура изменяется по толщине стенки по линейному закону. Константа С определяется из условий на границах стенки. В результате получим:

или , Вт/м. (1.10)

Обозначив t=t₁-t₂, выражение (1.10) можно переписать в виде:

, где , м²С/Вт.

Величина R называется термическим сопротивлением стенки. Соответственно, тепловой поток Q через стенку площадью F можно определить по формуле:

, Вт.

Теплопроводность плоской многослойной стенки [1, с.60-61]

Рассмотрим плоскую многослойную стенку, состоящую из n слоёв, плотно прилегающих один к другому (рис. 1.3). Каждый слой имеет заданную толщину _i и коэффициент теплопроводности _i. Многослойными являются, например, стены и перекрытия крупнопанельных и кирпичных зданий.

При стационарном тепловом режиме тепловые потоки, проходящие через каждый из слоёв стенки, одинаковы. Поэтому, пользуясь формулой (1.10) для каждого слоя, можно записать:

(1.11)

Откуда:

(1.12)

Просуммировав правые и левые части этих равенств и выполнив преобразования, получим:

(1.13)

откуда находим q, Вт/м²:

(1.14)

где: t – температурный перепад, т.е. разность температур наружных поверхностей стенки;

R=R₁+R₂+...+R_n – общее термическое сопротивление многослойной стенки, равное сумме термических сопротивлений отдельных слоёв.

Температурное поле многослойной стенки представляет собой ломаную линию (см. рис. 1.3).