- •Системный анализ в менеджменте
- •Оглавление
- •Часть 5. Теория игр и принятие решений 44
- •Ключевые слова
- •Основные понятия
- •Проблемы согласования целей
- •Часть 1. Принятие решения в условиях определенности
- •1.1 Постановка задачи
- •1.2 Описание алгоритма решения задачи
- •1.3 Пример решения задачи
- •Часть 2. Принятие решения в условиях неопределенности.
- •2.1 Постановка задачи
- •2.2 Описание алгоритма решения задачи
- •2.3 Пример решения задачи
- •Часть 3. Принятие решения в условиях риска
- •3.1 Постановка задачи
- •3.2 Описание алгоритма решения задачи
- •3.3 Пример решения задачи
- •Часть 4. Марковская задача принятия решений
- •4.1 Постановка задачи
- •4.2 Описание алгоритма решения задачи
- •Модель динамического программирования с конечным числом этапов
- •Модель динамического программирования с бесконечным числом этапов
- •Метод полного перебора
- •Метод итерации по стратегиям без дисконтирования
- •4.3 Пример решения задачи для конечного числа этапов
- •4.4 Пример решения задачи с бесконечным числом этапов методом полного перебора
- •4.5 Пример решения задачи с бесконечным числом этапов методом итерации по стратегиям без дисконтирования
- •Часть 5. Теория игр и принятие решений
- •5.1 Постановка задачи
- •5.2 Игра в чистых стратегиях
- •5.3 Игра в смешанных стратегиях
- •5.3.1 Игра в смешанных стратегиях 2х2
- •5.3.2 Игра в смешанных стратегиях 2xn и mx2
- •5.3.3 Решение матричных игр методами линейного программирования
- •5.3.3.1 Решение задачи лп симплекс-методом
- •Заключение
- •Литература
- •Задание на контрольную работу
1.3 Пример решения задачи
Формулировка задачи:
Предприятию необходимо взять в аренду складские помещения для хранения своей продукции. Склад может быть расположен в одном из трех городов: D, B или C.
Руководству предприятия, в составе: Петров П.Е., Иванов И.В. и Некрасова Н.Е., необходимо решить: в каком городе рациональнее расположить склад. Для анализа альтернатив руководство выделило три критерия, оказывающих наибольшее влияние на доходность предприятия: спрос на продукцию (С), наличие конкурентов (К) и стоимость аренды складских помещений (Ар) в каждом из городов.
Основываясь на выдвинутых критериях, руководство должно отдать предпочтение определенному городу.
В каком городе выгоднее, разместить склад, при условии, что мнения экспертов равнозначны?
Решение:
Матрицы парных сравнений критериев:
Петров П.Е.
Иванов И.В.
Некрасов Н.Е.
С
К
Ар
С
К
Ар
С
К
Ар
D=
С
1
5
4
D=
С
1
4
3
D=
С
1
2
5
К
0,2
1
0,5
К
0,25
1
1
К
0,5
1
4
Ар
0,25
2
1
Ар
0,333
1
1
Ар
0,2
0,25
1
Для определения относительных весов критериев «С», «К» и «Ар» нормализуем полученные матрицы сравнения и найдем средние значения элементов соответствующих строк нормализованной матрицы.
|
Петров П.Е. | |||||
|
|
|
С |
К |
Ар |
wi |
|
ND= |
С |
|
|
|
0,681 |
|
К |
|
|
|
0,118 | |
|
Ар |
|
|
|
0,201 | |
Аналогично получаем весовые коэффициенты критериев для других экспертов:
|
Иванов И.В. |
|
Некрасов Н.Е. |
| ||||||||
|
|
|
С |
К |
Ар |
wi |
|
|
С |
К |
Ар |
wi |
|
ND= |
С |
0,632 |
0,667 |
0,6 |
0,633 |
ND= |
С |
0,588 |
0,615 |
0,5 |
0,568 |
|
К |
0,158 |
0,167 |
0,2 |
0,175 |
К |
0,294 |
0,308 |
0,4 |
0,334 | ||
|
Ар |
0,211 |
0,167 |
0,2 |
0,192 |
Ар |
0,118 |
0,077 |
0,1 |
0,098 | ||
Проверим: является ли уровень несогласованности полученных матриц парных сравнений приемлемым.
|
Петров П.Е. | |||||||
|
|
1 |
5 |
4 |
|
0,681 |
= |
2,076 |
|
0,2 |
1 |
0,5 |
0,118 |
0,355 | |||
|
0,25 |
2 |
1 |
0,201 |
0,607 | |||
Отсюда получаем:
nmax = 2,076 + 0,355 + 0,607 = 3,038
Следовательно, для n=3 имеем:
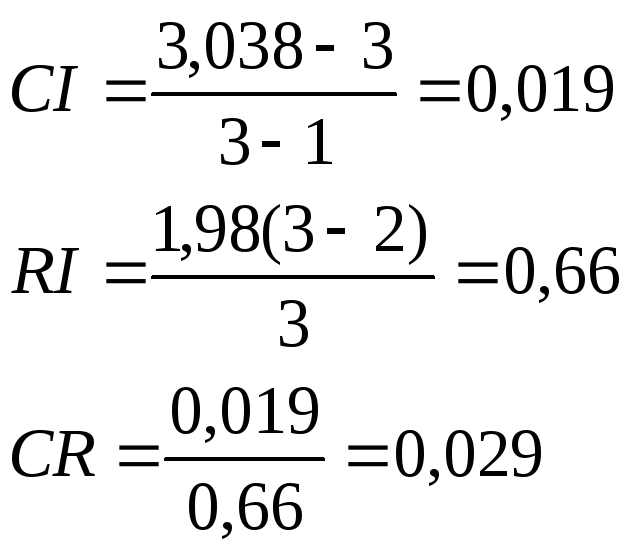
Так как CR<0,1, уровень несогласованности матрицы D является приемлемым.
Аналогично находим:
|
Иванов И.В. | |||||||
|
|
1 |
4 |
3 |
|
0,633 |
= |
1,909 |
|
0,25 |
1 |
1 |
0,175 |
0,525 | |||
|
0,333 |
1 |
1 |
0,192 |
0,578 | |||
Отсюда получаем: nmax = 3,013
Следовательно, для n=3 имеем:
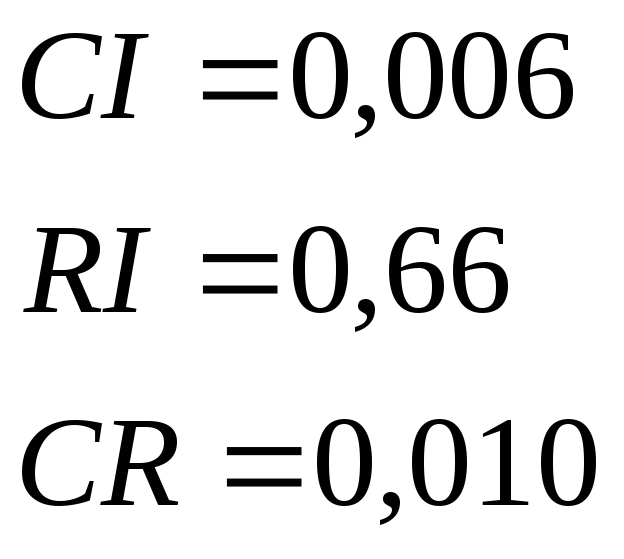
Так как CR<0,1, уровень несогласованности матрицы D является приемлемым.
|
Некрасов Н.Е. | |||||||
|
|
1 |
2 |
5 |
|
0,568 |
= |
1,727 |
|
0,5 |
1 |
4 |
0,334 |
1,011 | |||
|
0,2 |
0,25 |
1 |
0,098 |
0,295 | |||
Отсюда получаем:
nmax = 3,033.
Следовательно, для n=3 имеем:
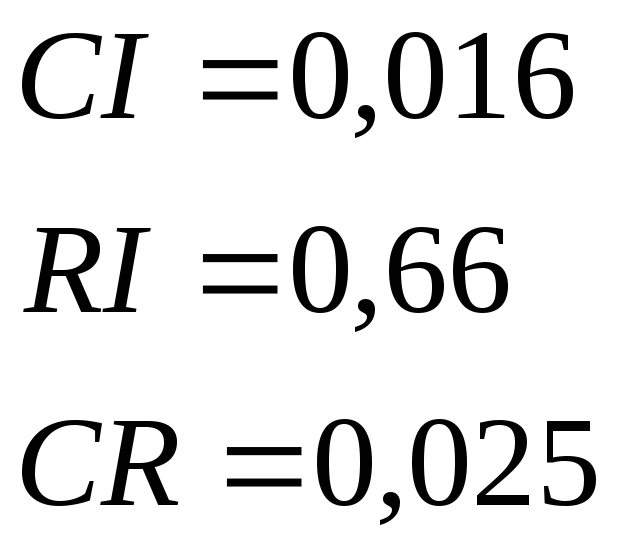
Так как CR<0,1, уровень несогласованности матрицы D является приемлемым.
В результате мы имеем весовые коэффициенты критериев для каждого эксперта, представленные в Таблица 1.
Таблица 1
|
|
Петров П.Е. |
Иванов И.В. |
Некрасов Н.А. |
|
С |
0,681 |
0,633 |
0,568 |
|
К |
0,118 |
0,175 |
0,334 |
|
Ар |
0,201 |
0,192 |
0,098 |
Произведем действия, аналогичные пп.1-3, для получения весов альтернативных решений (D, B и С).
Матрицы парных сравнений альтернатив в соответствии с каждым критерием.
|
Петров П.Е. | ||||||||||||||||
|
DС= |
|
D |
В |
С |
|
DК= |
|
D |
В |
С |
|
DАр= |
|
D |
В |
С |
|
D |
1 |
1 |
2 |
D |
1 |
2 |
3 |
D |
1 |
2 |
0,5 | |||||
|
В |
1 |
1 |
3 |
В |
0,5 |
1 |
2 |
В |
0,5 |
1 |
0,25 | |||||
|
С |
0,5 |
0,333 |
1 |
С |
0,333 |
0,5 |
1 |
С |
2 |
4 |
1 | |||||
|
Иванов И.В. | ||||||||||||||||
|
DС= |
|
D |
В |
С |
|
DК= |
|
D |
В |
С |
|
DАр= |
|
D |
В |
С |
|
D |
1 |
4 |
3 |
D |
1 |
3 |
4 |
D |
1 |
3 |
4 | |||||
|
В |
0,25 |
1 |
0,5 |
В |
0,333 |
1 |
2 |
В |
0,333 |
1 |
2 | |||||
|
С |
0,333 |
2 |
1 |
С |
0,25 |
0,5 |
1 |
С |
0,25 |
0,5 |
1 | |||||
|
Некрасов Н.Е. | ||||||||||||||||
|
DС= |
|
D |
В |
С |
|
DК= |
|
D |
В |
С |
|
DАр= |
|
D |
В |
С |
|
D |
1 |
2 |
5 |
D |
1 |
3 |
4 |
D |
1 |
2 |
1 | |||||
|
В |
0,5 |
1 |
5 |
В |
0,333 |
1 |
2 |
В |
0,5 |
1 |
0,5 | |||||
|
С |
0,2 |
0,2 |
1 |
С |
0,25 |
0 |
1 |
С |
1 |
2 |
1 | |||||
Соответствующие нормализованные матрицы и весовые коэффициенты альтернатив:
|
Петров П.Е. | |||||
|
NDC= |
|
D |
В |
С |
wi |
|
D |
0,4 |
0,429 |
0,333 |
0,387 | |
|
В |
0,4 |
0,429 |
0,5 |
0,443 | |
|
С |
0,2 |
0,143 |
0,167 |
0,170 | |
|
NDК= |
|
D |
В |
С |
wi |
|
D |
0,545 |
0,571 |
0,5 |
0,539 | |
|
В |
0,273 |
0,286 |
0,333 |
0,297 | |
|
С |
0,182 |
0,143 |
0,167 |
0,164 | |
|
NDАр = |
|
А |
В |
С |
wi |
|
D |
0,286 |
0,286 |
0,286 |
0,286 | |
|
В |
0,143 |
0,143 |
0,143 |
0,143 | |
|
С |
0,571 |
0,571 |
0,571 |
0,571 | |
|
Иванов И.В. | |||||
|
NDC= |
|
D |
В |
С |
wi |
|
D |
0,632 |
0,571 |
0,667 |
0,623 | |
|
В |
0,158 |
0,143 |
0,111 |
0,137 | |
|
С |
0,211 |
0,286 |
0,222 |
0,239 | |
|
NDК= |
|
D |
В |
С |
wi |
|
D |
0,632 |
0,667 |
0,571 |
0,623 | |
|
В |
0,211 |
0,222 |
0,286 |
0,239 | |
|
С |
0,158 |
0,111 |
0,143 |
0,137 | |
|
NDАр= |
|
D |
В |
С |
wi |
|
D |
0,571 |
0,6 |
0,5 |
0,571 | |
|
В |
0,286 |
0,3 |
0,375 |
0,286 | |
|
С |
0,143 |
0,1 |
0,125 |
0,143 | |
|
Некрасов Н.Е. | |||||
|
NDC= |
|
D |
В |
С |
wi |
|
D |
0,588 |
0,625 |
0,455 |
0,556 | |
|
В |
0,294 |
0,313 |
0,455 |
0,354 | |
|
С |
0,118 |
0,063 |
0,091 |
0,090 | |
|
NDК= |
|
D |
В |
С |
wi |
|
D |
0,632 |
0,667 |
0,571 |
0,623 | |
|
В |
0,211 |
0,222 |
0,286 |
0,239 | |
|
С |
0,158 |
0,111 |
0,143 |
0,137 | |
|
NDАр= |
|
D |
В |
С |
wi |
|
D |
0,4 |
0,4 |
0,4 |
0,4 | |
|
В |
0,2 |
0,2 |
0,2 |
0,2 | |
|
С |
0,4 |
0,4 |
0,4 |
0,4 | |
Проверим согласованности матриц сравнений альтернатив.
Столбцы матрицы NDАр (Петров П.Е.) и NDАр (Некрасов Н.Е.) одинаковы. Это имеет место лишь в случае, когда лицо, принимающее решение, проявляет идеальную согласованность в определении элементов матрицы сравнений, т.е. матрица сравнений является согласованной.
Оценим уровень несогласованности остальных матриц сравнений.
Проверим согласованность матрицы сравнений альтернатив в рамках критерия «Спрос», составленную экспертом Петровым П.Е.
|
|
1 |
1 |
2 |
|
0,387 |
= |
1,170 |
|
1 |
1 |
3 |
0,443 |
1,340 | |||
|
0 |
0,333 |
1 |
0,170 |
0,511 |
Отсюда получаем: nmax = 3,021
Следовательно, для n=3 имеем:
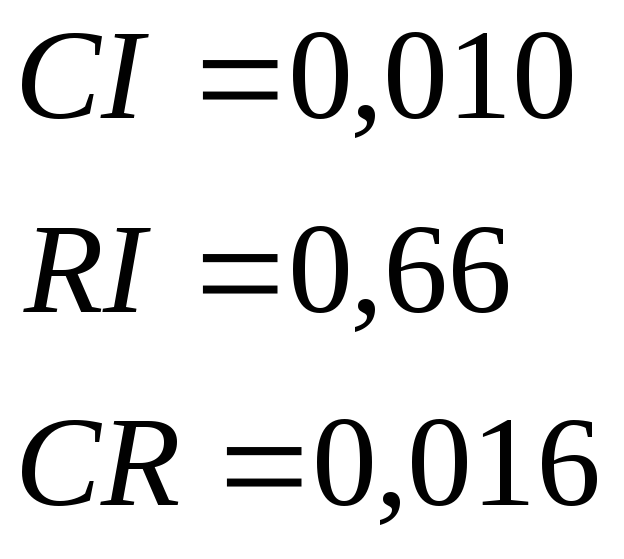
Так как CR<0,1, уровень несогласованности матрицы DС является приемлемым.
Проверим согласованность матрицы сравнений альтернатив в рамках критерия «Конкуренция», составленную экспертом Петровым П.Е.
|
|
1 |
2 |
3 |
|
0,539 |
= |
1,625 |
|
0,5 |
1 |
2 |
0,297 |
0,894 | |||
|
0,333 |
0,5 |
1 |
0,164 |
0,492 |
Отсюда получаем: nmax = 3,011
Следовательно, для n=3 имеем:

Так как CR<0,1, уровень несогласованности матрицы DК является приемлемым.
Проверим согласованность матрицы сравнений альтернатив в рамках критерия «Спрос», составленную экспертом Ивановым И.В.
|
|
1 |
4 |
3 |
|
0,623 |
= |
1,891 |
|
0,25 |
1 |
0,5 |
0,137 |
0,413 | |||
|
0,3333 |
2 |
1 |
0,239 |
0,722 |
Отсюда получаем: nmax = 3,025
Следовательно, для n=3 имеем:

Так как CR<0,1, уровень несогласованности матрицы DС является приемлемым.
Проверим согласованность матрицы сравнений альтернатив в рамках критерия «Конкуренция», составленную экспертом Ивановым И.В.
|
|
1 |
3 |
4 |
|
0,623 |
= |
1,891 |
|
0,333 |
1 |
2 |
0,239 |
0,722 | |||
|
0,25 |
0,5 |
1 |
0,137 |
0,413 |
Отсюда получаем: nmax = 3,025
Следовательно, для n=3 имеем:
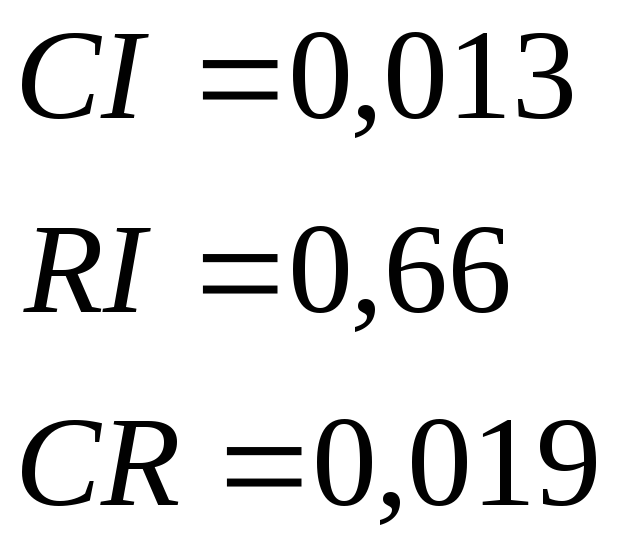
Так как CR<0,1, уровень несогласованности матрицы DК является приемлемым.
Проверим согласованность матрицы сравнений альтернатив в рамках критерия «Арендная плата», составленную экспертом Ивановым И.В.
|
|
1 |
2 |
4 |
|
0,557 |
= |
1,688 |
|
0,5 |
1 |
3 |
0,320 |
0,967 | |||
|
0,25 |
0,333 |
1 |
0,123 |
0,369 |
Отсюда получаем: nmax = 3,023
Следовательно, для n=3 имеем:
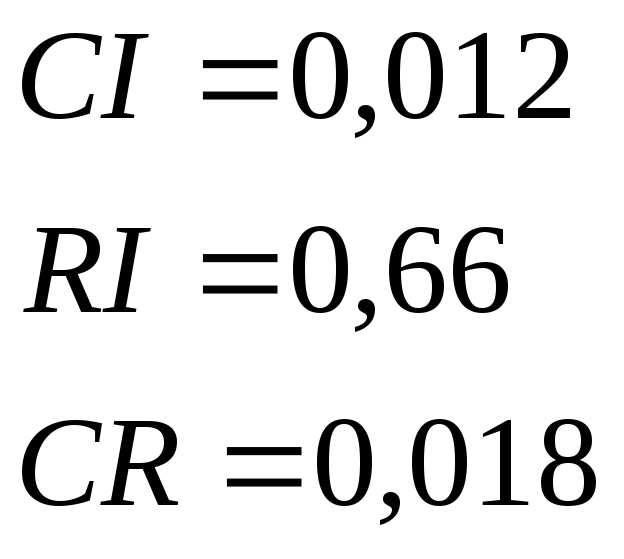
Так как CR<0,1, уровень несогласованности матрицы DАр является приемлемым.
Проверим согласованность матрицы сравнений альтернатив в рамках критерия «Спрос», составленную экспертом Некрасовым И.В.
|
|
1 |
2 |
5 |
|
0,090 |
= |
1,715 |
|
0,5 |
1 |
5 |
0,090 |
1,083 | |||
|
0,2 |
0,2 |
1 |
0,090 |
0,272 |
Отсюда получаем: nmax = 3,071
Следовательно, для n=3 имеем:
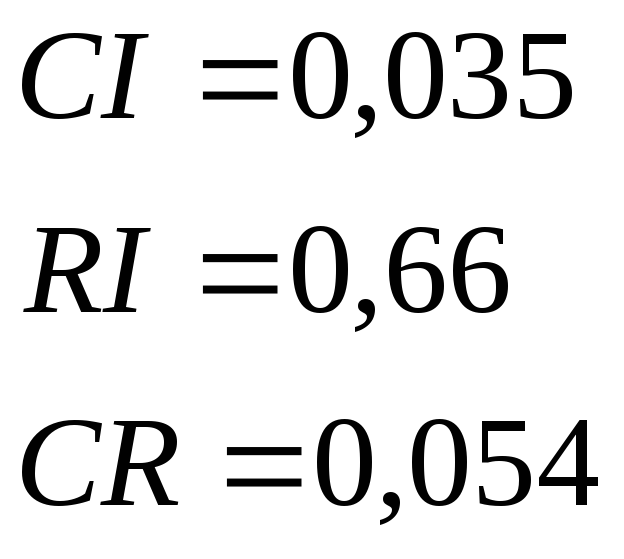
Так как CR<0,1, уровень несогласованности матрицы DС является приемлемым.
Проверим согласованность матрицы сравнений альтернатив в рамках критерия «Конкуренция», составленную экспертом Некрасовым И.В.
|
|
1 |
3 |
4 |
|
0,623 |
= |
1,891 |
|
0,333 |
1 |
2 |
0,239 |
0,722 | |||
|
0,25 |
0,5 |
1 |
0,137 |
0,413 |
Отсюда получаем: nmax = 3,025
Следовательно, для n=3 имеем:
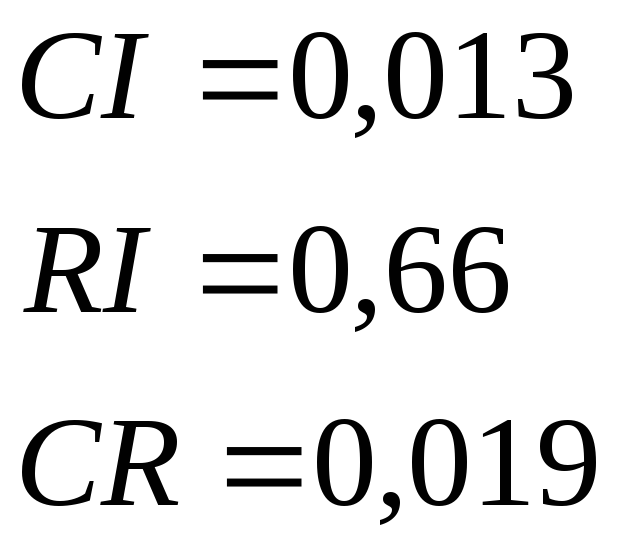
Так как CR<0,1, уровень несогласованности матрицы DК является приемлемым.
В результате мы имеем весовые коэффициенты альтернатив в соответствии с каждым критерием для каждого эксперта, которые представлены в Таблица 2.
Таблица 2
|
|
Петров П.Е. |
Иванов И.В. |
Некрасов Н.А. | ||||||
|
|
С |
К |
Ар |
С |
К |
Ар |
С |
К |
Ар |
|
D |
0,387 |
0,539 |
0,286 |
0,623 |
0,623 |
0,557 |
0,556 |
0,623 |
0,4 |
|
В |
0,443 |
0,297 |
0,143 |
0,137 |
0,239 |
0,320 |
0,354 |
0,239 |
0,2 |
|
С |
0,170 |
0,164 |
0,571 |
0,239 |
0,137 |
0,123 |
0,090 |
0,137 |
0,4 |
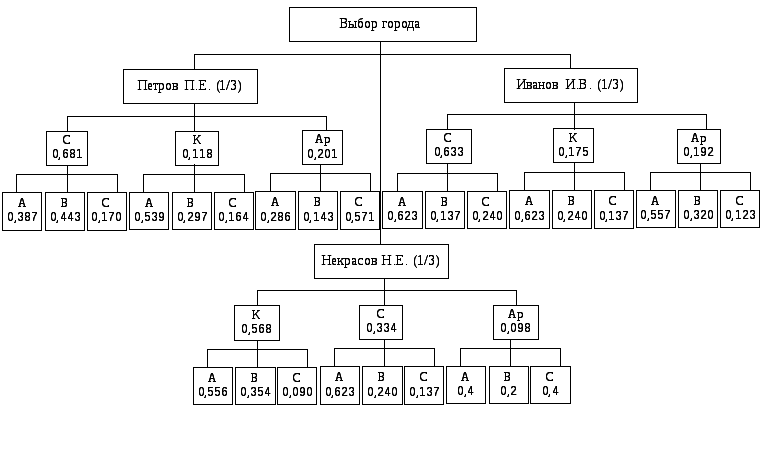
4. Полученные в результате расчетов данные ( Таблица 1 и Таблица 2) для наглядности представим на дереве (Рисунок 1).
Комбинированный вес W для каждого города определяется по единой схеме. Например, для города D можно записать:
 .
.
Таким образом, в результате проведенных вычислений получаем следующие комбинированные весовые коэффициенты для каждого из городов:
|
WD= |
0,519 |
|
WB = |
0,285 |
|
WC = |
0,195 |
В результате, город D получает наивысший комбинированный вес и, следовательно, является наиболее оптимальным выбором для размещения склада.
Рисунок 1