5.3.3 Решение матричных игр методами линейного программирования

Представленные выше примеры решение игры со смешенными стратегиями наглядно иллюстрируют теоретические положения матричных игр и трудоемкость ручного счета даже при матрице 2х2. Для авоматизации расчетов можно использовать программные продукты , метод расчета в которых основан на решении системы линейных уравнений http://www.uchimatchast.ru/.

Любую конечную игру двух лиц с нулевой суммой можно представить в виде задачи линейного программирования. При этом возможно решение задачи как с чистыми так со смешенными стратегиями. В случае чистых стратегий вероятность одной из стратегий будет равна единице, а вероятность остальных стратегий ,естественно, равна нулю.

Оптимальные значения вероятностей стратегийигрока А могут быть определены путем решения следующей максиминной задачи.

Сформулируем задачу матричной игры. Две конкурирующие компании А и B выпускают продукцию. Для увеличения продаж товар поставляется в различных упаковках. Компания А использует картон А₁, целлофан А₂, пластмасс А₃. Компания B использует такие же материалы для упаковки. Однако, при этом компании использовали различные виды оформления упаковок. В компании А зафиксировали увеличение/уменьшение притока покупателей в зависимости от упаковки товара и стратегии поведения конкурента B. Эти статистические данные представлены в таблице.

	В1	В2	В3	Мин строк
А1	3	-2	-3	-3
А2	-2	4	-1	-2
А3	-3	-6	2	-6
Макс столбцов	3	4	2

Решение задачи основано на получение наилучшего результата из наихудших для каждого игрока, который может быть получен определенной стратегии поведения. Из представленной таблицы следует, что данную задачу нельзя решить на основе чистых стратегий (седловой точки нет). Решение задачи находится между -2 и 2. В данном случае присутствуют смешенные стратегии, а так как количество стратегий у игрока А равно трем эту задачу можно решить с помощью линейного программирования (ЛП) алгебраическим методом. Следует заметить, что эту задачу нельзя решить графическим методом, так как количество стратегий у каждого игрока больше двух.

В соответствии с данными, представленными в таблице, задача ЛП для игрока А записывается следующим образом

максимизировать: (максимальное количество клиентов) при выполнении следующих ограничений:

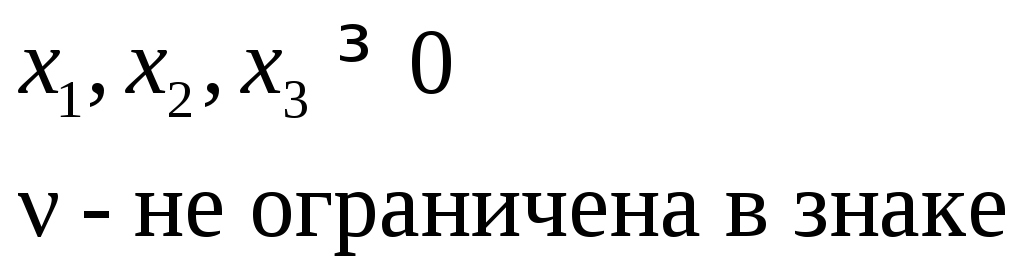
5.3.3.1 Решение задачи лп симплекс-методом

Приведем систему ограничений к каноническому виду, для этого необходимо неравенства преобразовать в равенства, с добавлением дополнительных переменных. Если в преобразуемом неравенстве стоит знак ≥, то при переходе к равенству знаки всех его коэффициентов и свободных членов меняются на противоположные. Тогда система запишется в виде:

Переходим к формированию исходной симплекс таблицы. В строку F таблицы заносятся коэффициенты целевой функции. Так как нам необходимо найти максимум целевой функции, то в таблицу заносятся коэффициенты с противоположным знаком

Так как среди исходного набора условий были равенства, мы ввели искусственные переменные R. Это значит, что в симплекс таблицу нам необходимо добавить дополнительную строку M, элементы которой рассчитываются как сумма соответствующих элементов условий-равенств (тех которые после приведения к каноническому виду содержат искусственные переменные R) взятая с противоположным знаком.

Из данных задачи составляем исходную симплекс таблицу.

	x1	x2	x3	x4	x5	x6	x7	x8	Свободный член
F	-1	1	0	0	0	0	0	0	0
x9	1	-1	-3	2	3	1	0	0	0
x10	1	-1	2	-4	6	0	1	0	0
x11	1	-1	3	1	-2	0	0	1	0
R1	0	0	1	1	1	0	0	0	1
M	0	0	-1	-1	-1	0	0	0	-1

Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение. В строке M имеются отрицательные элементы, это означает что полученное решение не оптимально. Определим ведущий столбец. Для этого найдем в строке M максимальный по модулю отрицательный элемент - это -1 Ведущей строкой будет та, для которой отношение свободного члена к соответствующему элементу ведущего столбца минимально. Ведущей строкой является R₁, а ведущий элемент: 1.

	x1	x2	x4	x5	x6	x7	x8	Свободный член
F	-1	1	0	0	0	0	0	0
x9	1	-1	5	6	0	0	0	3
x10	1	-1	-6	4	1	0	0	-2
x11	1	-1	-2	-5	0	1	1	-3
x3	0	0	1	1	0	0	0	1
M	0	0	0	0	0	0	0	0

В составленной нами таблице имеются отрицательные элементы в столбце свободных членов, находим среди них максимальный по модулю - это элемент: -3, он задает ведущую строку - X₁₁. В этой строке так же находим максимальный по модулю отрицательный элемент: -5 он находится в столбце X₅, который будет ведущим столбцом. Переменная в ведущей строке исключается из базиса, а переменная соответствующая ведущему столбцу включается в базис. Пересчитаем симплекс-таблицу:

	x1	x2	x4	x11	x6	x7	x8	Свободный член
F	-1	1	0	0	0	0	0	0
x9	2,2	-2,2	2,6	1,2	1	0	1,2	-0,6
x10	1,8	-1,8	-7,6	0,8	0	1	0,8	-4,4
x5	-0,2	0,2	0,4	-0,2	0	0	-0,2	0,6
x3	0,2	-0,2	0,6	0,2	0	0	0,2	0,4
M	0	0	0	0	0	0	0	0

В составленной нами таблице имеются отрицательные элементы в столбце свободных членов, находим среди них максимальный по модулю - это элемент: -4,4, он задает ведущую строку - X₁₀. В этой строке так же находим максимальный по модулю отрицательный элемент: -7,6 он находится в столбце X₄, который будет ведущим столбцом. Переменная в ведущей строке исключается из базиса, а переменная соответствующая ведущему столбцу включается в базис. Пересчитаем симплекс-таблицу:

	x1	x2	x 10	x11	x6	x7	x8	Свободный член
F	-1	1	-0	0	0	0	0	0
x9	2,82	-2,82	0,34	1,47	1	0,34	1,47	-2,11
x4	-0,24	0,24	-0,13	-0,11	-0	-0,13	-0,11	0,58
x5	-0,11	0,11	0,05	-0,16	0	0,05	-0,16	0,37
x3	0,34	-0,34	0,08	0,26	0	0,08	0,26	0,05
M	0	0	0	0	0	0	0	0

В составленной нами таблице имеются отрицательные элементы в столбце свободных членов, находим среди них максимальный по модулю - это элемент: -2,11, он задает ведущую строку - X₉. В этой строке так же находим максимальный по модулю отрицательный элемент: - 2,82 он находится в столбце X₂, который будет ведущим столбцом. Переменная в ведущей строке исключается из базиса, а переменная соответствующая ведущему столбцу включается в базис. Пересчитаем симплекс-таблицу:

	x1	x9	x 10	x11	x6	x7	x8	Свободный член
F	0	0,35	0,12	0,52	0,35	0,12	0,52	-0,75
x2	-1	-0,35	-0,12	-0,52	-0,35	-0,12	-0,52	0,75
x4	0	0,09	-0,1	0,02	0,09	-0,1	0,02	0,4
x5	0	0,04	0,06	-0,1	0,04	0,06	-0,1	0,29
X3	0	-0,12	0,04	0,08	-0,12	0,04	0,08	0,3
M	0	-0	0	0	0	0	0	0

Так как в строке F нет отрицательных элементов, то найдено оптимальное решение F=-0,75 при значениях переменных равных: X₂=0,75, X₄=0,4, X₅=0,29, X₃=0,3.

В соответствии с данными, представленными в таблице, задача ЛП для игрока B записывается следующим образом:

максимизировать: (минимальное количество клиентов) при выполнении следующих ограничений:

Приведем систему ограничений к каноническому виду, для этого необходимо неравенства преобразовать в равенства, с добавлением дополнительных переменных.

Если в преобразуемом неравенстве стоит знак ≥, то при переходе к равенству знаки всех его коэффициентов и свободных членов меняются на противоположные.

Тогда система запишется в виде:

Переходим к формированию исходной симплекс таблицы. В строку F таблицы заносятся коэффициенты целевой функции.

Так как среди исходного набора условий были равенства, мы ввели искусственные переменные R. Это значит, что в симплекс таблицу нам необходимо добавить дополнительную строку M, элементы которой рассчитываются как сумма соответствующих элементов условий-равенств (тех которые после приведения к каноническому виду содержат искусственные переменные R) взятая с противоположным знаком.

Из данных задачи составляем исходную симплекс таблицу.

	x1	x2	x2	x3	x4	x5	x6	x7	Свободный член
F	1	-1	0	0	0	0	0	0	0
x9	-1	1	3	-2	-3	1	0	0	0
x10	-1	1	-2	4	-1	0	1	0	0
x11	-1	1	-3	-6	2	0	0	1	0
R1	0	0	1	1	1	0	0	0	1
M	0	0	-1	-1	-1	0	0	0	-1

Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение. В строке M имеются отрицательные элементы, это означает что полученное решение не оптимально. Определим ведущий столбец. Для этого найдем в строке M максимальный по модулю отрицательный элемент - это -1. Ведущей строкой будет та, для которой отношение свободного члена к соответствующему элементу ведущего столбца минимально. Ведущей строкой является R₁, а ведущий элемент: 1.

	x1	x2	x4	x5	x6	x7	x8	Свободный член
F	1	-1	0	0	0	0	0	0
x9	-1	1	-5	-6	1	0	0	-3
x10	-1	1	6	1	0	1	0	2
x11	-1	1	-3	5	0	0	1	3
x3	0	0	1	1	0	0	0	1
M	0	0	0	0	0	0	0	0

В составленной нами таблице имеются отрицательные элементы в столбце свободных членов, находим среди них максимальный по модулю - это элемент: -3, он задает ведущую строку - X₉. В этой строке так же находим максимальный по модулю отрицательный элемент: -6 он находится в столбце X₅, который будет ведущим столбцом. Переменная в ведущей строке исключается из базиса, а переменная соответствующая ведущему столбцу включается в базис. Пересчитаем симплекс-таблицу:

	x1	x2	x4	x9	x6	x7	x8	Свободный член
F	1	-1	0	0	0	0	0	0
x5	0,17	-0,17	0,83	-0,17	-0,17	0	0	0,5
x10	-1,17	1,17	5,17	0,17	0,17	1	0	1,5
x11	-1,83	1,83	-7,17	0,83	0,83	0	1	0,5
X3	-0,17	0,17	0,17	0,17	0,17	0	0	0,5
M	0	0	0	0	0	0	0	0

В строке M отрицательные элементы отсутствуют. Рассмотрим строку F в которой имеются отрицательные элементы, это означает что полученное решение не оптимально. Определим ведущий столбец. Для этого найдем в строке F максимальный по модулю отрицательный элемент - это -1. Ведущей строкой будет та, для которой положительное отношение свободного члена к соответствующему элементу ведущего столбца минимально. Ведущей строкой является X₁₁, а ведущий элемент: 1,83.

	x1	x11	x4	x9	x6	x7	x8	Свободный член
F	0	0,55	-3,92	0,45	0,45	0	0,55	0,27
x5	0	0,09	0,16	-0,09	-0,09	0	0,09	0,55
x10	0	-0,64	9,75	-0,36	-0,36	1	-0,64	1,18
x2	-1	0,55	-3,92	0,45	0,45	0	0,55	0,27
x3	0	-0,09	0,84	0,09	0,09	0	-0,09	0,45
M	0	0	0	0	0	0	0	0

В строке M отрицательные элементы отсутствуют. Рассмотрим строку F в которой имеются отрицательные элементы, это означает что полученное решение не оптимально. Определим ведущий столбец. Для этого найдем в строке F максимальный по модулю отрицательный элемент - это -3,92. Ведущей строкой будет та для которой положительное отношение свободного члена к соответствующему элементу ведущего столбца минимально. Ведущей строкой является X₁₀, а ведущий элемент: 9,75.

	x1	x11	x10	x9	x6	x7	x8	Свободный член
F	0	0,29	0,4	0,31	0,31	0,4	0,29	0,75
x5	0	0,1	-0,02	-0,09	-0,09	-0,02	0,1	0,53
x4	0	-0,07	0,1	-0,04	-0,04	0,1	-0,07	0,12
x2	-1	0,29	0,4	0,31	0,31	0,4	0,29	0,75
x3	0	-0,04	-0,09	0,12	0,12	-0,09	-0,04	0,35
M	0	0	0	0	0	0	0	0

Так как в строке F нет отрицательных элементов, то найдено оптимальное решение. Так как исходной задачей был поиск минимума, оптимальное решение есть свободный член строки F, взятый с противоположным знаком. Найдено оптимальное решение F=-0.75 при значениях переменных равных: X₅=0,53, X₄=0,12, X₂=0,75, X₃=0,35.

Проведенный расчет показал. Значение игры, как со стороны игрока А, так и со стороны игрока B одинакова и равняется -0,75.