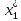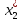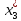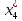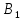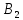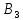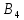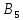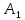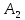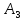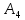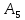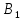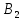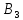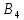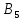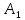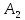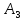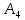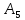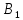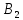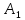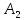Решение:
|
|
g1(x) |
g2(x) |
g3(x) |
g4(x) |
|
0 |
0 |
0 |
0 |
0 |
|
50 |
13 |
63 |
101 |
17 |
|
100 |
23 |
78 |
125 |
19 |
|
150 |
43 |
89 |
128 |
21 |
|
200 |
58 |
96 |
132 |
24 |
Пусть
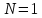 ,
тогда
,
тогда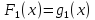
Пусть
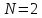 ,
тогда
,
тогда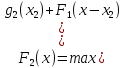
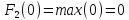
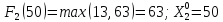
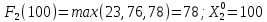
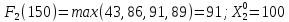
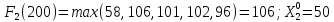
Пусть
 ,
тогда
,
тогда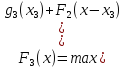
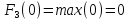
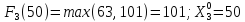
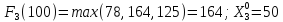
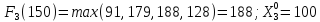
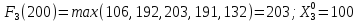
Пусть
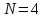 ,
тогда
,
тогда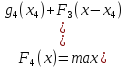
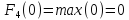
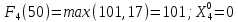
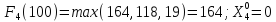
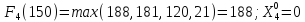
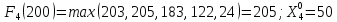
|
|
F1(x) |
F2(x) |
F3(x) |
F4(x) |
|
0 |
0 |
0 |
0 |
0 |
|
50 |
13 |
63 |
101 |
101 |
|
100 |
23 |
78 |
164 |
164 |
|
150 |
43 |
91 |
188 |
188 |
|
200 |
58 |
106 |
203 |
205 |
Оптимальный план распределения между 4 предприятиями 200 тыс.р. капиталовложений:
|
|
|
|
|
|
0 |
50 |
100 |
50 |
Второму предприятию – 50 тыс.р.
Третьему предприятию – 100 тыс.р.
Четвертому предприятию – 50 тыс.р.
При этом суммарный прирост прибыли достигнет максимальной величины, равной 205.
Задача 6
N1
Дана платежная матрица 5х5 для двух банков.
Определить нижнюю и верхнюю цены игры и соответствующие им минимальные и максимальные стратегии.
|
|
|
|
|
|
|
|
|
4 |
-1 |
5 |
2 |
7 |
|
|
1 |
2 |
3 |
4 |
-5 |
|
|
7 |
3 |
8 |
-3 |
6 |
|
|
2 |
4 |
9 |
5 |
2 |
|
|
-3 |
6 |
1 |
8 |
9 |
Найдем чистые нижнюю и верхнюю цены игры.
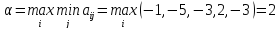
Нижняя цена
соответствует стратегии
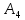 1-го игрока
1-го игрока
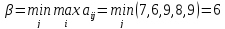
Верхняя цена игры
соответствует стратегии
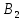 2-го игрока.
2-го игрока.
N2
Дана платежная матрица 5×5 для двух банков. Определить чистую цену игры и соответствующие стратегии банков А и В.
|
|
|
|
|
|
|
|
|
5 |
-1 |
8 |
4 |
2 |
|
|
-3 |
5 |
2 |
6 |
4 |
|
|
4 |
3 |
1 |
7 |
-2 |
|
|
8 |
10 |
9 |
11 |
13 |
|
|
6 |
4 |
5 |
-3 |
7 |
Найдем чистые нижнюю и верхнюю цены игры.
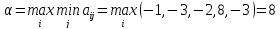
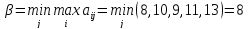
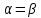 –чистая цена игры
равна 8
–чистая цена игры
равна 8
Соответствующие
стратегии банков
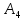 и
и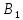
N3
Дана платежная матрица 2×2 для двух банков.
Определить
оптимальные смешанные стратегии банков
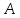 и
и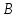 (т.е. определить цену игры
(т.е. определить цену игры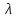 и соответствующие вероятности оптимальных
стратегий).
и соответствующие вероятности оптимальных
стратегий).
|
|
|
|
|
|
5 |
13 |
|
|
12 |
9 |
Решение:
Проверим наличие седловой точки:
Найдем чистые нижнюю и верхнюю цены игры.
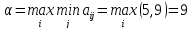
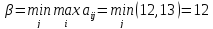
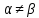 , поэтому задача
неразрешима в чистых стратегиях.
, поэтому задача
неразрешима в чистых стратегиях.
Составим ЗЛП для каждого игрока:
Для 1-го игрока- найти минимальное значение функции:
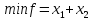
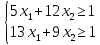
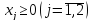
Для 2-го игрока - найти максимальное значение функции:
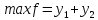
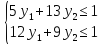
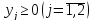
Вводя вспомогательные
переменные
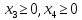 для исходной задачи и
для исходной задачи и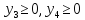 для двойственной,
модели задач преобразуем к канонической
форме. При этом вспомогательные переменные
примем за базисные. Соответствие между
переменными пары взаимно двойственных
задач будет следующим:
для двойственной,
модели задач преобразуем к канонической
форме. При этом вспомогательные переменные
примем за базисные. Соответствие между
переменными пары взаимно двойственных
задач будет следующим:
|
x1 |
x2 |
x3 |
x4 |
|
|
|
|
|
|
y3 |
y4 |
y1 |
y2 |
Приведем задачу к каноническому виду. Введем дополнительные переменные. В целевую функцию все дополнительные переменные введем с коэффициентом, равным нулю. Дополнительные переменные прибавим к левым частям ограничений, не имеющих предпочтительного вида, и получим равенства.
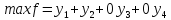
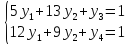
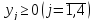
Заполняем симплексную таблицу:
|
№ |
БП |
cБ |
Ao |
y1 |
y2 |
y3 |
y4 |
Симплексные |
|
|
|
|
|
1 |
1 |
0 |
0 |
отношения |
|
0 |
y3 |
0 |
1 |
5 |
13 |
1 |
0 |
1/5 |
|
|
y4 |
0 |
1 |
12 |
9 |
0 |
1 |
1/12 |
|
|
fj - cj |
0 |
-1 |
-1 |
0 |
0 |
| |
|
1 |
y3 |
0 |
7/12 |
0 |
37/4 |
1 |
-5/12 |
7/111 |
|
|
y1 |
1 |
1/12 |
1 |
3/4 |
0 |
1/12 |
1/9 |
|
|
fj - cj |
1/12 |
0 |
-1/4 |
0 |
1/12 |
| |
|
2 |
y2 |
1 |
7/111 |
0 |
1 |
4/37 |
-5/111 |
|
|
|
y1 |
1 |
4/111 |
1 |
0 |
-3/37 |
13/111 |
|
|
|
fj - cj |
11/111 |
0 |
0 |
1/37 |
8/111 |
| |
На основании симплексной таблицы получено следующее решение задачи линейного программирования:
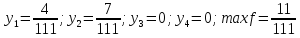
На основании симплексной таблицы получено следующее решение двойственной задачи линейного программирования:
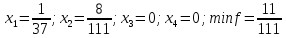
По формулам:
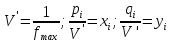
Получим цену игры:
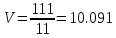
и вероятности
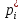 и
и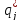 для оптимальных смешанных стратегий
соответственно для 1-го и в 2-го игрока:
для оптимальных смешанных стратегий
соответственно для 1-го и в 2-го игрока:
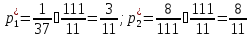
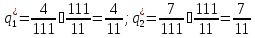

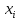 ,
тыс.р.
,
тыс.р.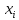 ,
тыс.р.
,
тыс.р.