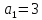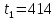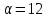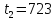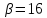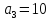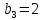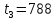Задача 1
Предположим, что
для производства двух видов продукции
 и
и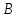 можно использовать только материал
трех сортов. При этом на изготовление
единицы изделия вида
можно использовать только материал
трех сортов. При этом на изготовление
единицы изделия вида расходуется
расходуется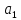 кг материала первого сорта,
кг материала первого сорта,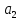 кг материала второго сорта и
кг материала второго сорта и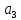 кг материала третьего сорта. На
изготовление единицы изделия вида
кг материала третьего сорта. На
изготовление единицы изделия вида расходуется
расходуется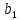 кг материала первого сорта,
кг материала первого сорта, кг материала второго сорта,
кг материала второго сорта,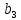 кг материала третьего сорта. На складе
фабрики имеется всего материала первого
сорта
кг материала третьего сорта. На складе
фабрики имеется всего материала первого
сорта кг, материала второго сорта
кг, материала второго сорта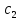 кг, материала третьего сорта
кг, материала третьего сорта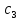 кг. От реализации единицы готовой
продукции вида
кг. От реализации единицы готовой
продукции вида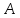 фабрика имеет прибыль
фабрика имеет прибыль руб., а от продукции вида
руб., а от продукции вида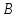 прибыль составила
прибыль составила руб.
руб.
Определить
максимальную прибыль от реализации
всей продукции видов
 и
и .
Решить задачу симплекс-методом. Дать
геометрическую интерпретацию
математической формулировки задачи.
.
Решить задачу симплекс-методом. Дать
геометрическую интерпретацию
математической формулировки задачи.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Через
 и
и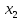 обозначим количество производимых
изделий вида
обозначим количество производимых
изделий вида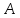 и
и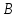 соответственно. Тогда целевая функция
экономико-математической модели,
выражающая получаемую прибыль:
соответственно. Тогда целевая функция
экономико-математической модели,
выражающая получаемую прибыль:
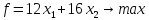
Неравенства-ограничения на используемое сырье:
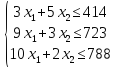
По смыслу задачи
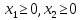
Получаем следующую экономико-математическую модель:
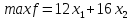
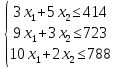
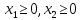
Приведем задачу к каноническому виду. Введем дополнительные переменные. В целевую функцию все дополнительные переменные введем с коэффициентом, равным нулю. Дополнительные переменные прибавим к левым частям ограничений, не имеющих предпочтительного вида, и получим равенства.
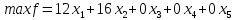
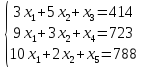
Заполняем симплексную таблицу:
|
№ |
БП |
cБ |
Ao |
x1 |
x2 |
x3 |
x4 |
x5 |
Симплексные |
|
|
|
|
|
12 |
16 |
0 |
0 |
0 |
отношения |
|
0 |
x3 |
0 |
414 |
3 |
5 |
1 |
0 |
0 |
414/5 |
|
|
x4 |
0 |
723 |
9 |
3 |
0 |
1 |
0 |
241 |
|
|
x5 |
0 |
788 |
10 |
2 |
0 |
0 |
1 |
394 |
|
|
fj - cj |
0 |
-12 |
-16 |
0 |
0 |
0 |
| |
|
1 |
x2 |
16 |
414/5 |
3/5 |
1 |
1/5 |
0 |
0 |
138 |
|
|
x4 |
0 |
2373/5 |
36/5 |
0 |
-3/5 |
1 |
0 |
791/12 |
|
|
x5 |
0 |
3112/5 |
44/5 |
0 |
-2/5 |
0 |
1 |
778/11 |
|
|
fj - cj |
6624/5 |
-12/5 |
0 |
16/5 |
0 |
0 |
| |
|
2 |
x2 |
16 |
173/4 |
0 |
1 |
1/4 |
-1/12 |
0 |
|
|
|
x1 |
12 |
791/12 |
1 |
0 |
-1/12 |
5/36 |
0 |
|
|
|
x5 |
0 |
127/3 |
0 |
0 |
1/3 |
-11/9 |
1 |
|
|
|
fj - cj |
1483 |
0 |
0 |
3 |
1/3 |
0 |
| |
На основании симплексной таблицы получено следующее решение задачи линейного программирования:

Таким образом,
необходимо выпускать 65.9 изделий вида
 и 43.3 изделий вида
и 43.3 изделий вида .
Прибыль достигнет максимума и составит
1483 ден.ед. При реализации оптимального
плана остаток ресурса 3-го вида составит
42.3 единиц.
.
Прибыль достигнет максимума и составит
1483 ден.ед. При реализации оптимального
плана остаток ресурса 3-го вида составит
42.3 единиц.
Дадим геометрическую интерпретацию решения.
Для построения области допустимых решений строим в системе координат соответствующие данным ограничениям-неравенствам граничные прямые:
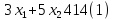

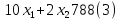
Строим вектор
 ,
координаты которого пропорциональны
коэффициентам целевой функции. Здесь
,
координаты которого пропорциональны
коэффициентам целевой функции. Здесь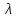 -
коэффициент пропорциональности.
-
коэффициент пропорциональности.
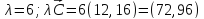
Перпендикулярно
к построенному вектору проводим линию
уровня
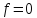 .
.
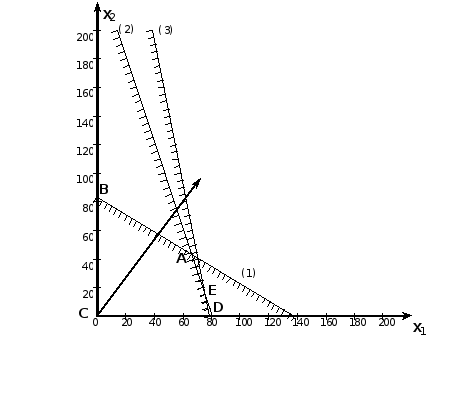
Областью допустимых
решений является фигура
 .
.
Перемещаем линию
уровня
 в направлении вектора так, чтобы она
касалась области допустимых решений в
крайней точке. Решением на максимум
является точка
в направлении вектора так, чтобы она
касалась области допустимых решений в
крайней точке. Решением на максимум
является точка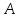 ,
координаты которой находим как точку
пересечения прямых (1) и (2).
,
координаты которой находим как точку
пересечения прямых (1) и (2).
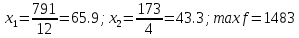
Таким образом,
необходимо выпускать 65.9 изделий вида
 и 43.3 изделий вида
и 43.3 изделий вида .
Прибыль достигнет максимума и составит
1483 ден.ед.
.
Прибыль достигнет максимума и составит
1483 ден.ед.